Das vertraute rechteckige Gitter ist ein einfaches System zum Lernen, aber es ist nicht in allen Situationen bequem. Was, wenn Sie die Speichen auf einem Rad oder die Bewegung von Wasser in einem Abfluss planen wollen? In diesen Fällen ist ein kreisförmiges Koordinatensystem natürlicher. Sie haben die Grundidee der Polarkoordinaten bereits im Alltag genutzt.[1] Wenn Sie zum Beispiel die Quelle einer Sirene suchen, benötigen Sie zwei Informationen: Wie weit ist es entfernt und aus welcher Richtung kommt der Ton? Das Polarkoordinatensystem mappt auf die gleiche Weise und beschreibt die Entfernung von einem festen Punkt und dem Winkel von einem festen Strahl.
Teil eins von vier:
Plotten von Polarkoordinaten
-
 1 Richte die Polarebene ein. Sie haben wahrscheinlich zuvor Punkte mit kartesischen Koordinaten grafisch dargestellt Notation, um Orte auf einem rechteckigen Gitter zu markieren. Polarkoordinaten verwenden stattdessen eine andere Art von Graphen, basierend auf Kreisen:[2]
1 Richte die Polarebene ein. Sie haben wahrscheinlich zuvor Punkte mit kartesischen Koordinaten grafisch dargestellt Notation, um Orte auf einem rechteckigen Gitter zu markieren. Polarkoordinaten verwenden stattdessen eine andere Art von Graphen, basierend auf Kreisen:[2] - Der Mittelpunkt des Graphen (oder "Ursprung" in einem rechteckigen Raster) ist der Pole. Sie können dies mit dem Buchstaben O kennzeichnen.
- Ausgehend vom Pol, zeichne eine horizontale Linie nach rechts. Dies ist das polare Achse. Beschriften Sie die Achse mit Einheiten wie die positive x-Achse in einem rechteckigen Raster.
- Wenn Sie ein spezielles Polar-Graph-Papier haben, wird es viele Kreise unterschiedlicher Größe enthalten, die alle auf dem Pol zentriert sind. Sie müssen diese nicht selbst zeichnen, wenn Sie leeres Papier verwenden.
-
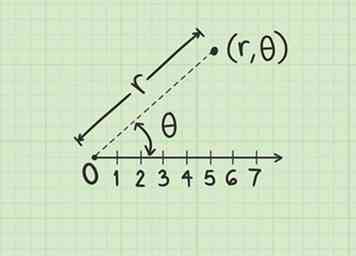 2 Verstehen Sie Polarkoordinaten. Auf der polaren Ebene wird ein Punkt durch eine Koordinate in der Form dargestellt :
2 Verstehen Sie Polarkoordinaten. Auf der polaren Ebene wird ein Punkt durch eine Koordinate in der Form dargestellt : - Die erste Variable, , steht für Radius. Der Punkt befindet sich auf einem Kreis mit Radius , zentriert auf dem Pol (Ursprung).
- Die zweite Variable, , repräsentiert einen Winkel. Der Punkt befindet sich entlang einer Linie, die durch den Pol verläuft und einen Winkel bildet mit der polaren Achse.
-
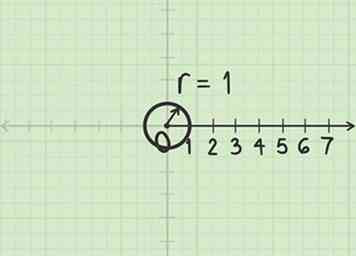 3 Überprüfen Sie den Einheitenkreis. In Polarkoordinaten wird der Winkel normalerweise im Bogenmaß anstatt in Grad gemessen. In diesem System deckt eine volle Drehung (360º oder ein voller Kreis) einen Winkel von 2 ab Radiant. (Dieser Wert wird gewählt, weil ein Kreis mit Radius 1 einen Umfang von 2 hat.) Wenn Sie sich mit dem Einheitskreis vertraut machen, wird das Arbeiten mit Polarkoordinaten viel einfacher.
3 Überprüfen Sie den Einheitenkreis. In Polarkoordinaten wird der Winkel normalerweise im Bogenmaß anstatt in Grad gemessen. In diesem System deckt eine volle Drehung (360º oder ein voller Kreis) einen Winkel von 2 ab Radiant. (Dieser Wert wird gewählt, weil ein Kreis mit Radius 1 einen Umfang von 2 hat.) Wenn Sie sich mit dem Einheitskreis vertraut machen, wird das Arbeiten mit Polarkoordinaten viel einfacher. - Wenn Ihr Lehrbuch Grade verwendet, brauchen Sie sich vorerst keine Gedanken darüber zu machen. Es ist möglich, Polarpunkte mit Gradwerten für .
Teil zwei von vier:
Einen Punkt zeichnen
-
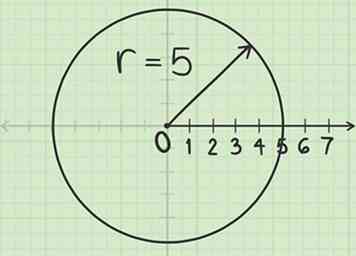 1 Konstruiere einen Kreis mit Radius . Irgendein Punkt hat Polarkoordinaten in der Form . Beginnen Sie mit dem Zeichnen eines Kreises mit Radius , zentriert auf dem Pol.
1 Konstruiere einen Kreis mit Radius . Irgendein Punkt hat Polarkoordinaten in der Form . Beginnen Sie mit dem Zeichnen eines Kreises mit Radius , zentriert auf dem Pol. - Der Pol ist der Mittelpunkt des Graphen, wo der Ursprung auf der rechtwinkligen Koordinatenebene liegt.
- Zum Beispiel, um den Punkt zu zeichnen Lege deinen Kompass auf die Stange. Erweitere das Bleistiftende des Kompasses um 5 Einheiten entlang der Polarachse. Drehen Sie den Kompass, um einen Kreis zu zeichnen.
-
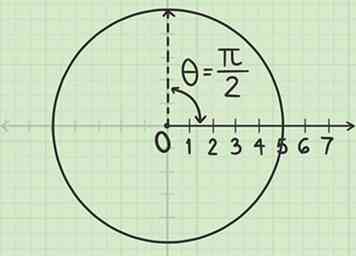 2 Messen Sie einen Winkel von von der polaren Achse. Platziere einen Winkelmesser, so dass die Mitte auf dem Pol liegt und die Kante entlang der Polarachse verläuft. Miss den Winkel von dieser Achse. Wenn der Winkel im Bogenmaß ist und Ihr Winkelmesser nur Grad anzeigt, können Sie die Einheiten umrechnen oder auf den Einheitskreis verweisen, um Hilfe zu erhalten.
2 Messen Sie einen Winkel von von der polaren Achse. Platziere einen Winkelmesser, so dass die Mitte auf dem Pol liegt und die Kante entlang der Polarachse verläuft. Miss den Winkel von dieser Achse. Wenn der Winkel im Bogenmaß ist und Ihr Winkelmesser nur Grad anzeigt, können Sie die Einheiten umrechnen oder auf den Einheitskreis verweisen, um Hilfe zu erhalten. - Für den Punkt Das sagt dir der Einheitskreis ist ¼ des Weges um den Kreis herum, was 90 Grad von der Polarachse entspricht.
- Messen Sie immer positive Winkel gegen den Uhrzeigersinn von der Achse. Miss negative Winkel im Uhrzeigersinn von der Achse.
-
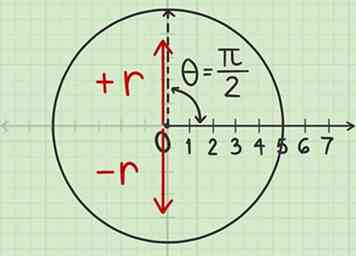 3 Zeichnen Sie eine Linie basierend auf dem Vorzeichen von . Der nächste Schritt wird sein, eine Linie entlang des von Ihnen gemessenen Winkels zu zeichnen. Bevor Sie dies jedoch tun können, müssen Sie wissen, auf welche Weise die Linie gezeichnet werden soll. Zurück zu den Polarkoordinaten herausfinden:
3 Zeichnen Sie eine Linie basierend auf dem Vorzeichen von . Der nächste Schritt wird sein, eine Linie entlang des von Ihnen gemessenen Winkels zu zeichnen. Bevor Sie dies jedoch tun können, müssen Sie wissen, auf welche Weise die Linie gezeichnet werden soll. Zurück zu den Polarkoordinaten herausfinden: - Ob Ist positiv, ziehe die Linie "vorwärts", von der Stange gerade durch die Winkelmarkierung, die du gerade gemacht hast.
- Ob ist negativ, ziehe die Linie "rückwärts": von der Winkelmarkierung zurück durch den Pol, um den Kreis auf der gegenüberliegenden Seite zu schneiden.
- Nicht durch rechtwinklige Koordinaten verwechselt werden: Dies entspricht nicht positiven oder negativen Werten auf einem x- oder y- Achse.
-
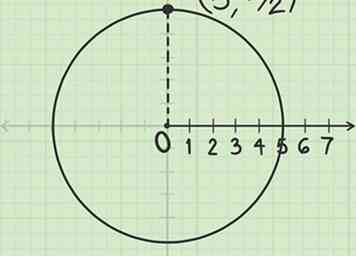 4 Beschriften Sie den Punkt, an dem sich die Linie und der Kreis treffen. Das ist der Punkt .
4 Beschriften Sie den Punkt, an dem sich die Linie und der Kreis treffen. Das ist der Punkt . - Die Stelle befindet sich auf einem Kreis mit dem Radius 5, der auf dem Pol zentriert ist, ¼ des Weges entlang des Kreisumfangs im Gegenuhrzeigersinn von der Polarachse. (Dieser Punkt entspricht (0, 5) in rechtwinkligen Koordinaten.)
Teil drei von vier:
Beispiele
Erstes Beispiel
Zeichnen Sie den Punkt P bei auf der polaren Ebene
-
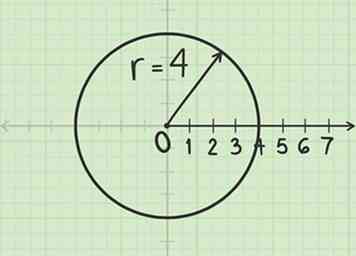 1 Konstruiere einen Kreis mit Radius . Verwenden Sie den Pfosten als Mittelpunkt.
1 Konstruiere einen Kreis mit Radius . Verwenden Sie den Pfosten als Mittelpunkt. -
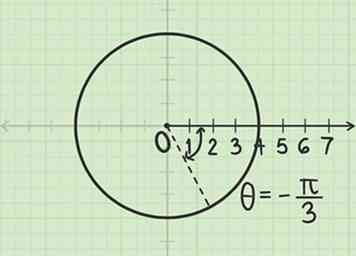 2 Miss den Winkel Radiant. Messen Sie diesen Winkel von der Polarachse (entspricht der positiven x-Achse). Da der Winkel ist negativ, messen Sie diesen Winkel im Uhrzeigersinn.
2 Miss den Winkel Radiant. Messen Sie diesen Winkel von der Polarachse (entspricht der positiven x-Achse). Da der Winkel ist negativ, messen Sie diesen Winkel im Uhrzeigersinn. -
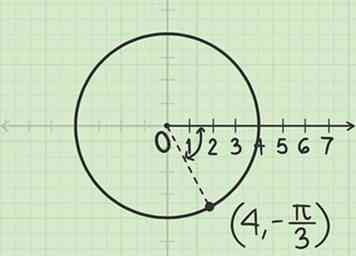 3 Zeichnen Sie eine Linie in diesem Winkel. Beginne am Pol (Ursprung). Da der Radius positiv ist, bewegen Sie sich vom Pol durch den Winkel, den Sie gemessen haben. Der Punkt, an dem die Linie den Kreis schneidet, ist .
3 Zeichnen Sie eine Linie in diesem Winkel. Beginne am Pol (Ursprung). Da der Radius positiv ist, bewegen Sie sich vom Pol durch den Winkel, den Sie gemessen haben. Der Punkt, an dem die Linie den Kreis schneidet, ist .
Zweites Beispiel
Zeichnen Sie den Punkt Q bei auf der polaren Ebene.
-
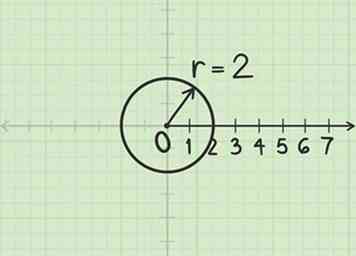 1 Konstruiere einen Kreis mit Radius . Verwenden Sie den Pfosten als Mittelpunkt. Obwohl der Radius tatsächlich -2 ist, ist das Vorzeichen für diesen Schritt nicht wichtig.
1 Konstruiere einen Kreis mit Radius . Verwenden Sie den Pfosten als Mittelpunkt. Obwohl der Radius tatsächlich -2 ist, ist das Vorzeichen für diesen Schritt nicht wichtig. -
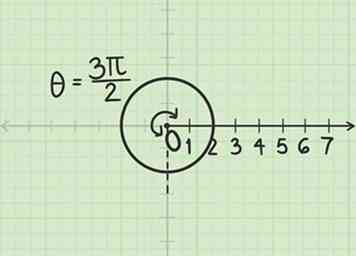 2 Miss den Winkel Radiant. Da der Winkel ist positiv, Sie müssen gegen den Uhrzeigersinn von der polaren Achse gehen.
2 Miss den Winkel Radiant. Da der Winkel ist positiv, Sie müssen gegen den Uhrzeigersinn von der polaren Achse gehen. -
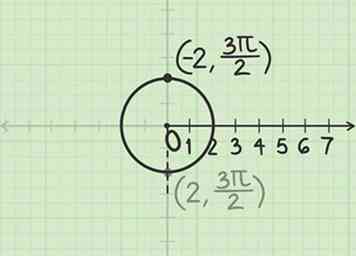 3 Konstruiere eine Linie gegenüber diesem Winkel. Seit dem Radius ist negativ, du musst vom Pol in die entgegengesetzte Richtung des gegebenen Winkels gehen. Der Punkt, an dem die Linie den Kreis schneidet, ist .
3 Konstruiere eine Linie gegenüber diesem Winkel. Seit dem Radius ist negativ, du musst vom Pol in die entgegengesetzte Richtung des gegebenen Winkels gehen. Der Punkt, an dem die Linie den Kreis schneidet, ist .
Teil vier von vier:
Konvertieren kartesischer Koordinaten in Polarkoordinaten
-
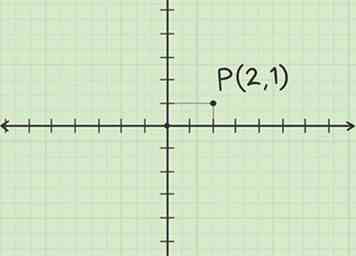 1 Betrachten Sie den Punkt in der kartesischen Ebene. Beginnen Sie am Ursprung, zeichnen Sie ein Liniensegment 2 Einheiten entlang der positiven x-Achse. Zeichnen Sie ein zweites Liniensegment von diesem Punkt 1 Einheit in das Positive y Richtung. Sie sind jetzt bei Punkt (2, 1), also beschriften Sie diesen Punkt P.
1 Betrachten Sie den Punkt in der kartesischen Ebene. Beginnen Sie am Ursprung, zeichnen Sie ein Liniensegment 2 Einheiten entlang der positiven x-Achse. Zeichnen Sie ein zweites Liniensegment von diesem Punkt 1 Einheit in das Positive y Richtung. Sie sind jetzt bei Punkt (2, 1), also beschriften Sie diesen Punkt P. -
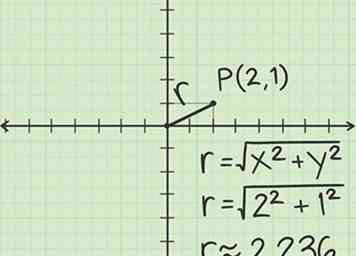 2 Finde die Entfernung zwischen dem Ursprung und . Zeichne eine Linie zwischen O und P. Diese Linie hat eine Länge in Polarkoordinaten. Es ist auch die Hypotenuse eines rechtwinkligen Dreiecks, so dass Sie die Länge der Hypotenuse mit Hilfe der Geometrie bestimmen können. Beispielsweise:
2 Finde die Entfernung zwischen dem Ursprung und . Zeichne eine Linie zwischen O und P. Diese Linie hat eine Länge in Polarkoordinaten. Es ist auch die Hypotenuse eines rechtwinkligen Dreiecks, so dass Sie die Länge der Hypotenuse mit Hilfe der Geometrie bestimmen können. Beispielsweise: - Die Beine dieses rechtwinkligen Dreiecks haben Werte von 2 und 1.
- Berechnen Sie mit dem Satz des Pythagoras, dass die Länge der Hypotenuse ist .
- Die allgemeine Formel zu finden aus kartesischen Koordinaten ist , woher ist die kartesische x-Koordinate und die kartesische Y-Koordinate.
-
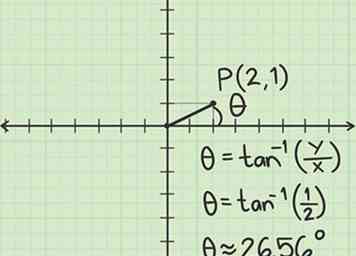 3 Finde den Winkel zwischen und die positive x-Achse. Verwenden Sie die Trigonometrie, um diesen Wert zu finden:
3 Finde den Winkel zwischen und die positive x-Achse. Verwenden Sie die Trigonometrie, um diesen Wert zu finden: -
- Die allgemeine Formel zu finden ist , woher ist die kartesische y-Koordinate und die kartesische x-Koordinate.
-
-
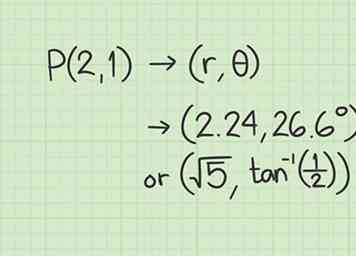 4 Schreiben Sie die Polarkoordinaten auf. Sie haben jetzt die Werte von und . Die rechtwinkligen Koordinaten (2, 1) werden in ungefähre Polarkoordinaten von (2.24, 26.6º) oder exakte Koordinaten von .
4 Schreiben Sie die Polarkoordinaten auf. Sie haben jetzt die Werte von und . Die rechtwinkligen Koordinaten (2, 1) werden in ungefähre Polarkoordinaten von (2.24, 26.6º) oder exakte Koordinaten von .
 Minotauromaquia
Minotauromaquia
 1 Richte die Polarebene ein. Sie haben wahrscheinlich zuvor Punkte mit kartesischen Koordinaten grafisch dargestellt
1 Richte die Polarebene ein. Sie haben wahrscheinlich zuvor Punkte mit kartesischen Koordinaten grafisch dargestellt  2 Verstehen Sie Polarkoordinaten. Auf der polaren Ebene wird ein Punkt durch eine Koordinate in der Form dargestellt
2 Verstehen Sie Polarkoordinaten. Auf der polaren Ebene wird ein Punkt durch eine Koordinate in der Form dargestellt 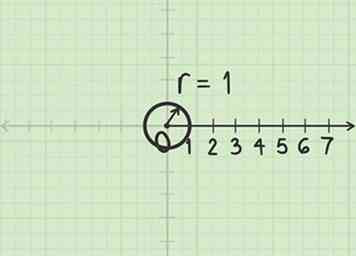 3 Überprüfen Sie den Einheitenkreis. In Polarkoordinaten wird der Winkel normalerweise im Bogenmaß anstatt in Grad gemessen. In diesem System deckt eine volle Drehung (360º oder ein voller Kreis) einen Winkel von 2 ab
3 Überprüfen Sie den Einheitenkreis. In Polarkoordinaten wird der Winkel normalerweise im Bogenmaß anstatt in Grad gemessen. In diesem System deckt eine volle Drehung (360º oder ein voller Kreis) einen Winkel von 2 ab 1 Konstruiere einen Kreis mit Radius
1 Konstruiere einen Kreis mit Radius  2 Messen Sie einen Winkel von
2 Messen Sie einen Winkel von  3 Zeichnen Sie eine Linie basierend auf dem Vorzeichen von
3 Zeichnen Sie eine Linie basierend auf dem Vorzeichen von  4 Beschriften Sie den Punkt, an dem sich die Linie und der Kreis treffen. Das ist der Punkt
4 Beschriften Sie den Punkt, an dem sich die Linie und der Kreis treffen. Das ist der Punkt  1 Konstruiere einen Kreis mit Radius
1 Konstruiere einen Kreis mit Radius  2 Miss den Winkel
2 Miss den Winkel  3 Zeichnen Sie eine Linie in diesem Winkel. Beginne am Pol (Ursprung). Da der Radius positiv ist, bewegen Sie sich vom Pol durch den Winkel, den Sie gemessen haben. Der Punkt, an dem die Linie den Kreis schneidet, ist
3 Zeichnen Sie eine Linie in diesem Winkel. Beginne am Pol (Ursprung). Da der Radius positiv ist, bewegen Sie sich vom Pol durch den Winkel, den Sie gemessen haben. Der Punkt, an dem die Linie den Kreis schneidet, ist  1 Konstruiere einen Kreis mit Radius
1 Konstruiere einen Kreis mit Radius  2 Miss den Winkel
2 Miss den Winkel  3 Konstruiere eine Linie gegenüber diesem Winkel. Seit dem Radius
3 Konstruiere eine Linie gegenüber diesem Winkel. Seit dem Radius  1 Betrachten Sie den Punkt
1 Betrachten Sie den Punkt 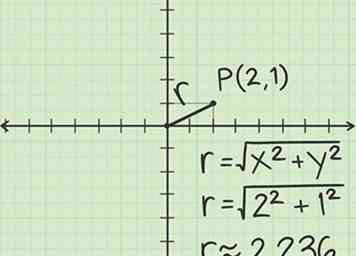 2 Finde die Entfernung zwischen dem Ursprung
2 Finde die Entfernung zwischen dem Ursprung 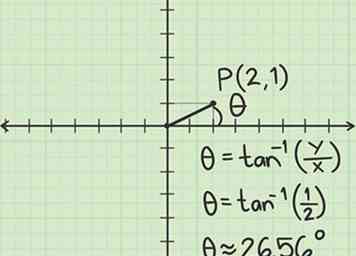 3 Finde den Winkel zwischen
3 Finde den Winkel zwischen 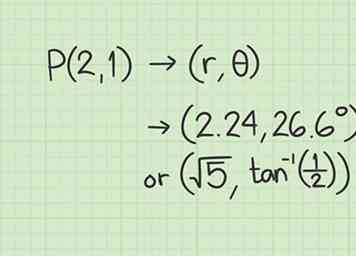 4 Schreiben Sie die Polarkoordinaten auf. Sie haben jetzt die Werte von
4 Schreiben Sie die Polarkoordinaten auf. Sie haben jetzt die Werte von