Das Mandelbrot - Set besteht aus Punkten, die auf einer komplexen Ebene aufgetragen sind, um ein Fraktal: eine auffällige Form oder Form, in der jeder Teil tatsächlich eine Miniaturkopie des Ganzen ist. Die unglaubliche schillernde Bildsprache, die im Mandelbrot-Set versteckt war, konnte man im 16. Jahrhundert dank Rafael Bombellis Verständnis von imaginären Zahlen sehen - aber erst als Benoit Mandelbrot und andere mit Hilfe von Computern Fraktale erkundeten, wurde das geheime Universum enthüllt .
Jetzt, wo wir wissen, dass es existiert, können wir es primitiver angehen: per Hand. Hier ist eine Methode, eine rohe Wiedergabe des Sets zu betrachten, nur um zu verstehen, wie es gemacht wird; Sie erhalten dann eine viel tiefere Wertschätzung für die Renderings, die Sie mit den vielen verfügbaren Open-Source-Computerprogrammen machen können, oder die Sie auf CD-ROM und DVD ansehen können.
Schritte
-
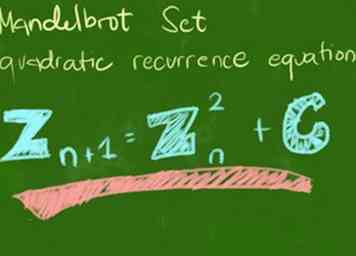 1 Verstehen Sie die Grundformel, oft ausgedrückt als z = z2 + c. Das bedeutet einfach, dass wir für jeden Punkt im Mandelbrot-Universum, den wir sehen wollen, weiterrechnen z bis eine von zwei Bedingungen auftritt; Dann färben wir es, um zu zeigen, wie viele Berechnungen wir gemacht haben. Mach dir keine Sorgen! Dies wird in den folgenden Schritten deutlich werden.
1 Verstehen Sie die Grundformel, oft ausgedrückt als z = z2 + c. Das bedeutet einfach, dass wir für jeden Punkt im Mandelbrot-Universum, den wir sehen wollen, weiterrechnen z bis eine von zwei Bedingungen auftritt; Dann färben wir es, um zu zeigen, wie viele Berechnungen wir gemacht haben. Mach dir keine Sorgen! Dies wird in den folgenden Schritten deutlich werden. -
 2 Besorge 3 verschiedene Buntstifte oder Buntstifte oder Marker mit Filzstiften und einen schwarzen Stift, um den Umriss zu erstellen. Der Grund, warum wir drei Farben wollen, ist, weil wir eine erste Annäherung mit nicht mehr als 3 Iterationen machen (Pässe, oder mit anderen Worten, die Formel bis zu 3 Mal pro Punkt anwenden):
2 Besorge 3 verschiedene Buntstifte oder Buntstifte oder Marker mit Filzstiften und einen schwarzen Stift, um den Umriss zu erstellen. Der Grund, warum wir drei Farben wollen, ist, weil wir eine erste Annäherung mit nicht mehr als 3 Iterationen machen (Pässe, oder mit anderen Worten, die Formel bis zu 3 Mal pro Punkt anwenden): -
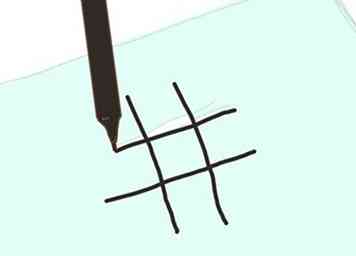 3 Zeichnen Sie mit dem schwarzen Marker ein großes Tic-Tac-Toe-Brett, 3 mal 3 Quadrate, auf ein Blatt Papier.
3 Zeichnen Sie mit dem schwarzen Marker ein großes Tic-Tac-Toe-Brett, 3 mal 3 Quadrate, auf ein Blatt Papier. -
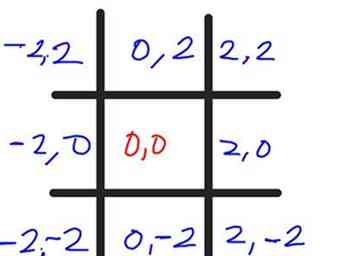 4 Etikett (auch in schwarz) das mittlere Quadrat (0, 0). Dies ist die Konstante (c) Wert des Punktes in der exakten Mitte des Quadrats. Nehmen wir an, jedes Quadrat ist 2 Einheiten breit, also addiere und / oder subtrahiere 2 von / zu x und y Werte von jedem Quadrat, mit x ist die erste Nummer und y die zweite Nummer sein. Wenn Sie fertig sind, wird es wie das aussehen, was Sie hier sehen. Immer wenn Sie den Zellen folgen, sollten die y-Werte (die zweite Zahl) gleich sein; Wenn Sie den Zellen nach unten folgen, sollten die x-Werte (die erste Zahl) gleich sein.
4 Etikett (auch in schwarz) das mittlere Quadrat (0, 0). Dies ist die Konstante (c) Wert des Punktes in der exakten Mitte des Quadrats. Nehmen wir an, jedes Quadrat ist 2 Einheiten breit, also addiere und / oder subtrahiere 2 von / zu x und y Werte von jedem Quadrat, mit x ist die erste Nummer und y die zweite Nummer sein. Wenn Sie fertig sind, wird es wie das aussehen, was Sie hier sehen. Immer wenn Sie den Zellen folgen, sollten die y-Werte (die zweite Zahl) gleich sein; Wenn Sie den Zellen nach unten folgen, sollten die x-Werte (die erste Zahl) gleich sein. - 5 Berechnen Sie den ersten Durchgang, oder Iteration, der Formel. Sie, als der Computer (eigentlich, die ursprüngliche Bedeutung des Wortes war "eine Person, die berechnet") kann dies selbst tun. Fangen wir mit diesen Annahmen an:
- Der Anfangs-z-Wert jedes Quadrats ist (0, 0). Wenn der absolute Wert von z für einen gegebenen Punkt größer oder gleich 2 ist, wird gesagt, dass dieser Punkt (und sein entsprechendes Quadrat) den Wert hat entkam das Mandelbrot-Set. Wenn das passiert, werden Sie das Quadrat entsprechend der Anzahl der Iterationen der Formel färben, die Sie auf diesen Punkt angewendet haben.
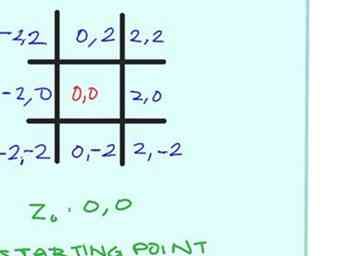
- Wählen Sie die Farben aus, die Sie für Pass 1, Pass 2 und Pass 3 verwenden. Nehmen wir für die Zwecke dieses Artikels jeweils Rot, Grün und Blau an.
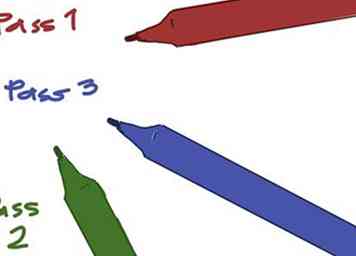
- Berechnen Sie den Wert von z für die obere linke Ecke des Tic-Tac-Toe-Boards unter Annahme eines Anfangs-Z-Werts von 0 + 0i oder (0, 0) (siehe Tipps zum besseren Verständnis dieser Darstellungen). Wir benutzen die Formel z = z2 + c wie im ersten Schritt beschrieben. Sie werden schnell sehen, dass in diesem Fall z2+ c ist einfach c, da Nullquadrat immer noch Null ist. Und was ist c für dieses Quadrat? (-2, 2).
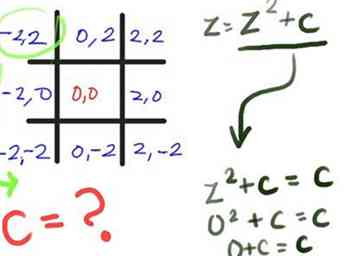
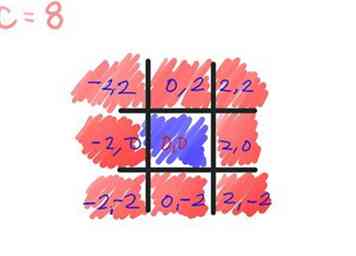
- Bestimmen Sie den absoluten Wert dieses Punktes; Der absolute Wert einer komplexen Zahl (a, b) ist die Quadratwurzel von a2 + b2. Jetzt werden wir dies mit einem bekannten Wert vergleichen: 2können wir es vermeiden, durch das Vergleichen von a2 + b2 zu 22, die wir kennen, ist gleich 4. In dieser Berechnung ist a = -2 und b = 2.

- ([-2]2 + 22) =
- (4 + 4) =
- 8, die größer als 4 ist.
- Es ist dem Mandelbrot-Set nach der ersten Berechnung entgangen, da sein absoluter Wert größer als 2 ist. Färben Sie es mit dem Bleistift, den Sie für den Durchlauf 1 gewählt haben.
-
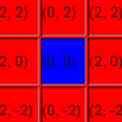 Tue dasselbe für jedes Feld auf dem Spielfeld, außer für das mittlere Quadrat, das dem Mandelbrot nicht entgeht, das durch den dritten Durchgang gesetzt wurde (noch wird es jemals entkommen). Sie haben also nur zwei Farben verwendet: die Farbe Pass 1 für alle äußeren Quadrate und die Farbe Pass 3 für das mittlere Quadrat.
Tue dasselbe für jedes Feld auf dem Spielfeld, außer für das mittlere Quadrat, das dem Mandelbrot nicht entgeht, das durch den dritten Durchgang gesetzt wurde (noch wird es jemals entkommen). Sie haben also nur zwei Farben verwendet: die Farbe Pass 1 für alle äußeren Quadrate und die Farbe Pass 3 für das mittlere Quadrat.
- Der Anfangs-z-Wert jedes Quadrats ist (0, 0). Wenn der absolute Wert von z für einen gegebenen Punkt größer oder gleich 2 ist, wird gesagt, dass dieser Punkt (und sein entsprechendes Quadrat) den Wert hat entkam das Mandelbrot-Set. Wenn das passiert, werden Sie das Quadrat entsprechend der Anzahl der Iterationen der Formel färben, die Sie auf diesen Punkt angewendet haben.
-
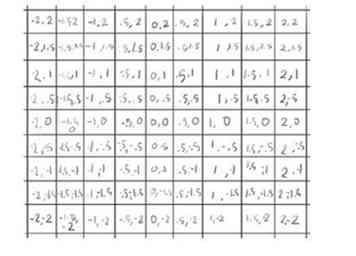 6 Versuchen wir ein Quadrat 3 mal größer, 9 von 9, aber immer noch maximal 3 Iterationen.
6 Versuchen wir ein Quadrat 3 mal größer, 9 von 9, aber immer noch maximal 3 Iterationen. - 7 Beginnen Sie mit der dritten Reihe, denn dort wird es sofort interessant.
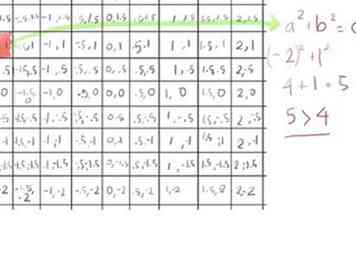
- Das erste Element (-2, 1) ist größer als 2 (weil (-2)2 + 12 stellt sich heraus, dass es 5) ist, also malen wir dieses eine rot, da es dem Mandelbrot beim ersten Durchgang entgeht.
- Das zweite Element (-1.5, 1) ist nicht größer als 2. Die Formel für den absoluten Wert wird angewendet, x2+ y2, mit x = -1,5 und y = 1:
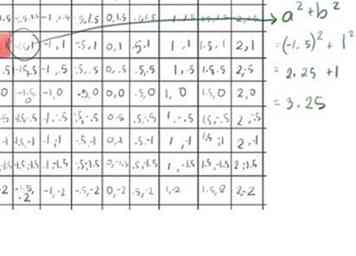
- (-1.5)2 = 2.25
- 12 = 1
- 2,25 + 1 = 3,25, weniger als 4, also ist die Quadratwurzel kleiner als 2.
- Also gehen wir zu unserem zweiten Durchlauf über und berechnen z2+ c mit der Tastenkombination (x2-y2, 2xy) für z2 (siehe Tipps, wie diese Verknüpfung abgeleitet wird), immer noch mit x = -1,5 und y = 1:
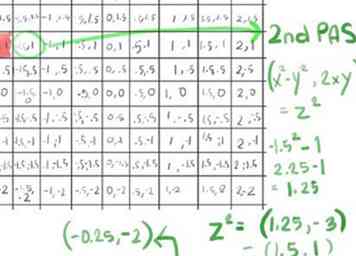
- (-1.5)2 - 12 wird 2.25 - 1, was wird 1.25;
- 2xy, da x -1,5 ist und y 1 ist, wird 2 (-1,5), was ergibt -3.0;
- Dies gibt uns eine z2 von (1,25, -3)
- Jetzt hinzufügen c für diese Zelle (füge x zu x, y zu y) hinzu (-0.25, -2)
- Lassen Sie uns testen, ob sein absoluter Wert jetzt größer als 2: ist. Berechne x2 + y2:
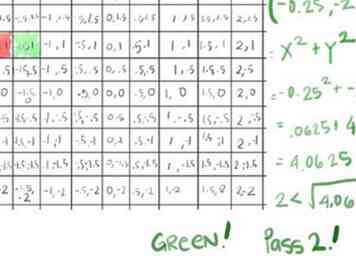
- (-.25)2 = .0625
- -22 = 4
- .0625 + 4 = 4.0625, deren Quadratwurzel größer als 2 ist, ist also nach der zweiten Iteration ausgebrochen: unser erstes Grün!
- Wenn Sie sich mit den Berechnungen vertraut gemacht haben, werden Sie manchmal in der Lage sein zu erkennen, welche dem Mandelbrot-Set entgehen, indem Sie einfach auf die Zahlen schauen.In diesem Beispiel hat die y-Komponente eine Größe von 2, die, wenn sie quadriert und zum Quadratwert der anderen Zahl addiert wird, größer als 4 ist. Jede Zahl größer als 4 hat eine Quadratwurzel größer als 2. Siehe die Tipps unten für eine detailliertere Erklärung.
- Das dritte Element mit einem c-Wert von (-1, 1) entgeht nicht dem ersten Durchgang: da sowohl 1 als auch -1 im Quadrat 1 ist, x2+ y2 ist 2. Also berechnen wir z2+ c, mit der Tastenkombination (x2-y2, 2xy) für z2:

- (-1)2-12 wird 1-1, was 0 ist;
- 2xy ist dann 2 (-1) = -2;
- z2 = (0, -2)
- addieren wir c (0, -2) + (-1, 1) = (-1, -1)
- Das ist immer noch der gleiche absolute Wert wie zuvor (die Quadratwurzel von zwei, etwa 1,41); Fortsetzung mit einer dritten Iteration:
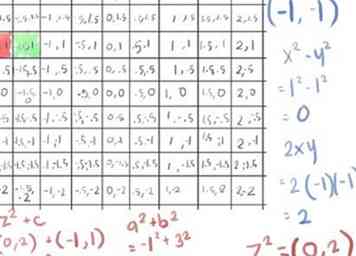
- ([-1]2)-([-1]2) wird 1-1, das ist 0 (noch einmal) ...
- aber jetzt ist 2xy 2 (-1) (-1), was positiv 2 ist, was zu einem z führt2 Wert von (0, 2)
- addieren wir c (0, 2) + (-1, 1) = (-1, 3), was ein a hat2 + b2 von 10, viel größer als 4.
- So entgeht auch dieser. Färben Sie die Zelle mit Ihrer dritten Farbe, blau, und fahren Sie mit der nächsten Farbe fort, da wir drei Iterationen mit diesem Punkt abgeschlossen haben.
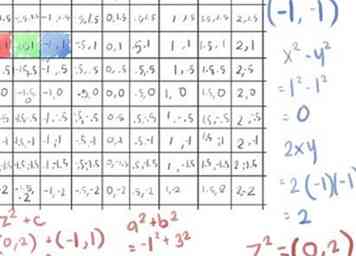
- Die Tatsache, dass wir nur drei Farben verwenden, wird hier als ein Problem sichtbar, da etwas, das nach nur drei Iterationen verschwindet, dasselbe wie (0, 0) ist noch nie entkommt; offensichtlich werden wir auf dieser Detailebene noch immer nichts in der Nähe des Mandelbrot "Bugs" sehen.
- Das erste Element (-2, 1) ist größer als 2 (weil (-2)2 + 12 stellt sich heraus, dass es 5) ist, also malen wir dieses eine rot, da es dem Mandelbrot beim ersten Durchgang entgeht.
-
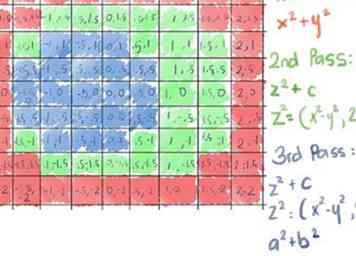 8 Fahren Sie fort, jede Zelle zu berechnen bis es ausgeblendet wurde oder die maximale Anzahl von Iterationen erreicht ist (die Anzahl der verwendeten Farben: 3 in diesem Beispiel), an dem Sie es färben. So sieht die 9 mal 9 Matrix nach 3 Wiederholungen auf jedem Quadrat aus ... Sieht aus, als wären wir auf etwas!
8 Fahren Sie fort, jede Zelle zu berechnen bis es ausgeblendet wurde oder die maximale Anzahl von Iterationen erreicht ist (die Anzahl der verwendeten Farben: 3 in diesem Beispiel), an dem Sie es färben. So sieht die 9 mal 9 Matrix nach 3 Wiederholungen auf jedem Quadrat aus ... Sieht aus, als wären wir auf etwas! - 9 Wiederhole die gleiche Matrix erneut mit mehr Farben (Iterationen), um die nächsten Schichten aufzudecken, oder besser, zeichne eine viel größere Matrix für ein längerfristiges Projekt auf! Sie erhalten genauere Bilder von:
-
 Erhöhen der Anzahl der Zellen; Dies hat 81 Zellen pro Seite. Beachten Sie die Ähnlichkeit mit der obigen 9 mal 9 Matrix, aber die viel glatteren Kanten auf dem Kreis und Oval.
Erhöhen der Anzahl der Zellen; Dies hat 81 Zellen pro Seite. Beachten Sie die Ähnlichkeit mit der obigen 9 mal 9 Matrix, aber die viel glatteren Kanten auf dem Kreis und Oval. -
 Erhöhen der Anzahl der Farben (Iterationen); Dies hat 256 Farben von rot, grün und blau für insgesamt 768 Farben im Vergleich zu 3. Beachten Sie, dass Sie jetzt die Umrisse des bekannten Mandelbrot "See" (oder "Bug", je nachdem, wie Sie aussehen) sehen können daran). Der Nachteil ist die Zeit, die es braucht; Wenn Sie jede Iteration in 10 Sekunden berechnen können, sind das ungefähr 2 Stunden für jede Zelle in oder in der Nähe des Mandelbrot-Sees. Obwohl das ein relativ kleiner Teil der Matrix 81 zu 81 ist, würde es wahrscheinlich noch ein Jahr dauern, um es zu vervollständigen, selbst wenn Sie jeden Tag mehrere Stunden daran gearbeitet haben. Hier kommt der Silizium-Computer zum Einsatz.
Erhöhen der Anzahl der Farben (Iterationen); Dies hat 256 Farben von rot, grün und blau für insgesamt 768 Farben im Vergleich zu 3. Beachten Sie, dass Sie jetzt die Umrisse des bekannten Mandelbrot "See" (oder "Bug", je nachdem, wie Sie aussehen) sehen können daran). Der Nachteil ist die Zeit, die es braucht; Wenn Sie jede Iteration in 10 Sekunden berechnen können, sind das ungefähr 2 Stunden für jede Zelle in oder in der Nähe des Mandelbrot-Sees. Obwohl das ein relativ kleiner Teil der Matrix 81 zu 81 ist, würde es wahrscheinlich noch ein Jahr dauern, um es zu vervollständigen, selbst wenn Sie jeden Tag mehrere Stunden daran gearbeitet haben. Hier kommt der Silizium-Computer zum Einsatz.
-
 Minotauromaquia
Minotauromaquia
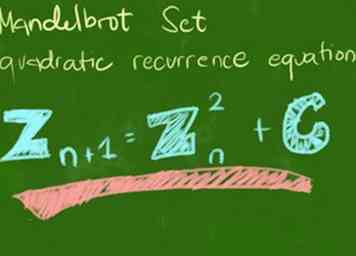 1 Verstehen Sie die Grundformel, oft ausgedrückt als z = z2 + c. Das bedeutet einfach, dass wir für jeden Punkt im Mandelbrot-Universum, den wir sehen wollen, weiterrechnen z bis eine von zwei Bedingungen auftritt; Dann färben wir es, um zu zeigen, wie viele Berechnungen wir gemacht haben. Mach dir keine Sorgen! Dies wird in den folgenden Schritten deutlich werden.
1 Verstehen Sie die Grundformel, oft ausgedrückt als z = z2 + c. Das bedeutet einfach, dass wir für jeden Punkt im Mandelbrot-Universum, den wir sehen wollen, weiterrechnen z bis eine von zwei Bedingungen auftritt; Dann färben wir es, um zu zeigen, wie viele Berechnungen wir gemacht haben. Mach dir keine Sorgen! Dies wird in den folgenden Schritten deutlich werden.  2 Besorge 3 verschiedene Buntstifte oder Buntstifte oder Marker mit Filzstiften und einen schwarzen Stift, um den Umriss zu erstellen. Der Grund, warum wir drei Farben wollen, ist, weil wir eine erste Annäherung mit nicht mehr als 3 Iterationen machen (Pässe, oder mit anderen Worten, die Formel bis zu 3 Mal pro Punkt anwenden):
2 Besorge 3 verschiedene Buntstifte oder Buntstifte oder Marker mit Filzstiften und einen schwarzen Stift, um den Umriss zu erstellen. Der Grund, warum wir drei Farben wollen, ist, weil wir eine erste Annäherung mit nicht mehr als 3 Iterationen machen (Pässe, oder mit anderen Worten, die Formel bis zu 3 Mal pro Punkt anwenden):  3 Zeichnen Sie mit dem schwarzen Marker ein großes Tic-Tac-Toe-Brett, 3 mal 3 Quadrate, auf ein Blatt Papier.
3 Zeichnen Sie mit dem schwarzen Marker ein großes Tic-Tac-Toe-Brett, 3 mal 3 Quadrate, auf ein Blatt Papier.  4 Etikett (auch in schwarz) das mittlere Quadrat (0, 0). Dies ist die Konstante (c) Wert des Punktes in der exakten Mitte des Quadrats. Nehmen wir an, jedes Quadrat ist 2 Einheiten breit, also addiere und / oder subtrahiere 2 von / zu x und y Werte von jedem Quadrat, mit x ist die erste Nummer und y die zweite Nummer sein. Wenn Sie fertig sind, wird es wie das aussehen, was Sie hier sehen. Immer wenn Sie den Zellen folgen, sollten die y-Werte (die zweite Zahl) gleich sein; Wenn Sie den Zellen nach unten folgen, sollten die x-Werte (die erste Zahl) gleich sein.
4 Etikett (auch in schwarz) das mittlere Quadrat (0, 0). Dies ist die Konstante (c) Wert des Punktes in der exakten Mitte des Quadrats. Nehmen wir an, jedes Quadrat ist 2 Einheiten breit, also addiere und / oder subtrahiere 2 von / zu x und y Werte von jedem Quadrat, mit x ist die erste Nummer und y die zweite Nummer sein. Wenn Sie fertig sind, wird es wie das aussehen, was Sie hier sehen. Immer wenn Sie den Zellen folgen, sollten die y-Werte (die zweite Zahl) gleich sein; Wenn Sie den Zellen nach unten folgen, sollten die x-Werte (die erste Zahl) gleich sein. 

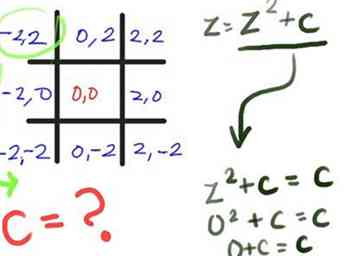


 Tue dasselbe für jedes Feld auf dem Spielfeld, außer für das mittlere Quadrat, das dem Mandelbrot nicht entgeht, das durch den dritten Durchgang gesetzt wurde (noch wird es jemals entkommen). Sie haben also nur zwei Farben verwendet: die Farbe Pass 1 für alle äußeren Quadrate und die Farbe Pass 3 für das mittlere Quadrat.
Tue dasselbe für jedes Feld auf dem Spielfeld, außer für das mittlere Quadrat, das dem Mandelbrot nicht entgeht, das durch den dritten Durchgang gesetzt wurde (noch wird es jemals entkommen). Sie haben also nur zwei Farben verwendet: die Farbe Pass 1 für alle äußeren Quadrate und die Farbe Pass 3 für das mittlere Quadrat. 6 Versuchen wir ein Quadrat 3 mal größer, 9 von 9, aber immer noch maximal 3 Iterationen.
6 Versuchen wir ein Quadrat 3 mal größer, 9 von 9, aber immer noch maximal 3 Iterationen. 






 8 Fahren Sie fort, jede Zelle zu berechnen bis es ausgeblendet wurde oder die maximale Anzahl von Iterationen erreicht ist (die Anzahl der verwendeten Farben: 3 in diesem Beispiel), an dem Sie es färben. So sieht die 9 mal 9 Matrix nach 3 Wiederholungen auf jedem Quadrat aus ... Sieht aus, als wären wir auf etwas!
8 Fahren Sie fort, jede Zelle zu berechnen bis es ausgeblendet wurde oder die maximale Anzahl von Iterationen erreicht ist (die Anzahl der verwendeten Farben: 3 in diesem Beispiel), an dem Sie es färben. So sieht die 9 mal 9 Matrix nach 3 Wiederholungen auf jedem Quadrat aus ... Sieht aus, als wären wir auf etwas!  Erhöhen der Anzahl der Zellen; Dies hat 81 Zellen pro Seite. Beachten Sie die Ähnlichkeit mit der obigen 9 mal 9 Matrix, aber die viel glatteren Kanten auf dem Kreis und Oval.
Erhöhen der Anzahl der Zellen; Dies hat 81 Zellen pro Seite. Beachten Sie die Ähnlichkeit mit der obigen 9 mal 9 Matrix, aber die viel glatteren Kanten auf dem Kreis und Oval. Erhöhen der Anzahl der Farben (Iterationen); Dies hat 256 Farben von rot, grün und blau für insgesamt 768 Farben im Vergleich zu 3. Beachten Sie, dass Sie jetzt die Umrisse des bekannten Mandelbrot "See" (oder "Bug", je nachdem, wie Sie aussehen) sehen können daran). Der Nachteil ist die Zeit, die es braucht; Wenn Sie jede Iteration in 10 Sekunden berechnen können, sind das ungefähr 2 Stunden für jede Zelle in oder in der Nähe des Mandelbrot-Sees. Obwohl das ein relativ kleiner Teil der Matrix 81 zu 81 ist, würde es wahrscheinlich noch ein Jahr dauern, um es zu vervollständigen, selbst wenn Sie jeden Tag mehrere Stunden daran gearbeitet haben. Hier kommt der Silizium-Computer zum Einsatz.
Erhöhen der Anzahl der Farben (Iterationen); Dies hat 256 Farben von rot, grün und blau für insgesamt 768 Farben im Vergleich zu 3. Beachten Sie, dass Sie jetzt die Umrisse des bekannten Mandelbrot "See" (oder "Bug", je nachdem, wie Sie aussehen) sehen können daran). Der Nachteil ist die Zeit, die es braucht; Wenn Sie jede Iteration in 10 Sekunden berechnen können, sind das ungefähr 2 Stunden für jede Zelle in oder in der Nähe des Mandelbrot-Sees. Obwohl das ein relativ kleiner Teil der Matrix 81 zu 81 ist, würde es wahrscheinlich noch ein Jahr dauern, um es zu vervollständigen, selbst wenn Sie jeden Tag mehrere Stunden daran gearbeitet haben. Hier kommt der Silizium-Computer zum Einsatz.