Um die Fläche eines Dreiecks zu berechnen, müssen Sie dessen Höhe kennen. Um die Höhe zu finden, folgen Sie diesen Anweisungen. Sie müssen mindestens eine Basis haben, um die Höhe zu finden.
Methode eins von dreien:
Verwenden von Base und Area zum Suchen der Höhe
-
 1 Erinnern Sie sich an die Formel für die Fläche eines Dreiecks. Die Formel für die Fläche eines Dreiecks ist A = 1 / 2bh. [1]
1 Erinnern Sie sich an die Formel für die Fläche eines Dreiecks. Die Formel für die Fläche eines Dreiecks ist A = 1 / 2bh. [1] - EIN = Fläche des Dreiecks
- b = Länge der Basis des Dreiecks
- h = Höhe der Basis des Dreiecks
-
 2 Schau dir dein Dreieck an und ermittle, welche Variablen du kennst. Sie kennen den Bereich bereits, weisen Sie diesen Wert also zu EIN. Sie sollten auch den Wert einer Seitenlänge kennen; Weisen Sie diesen Wert "b" zu. Jede Seite eines Dreiecks kann die Basis sein, unabhängig davon, wie das Dreieck gezeichnet wird. Um dies zu visualisieren, stellen Sie sich vor, das Dreieck zu drehen, bis die bekannte Seitenlänge unten ist. Beispiel
2 Schau dir dein Dreieck an und ermittle, welche Variablen du kennst. Sie kennen den Bereich bereits, weisen Sie diesen Wert also zu EIN. Sie sollten auch den Wert einer Seitenlänge kennen; Weisen Sie diesen Wert "b" zu. Jede Seite eines Dreiecks kann die Basis sein, unabhängig davon, wie das Dreieck gezeichnet wird. Um dies zu visualisieren, stellen Sie sich vor, das Dreieck zu drehen, bis die bekannte Seitenlänge unten ist. Beispiel
Wenn Sie wissen, dass die Fläche eines Dreiecks 20 ist und eine Seite 4 ist, dann:
A = 20 und b = 4.
-
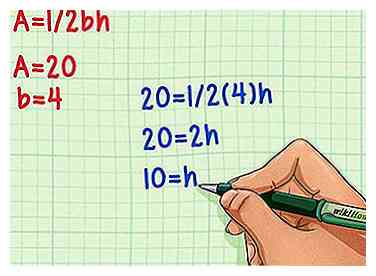 3 Schließen Sie Ihre Werte in die Gleichung ein A = 1 / 2bh und mach die Mathematik. Multiplizieren Sie zuerst die Basis (b) mit 1/2 und teilen Sie dann die Fläche (A) mit dem Produkt. Der resultierende Wert entspricht der Höhe Ihres Dreiecks! Beispiel
3 Schließen Sie Ihre Werte in die Gleichung ein A = 1 / 2bh und mach die Mathematik. Multiplizieren Sie zuerst die Basis (b) mit 1/2 und teilen Sie dann die Fläche (A) mit dem Produkt. Der resultierende Wert entspricht der Höhe Ihres Dreiecks! Beispiel
20 = 1/2 (4) h Stecke die Zahlen in die Gleichung.
20 = 2h Multiplizieren Sie 4 mit 1/2.
10 = h Teilen Sie mit 2, um den Wert für die Höhe zu finden.
Methode zwei von drei:
Die Höhe eines gleichseitigen Dreiecks finden
-
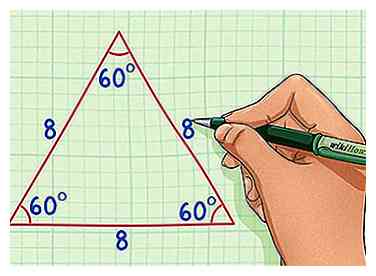 1 Erinnern Sie sich an die Eigenschaften eines gleichseitigen Dreiecks. Ein gleichseitiges Dreieck hat drei gleiche Seiten und drei gleiche Winkel, die jeweils 60 Grad betragen. Wenn Sie ein gleichseitiges Dreieck halbieren, erhalten Sie zwei kongruente rechtwinklige Dreiecke. [2]
1 Erinnern Sie sich an die Eigenschaften eines gleichseitigen Dreiecks. Ein gleichseitiges Dreieck hat drei gleiche Seiten und drei gleiche Winkel, die jeweils 60 Grad betragen. Wenn Sie ein gleichseitiges Dreieck halbieren, erhalten Sie zwei kongruente rechtwinklige Dreiecke. [2] - In diesem Beispiel verwenden wir ein gleichseitiges Dreieck mit Seitenlängen von 8.
-
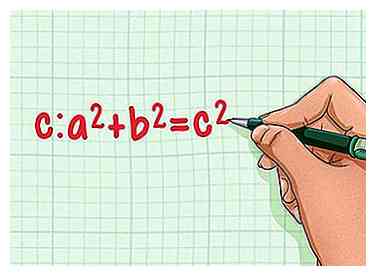 2 Erinnern Sie sich an den Satz des Pythagoras. Der Satz des Pythagoras besagt, dass für jedes rechte Dreieck mit Seitenlängen ein und bund Hypotenuse der Länge c: ein2 + b2 = c2. Wir können diesen Satz benutzen, um die Höhe unseres gleichseitigen Dreiecks zu finden![3]
2 Erinnern Sie sich an den Satz des Pythagoras. Der Satz des Pythagoras besagt, dass für jedes rechte Dreieck mit Seitenlängen ein und bund Hypotenuse der Länge c: ein2 + b2 = c2. Wir können diesen Satz benutzen, um die Höhe unseres gleichseitigen Dreiecks zu finden![3] -
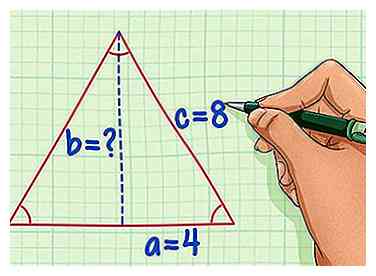 3 Brechen Sie das gleichseitige Dreieck in zwei Hälften und weisen Sie Variablen Werte zu ein, b, und c. Die Hypotenuse c wird gleich der ursprünglichen Seitenlänge sein. Seite ein wird gleich der halben Seitenlänge und Seite sein b ist die Höhe des Dreiecks, das wir lösen müssen.
3 Brechen Sie das gleichseitige Dreieck in zwei Hälften und weisen Sie Variablen Werte zu ein, b, und c. Die Hypotenuse c wird gleich der ursprünglichen Seitenlänge sein. Seite ein wird gleich der halben Seitenlänge und Seite sein b ist die Höhe des Dreiecks, das wir lösen müssen. - Mit unserem Beispiel ein gleichseitiges Dreieck mit Seiten von 8, c = 8 und a = 4.
-
 4 Stecke die Werte in den Satz des Pythagoras und löse nach b2. Erstes Quadrat c und ein indem Sie jede Zahl einzeln multiplizieren. Dann a subtrahieren2 von c2. Beispiel
4 Stecke die Werte in den Satz des Pythagoras und löse nach b2. Erstes Quadrat c und ein indem Sie jede Zahl einzeln multiplizieren. Dann a subtrahieren2 von c2. Beispiel
42 + b2 = 82 Fügen Sie die Werte für a und c ein.
16 + b2 = 64 Platz a und c.
b2 = 48 Subtrahieren a2 von c2.
-
 5 Finde die Quadratwurzel von b2 um die Höhe deines Dreiecks zu erhalten! Verwenden Sie die Quadratwurzelfunktion auf Ihrem Taschenrechner, um Sqrt (2. Die Antwort ist die Höhe deines gleichseitigen Dreiecks!
5 Finde die Quadratwurzel von b2 um die Höhe deines Dreiecks zu erhalten! Verwenden Sie die Quadratwurzelfunktion auf Ihrem Taschenrechner, um Sqrt (2. Die Antwort ist die Höhe deines gleichseitigen Dreiecks! - b = Sqrt (48) = 6.93
Methode drei von drei:
Höhe mit Winkeln und Seiten bestimmen
-
 1 Bestimmen Sie, welche Variablen Sie kennen. Die Höhe eines Dreiecks kann gefunden werden, wenn Sie zwei Seiten und den Winkel zwischen ihnen oder alle drei Seiten haben. Wir nennen die Seiten des Dreiecks a, b und c und die Winkel A, B und C.
1 Bestimmen Sie, welche Variablen Sie kennen. Die Höhe eines Dreiecks kann gefunden werden, wenn Sie zwei Seiten und den Winkel zwischen ihnen oder alle drei Seiten haben. Wir nennen die Seiten des Dreiecks a, b und c und die Winkel A, B und C. - Wenn Sie alle drei Seiten haben, verwenden Sie die Formel von Heron und die Formel für die Fläche eines Dreiecks.
- Wenn Sie zwei Seiten und einen Winkel haben, verwenden Sie die Formel für den Bereich, der aus zwei Winkeln und einer Seite besteht. A = 1 / 2ab (sin C).[4]
-
 2 Verwenden Sie Herons Formel, wenn Sie alle drei Seiten haben. Herons Formel besteht aus zwei Teilen. Zuerst müssen Sie die Variable s finden, die gleich der Hälfte des Umfangs des Dreiecks ist. Dies geschieht mit dieser Formel: s = (a + b + c) / 2.[5] Herons Formel Beispiel
2 Verwenden Sie Herons Formel, wenn Sie alle drei Seiten haben. Herons Formel besteht aus zwei Teilen. Zuerst müssen Sie die Variable s finden, die gleich der Hälfte des Umfangs des Dreiecks ist. Dies geschieht mit dieser Formel: s = (a + b + c) / 2.[5] Herons Formel Beispiel
Für ein Dreieck mit Seiten a = 4, b = 3 und c = 5:
s = (4 + 3 + 5) / 2
s = (12) / 2
s = 6
Dann benutze den zweiten Teil von Herons Formel, Bereich = sqr (s (s-a)) (s-b) (s-c). Ersetzen Sie Area in der Gleichung durch ihr Äquivalent in der Gebietsformel: 1 / 2bh (oder 1 / 2ah oder 1 / 2ch).
Löse für h. Für unser Beispieldreieck sieht das so aus:
1/2 (3) h = sqr (6 (6-4) (6-3) (6-5).
3 / 2h = sqr (6 (2) (3) (1)
3 / 2h = sqr (36)
Verwenden Sie einen Taschenrechner, um die Quadratwurzel zu berechnen, die in diesem Fall es macht 3 / 2h = 6.
Daher ist Höhe gleich 4unter Verwendung der Seite b als Basis.
-
 3 Verwenden Sie die Fläche auf zwei Seiten und eine Winkelformel, wenn Sie eine Seite und einen Winkel haben. Ersetzen Sie den Bereich in der Formel durch das Äquivalent im Bereich einer Dreiecksformel: 1 / 2bh. Dies gibt Ihnen eine Formel, die aussieht wie 1 / 2bh = 1 / 2ab (sin C). Dies kann vereinfacht werden zu h = a (sin C), wodurch eine der Seitenvariablen eliminiert wird.[6] Höhe mit 1 Seite und 1 Winkel Beispiel ermitteln
3 Verwenden Sie die Fläche auf zwei Seiten und eine Winkelformel, wenn Sie eine Seite und einen Winkel haben. Ersetzen Sie den Bereich in der Formel durch das Äquivalent im Bereich einer Dreiecksformel: 1 / 2bh. Dies gibt Ihnen eine Formel, die aussieht wie 1 / 2bh = 1 / 2ab (sin C). Dies kann vereinfacht werden zu h = a (sin C), wodurch eine der Seitenvariablen eliminiert wird.[6] Höhe mit 1 Seite und 1 Winkel Beispiel ermitteln
Zum Beispiel, mit a = 3 und C = 40 Grad, sieht die Gleichung so aus:
h = 3 (sin 40)
Verwenden Sie Ihren Rechner, um die Gleichung zu beenden, was h ungefähr 1,928 ergibt.
 Minotauromaquia
Minotauromaquia
 1 Erinnern Sie sich an die Formel für die Fläche eines Dreiecks. Die Formel für die Fläche eines Dreiecks ist A = 1 / 2bh. [1]
1 Erinnern Sie sich an die Formel für die Fläche eines Dreiecks. Die Formel für die Fläche eines Dreiecks ist A = 1 / 2bh. [1]  2 Schau dir dein Dreieck an und ermittle, welche Variablen du kennst. Sie kennen den Bereich bereits, weisen Sie diesen Wert also zu EIN. Sie sollten auch den Wert einer Seitenlänge kennen; Weisen Sie diesen Wert "b" zu. Jede Seite eines Dreiecks kann die Basis sein, unabhängig davon, wie das Dreieck gezeichnet wird. Um dies zu visualisieren, stellen Sie sich vor, das Dreieck zu drehen, bis die bekannte Seitenlänge unten ist.
2 Schau dir dein Dreieck an und ermittle, welche Variablen du kennst. Sie kennen den Bereich bereits, weisen Sie diesen Wert also zu EIN. Sie sollten auch den Wert einer Seitenlänge kennen; Weisen Sie diesen Wert "b" zu. Jede Seite eines Dreiecks kann die Basis sein, unabhängig davon, wie das Dreieck gezeichnet wird. Um dies zu visualisieren, stellen Sie sich vor, das Dreieck zu drehen, bis die bekannte Seitenlänge unten ist. 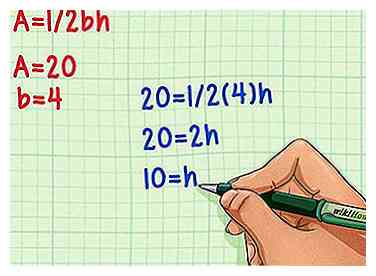 3 Schließen Sie Ihre Werte in die Gleichung ein A = 1 / 2bh und mach die Mathematik. Multiplizieren Sie zuerst die Basis (b) mit 1/2 und teilen Sie dann die Fläche (A) mit dem Produkt. Der resultierende Wert entspricht der Höhe Ihres Dreiecks!
3 Schließen Sie Ihre Werte in die Gleichung ein A = 1 / 2bh und mach die Mathematik. Multiplizieren Sie zuerst die Basis (b) mit 1/2 und teilen Sie dann die Fläche (A) mit dem Produkt. Der resultierende Wert entspricht der Höhe Ihres Dreiecks!  1 Erinnern Sie sich an die Eigenschaften eines gleichseitigen Dreiecks. Ein gleichseitiges Dreieck hat drei gleiche Seiten und drei gleiche Winkel, die jeweils 60 Grad betragen. Wenn Sie ein gleichseitiges Dreieck halbieren, erhalten Sie zwei kongruente rechtwinklige Dreiecke. [2]
1 Erinnern Sie sich an die Eigenschaften eines gleichseitigen Dreiecks. Ein gleichseitiges Dreieck hat drei gleiche Seiten und drei gleiche Winkel, die jeweils 60 Grad betragen. Wenn Sie ein gleichseitiges Dreieck halbieren, erhalten Sie zwei kongruente rechtwinklige Dreiecke. [2] 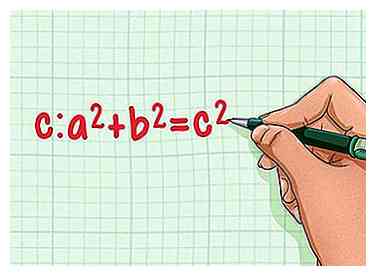 2 Erinnern Sie sich an den Satz des Pythagoras. Der Satz des Pythagoras besagt, dass für jedes rechte Dreieck mit Seitenlängen ein und bund Hypotenuse der Länge c: ein2 + b2 = c2. Wir können diesen Satz benutzen, um die Höhe unseres gleichseitigen Dreiecks zu finden![3]
2 Erinnern Sie sich an den Satz des Pythagoras. Der Satz des Pythagoras besagt, dass für jedes rechte Dreieck mit Seitenlängen ein und bund Hypotenuse der Länge c: ein2 + b2 = c2. Wir können diesen Satz benutzen, um die Höhe unseres gleichseitigen Dreiecks zu finden![3]  3 Brechen Sie das gleichseitige Dreieck in zwei Hälften und weisen Sie Variablen Werte zu ein, b, und c. Die Hypotenuse c wird gleich der ursprünglichen Seitenlänge sein. Seite ein wird gleich der halben Seitenlänge und Seite sein b ist die Höhe des Dreiecks, das wir lösen müssen.
3 Brechen Sie das gleichseitige Dreieck in zwei Hälften und weisen Sie Variablen Werte zu ein, b, und c. Die Hypotenuse c wird gleich der ursprünglichen Seitenlänge sein. Seite ein wird gleich der halben Seitenlänge und Seite sein b ist die Höhe des Dreiecks, das wir lösen müssen.  4 Stecke die Werte in den Satz des Pythagoras und löse nach b2. Erstes Quadrat c und ein indem Sie jede Zahl einzeln multiplizieren. Dann a subtrahieren2 von c2.
4 Stecke die Werte in den Satz des Pythagoras und löse nach b2. Erstes Quadrat c und ein indem Sie jede Zahl einzeln multiplizieren. Dann a subtrahieren2 von c2.  5 Finde die Quadratwurzel von b2 um die Höhe deines Dreiecks zu erhalten! Verwenden Sie die Quadratwurzelfunktion auf Ihrem Taschenrechner, um Sqrt (2. Die Antwort ist die Höhe deines gleichseitigen Dreiecks!
5 Finde die Quadratwurzel von b2 um die Höhe deines Dreiecks zu erhalten! Verwenden Sie die Quadratwurzelfunktion auf Ihrem Taschenrechner, um Sqrt (2. Die Antwort ist die Höhe deines gleichseitigen Dreiecks!  1 Bestimmen Sie, welche Variablen Sie kennen. Die Höhe eines Dreiecks kann gefunden werden, wenn Sie zwei Seiten und den Winkel zwischen ihnen oder alle drei Seiten haben. Wir nennen die Seiten des Dreiecks a, b und c und die Winkel A, B und C.
1 Bestimmen Sie, welche Variablen Sie kennen. Die Höhe eines Dreiecks kann gefunden werden, wenn Sie zwei Seiten und den Winkel zwischen ihnen oder alle drei Seiten haben. Wir nennen die Seiten des Dreiecks a, b und c und die Winkel A, B und C.  2 Verwenden Sie Herons Formel, wenn Sie alle drei Seiten haben. Herons Formel besteht aus zwei Teilen. Zuerst müssen Sie die Variable s finden, die gleich der Hälfte des Umfangs des Dreiecks ist. Dies geschieht mit dieser Formel: s = (a + b + c) / 2.[5]
2 Verwenden Sie Herons Formel, wenn Sie alle drei Seiten haben. Herons Formel besteht aus zwei Teilen. Zuerst müssen Sie die Variable s finden, die gleich der Hälfte des Umfangs des Dreiecks ist. Dies geschieht mit dieser Formel: s = (a + b + c) / 2.[5]  3 Verwenden Sie die Fläche auf zwei Seiten und eine Winkelformel, wenn Sie eine Seite und einen Winkel haben. Ersetzen Sie den Bereich in der Formel durch das Äquivalent im Bereich einer Dreiecksformel: 1 / 2bh. Dies gibt Ihnen eine Formel, die aussieht wie 1 / 2bh = 1 / 2ab (sin C). Dies kann vereinfacht werden zu h = a (sin C), wodurch eine der Seitenvariablen eliminiert wird.[6]
3 Verwenden Sie die Fläche auf zwei Seiten und eine Winkelformel, wenn Sie eine Seite und einen Winkel haben. Ersetzen Sie den Bereich in der Formel durch das Äquivalent im Bereich einer Dreiecksformel: 1 / 2bh. Dies gibt Ihnen eine Formel, die aussieht wie 1 / 2bh = 1 / 2ab (sin C). Dies kann vereinfacht werden zu h = a (sin C), wodurch eine der Seitenvariablen eliminiert wird.[6]