In der Geometrie bezieht sich der Begriff "Umfang" normalerweise auf die Gesamtabstand um die Außenseite eines Polygons, eine 2-dimensionale Form von 3 oder mehr Seiten und Winkeln. Mit anderen Worten, der Umfang einer gegebenen Form ist die Summe der Längen aller ihrer Seiten. Die Leichtigkeit, mit der der Umfang einer Form gefunden werden kann, hängt von mehreren Faktoren ab - nämlich davon, ob das Polygon a ist regulär Polygon (ein Polygon, dessen Seiten und Winkel alle gleich sind), und falls nicht, ob alle Seitenlängen in der Form bekannt sind. Wenn keine dieser Bedingungen zutrifft, hängt die Schwierigkeit, den Umfang der Form zu finden, davon ab, wie viele Informationen über die Form bekannt sind.
Schritte
-
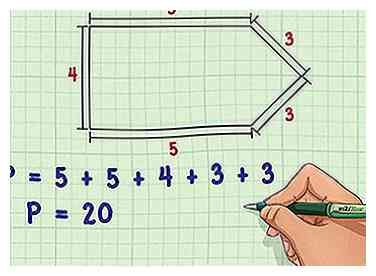 1 Suchen und addieren Sie die Längen aller Seiten des Polygons. Der Umfang von irgendein Das Polygon kann berechnet werden, indem man die Länge jeder Seite einzeln ermittelt und dann alle diese Längen addiert. Dies ist der einfachste Weg, den Umfang eines Polygons zu finden, und in Formen, in denen keine zwei Seiten gleich sind, ist dies normalerweise der einzig richtige Weg.
1 Suchen und addieren Sie die Längen aller Seiten des Polygons. Der Umfang von irgendein Das Polygon kann berechnet werden, indem man die Länge jeder Seite einzeln ermittelt und dann alle diese Längen addiert. Dies ist der einfachste Weg, den Umfang eines Polygons zu finden, und in Formen, in denen keine zwei Seiten gleich sind, ist dies normalerweise der einzig richtige Weg. - Als einfaches Beispiel hätte ein unregelmäßiges Polygon mit den Seitenlängen 5, 5, 4, 3 und 3 einen Umfang von 5 + 5 + 4 + 3 + 3 = 20
- Wenn eine oder mehrere Seitenlängen in Ihrem Polygon unbekannt sind, kann der Prozess zur Berechnung des Umfangs schwierig werden und möglicherweise komplexere Kenntnisse der Geometrie erfordern. Wenn Ihr Polygon beispielsweise ein rechtwinkliges Dreieck ist (oder in rechte Dreiecke unterteilt werden kann), kann Trigonometrie ein nützliches Werkzeug sein, um unbekannte Seiten zu finden, die verhindern, dass Sie den Umfang der Form selbst finden.
-
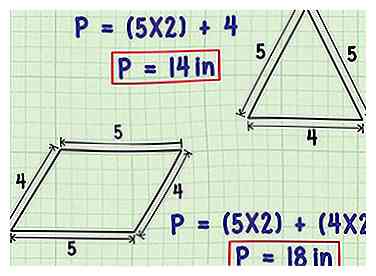 2 Multiplizieren Sie die Längen gleicher Seiten mit der Anzahl gleicher Seiten. Bestimmte Arten von Polygonen haben zwei oder mehr gleiche Seiten. Zum Beispiel haben gleichschenklige Dreiecke und gleichschenklige Trapeze 2 der Seiten mit der gleichen Länge, während Parallelogramme und Rechtecke 2 Paare gegenüberliegender Seiten mit gleicher Länge aufweisen. In diesen Fällen können Sie, wenn Sie die Länge einer der identischen Seiten kennen, diese Länge mit der Anzahl der Seiten multiplizieren, die diese Länge teilen, und dann die Längen aller ungleichen Seiten addieren, um den Umfang der Gesamtform zu finden.
2 Multiplizieren Sie die Längen gleicher Seiten mit der Anzahl gleicher Seiten. Bestimmte Arten von Polygonen haben zwei oder mehr gleiche Seiten. Zum Beispiel haben gleichschenklige Dreiecke und gleichschenklige Trapeze 2 der Seiten mit der gleichen Länge, während Parallelogramme und Rechtecke 2 Paare gegenüberliegender Seiten mit gleicher Länge aufweisen. In diesen Fällen können Sie, wenn Sie die Länge einer der identischen Seiten kennen, diese Länge mit der Anzahl der Seiten multiplizieren, die diese Länge teilen, und dann die Längen aller ungleichen Seiten addieren, um den Umfang der Gesamtform zu finden. - Betrachten wir zum Beispiel ein gleichschenkliges Dreieck, das zwei Seiten mit einer Länge von 5 Zoll (12,7 cm) und eine Seite mit einer Länge von 4 Zoll (10,2 cm) aufweist. Um den Umfang zu finden, würden wir hier die Länge der gleichen Seiten (5) nehmen und sie mit der Anzahl der gleichen Seiten (2) multiplizieren, dann die Längen der verbleibenden ungleichen Seite addieren. (5 × 2) + 4 = 10 + 4 = 14 Zoll (35,6 cm).
- Als ein Beispiel für eine Form mit mehreren Paaren gleicher Seiten betrachten wir ein Parallelogramm mit zwei Seiten mit einer Länge von 5 Zoll (12,7 cm) und zwei mit einer Länge von 4. Um den Umfang zu finden, multiplizieren wir die Länge der längere Seite um 2 und die Länge der kürzeren Seite um, dann fügen Sie die Produkte zusammen. (2 × 5) + (2 × 4) = 10 + 8 = 18 Zoll (45,7 cm).
- Beachten Sie, dass diese Methode auch für Quadrate und Rauten verwendet werden kann, die zusammen mit Rechtecken Sonderfälle von Parallelogrammen sind.
-
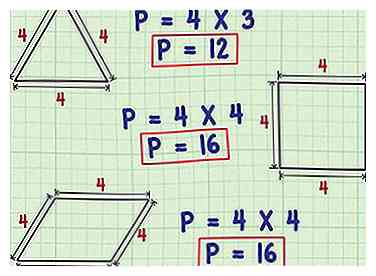 3 Multiplizieren Sie die Seitenlänge eines regulären Polygons mit der Anzahl der Seiten. Polygone, deren Seiten sind alle gleich lang und deren Winkel sind alle die gleiche Größe werden reguläre Polygone genannt. Zum Beispiel sind Quadrate und gleichseitige Dreiecke regelmäßige Polygone, ebenso wie perfekte Fünfecke (am Beispiel des Chrysler-Logos) und Achtecke (wie zum Beispiel Stopp-Zeichen). Wenn es sich bei einer Form um ein reguläres Polygon handelt, ist es einfach, die Länge einer Seite mit der Anzahl der Seiten in der Form zu multiplizieren.
3 Multiplizieren Sie die Seitenlänge eines regulären Polygons mit der Anzahl der Seiten. Polygone, deren Seiten sind alle gleich lang und deren Winkel sind alle die gleiche Größe werden reguläre Polygone genannt. Zum Beispiel sind Quadrate und gleichseitige Dreiecke regelmäßige Polygone, ebenso wie perfekte Fünfecke (am Beispiel des Chrysler-Logos) und Achtecke (wie zum Beispiel Stopp-Zeichen). Wenn es sich bei einer Form um ein reguläres Polygon handelt, ist es einfach, die Länge einer Seite mit der Anzahl der Seiten in der Form zu multiplizieren. - Zum Beispiel ist der Umfang eines perfekten Quadrats mit einer Seitenlänge von 4 Zoll (10,2 cm) 4 × 4 (weil ein Quadrat 4 Seiten hat) oder 16 Zoll (40,6 cm), während der Umfang eines gleichseitigen Dreiecks mit einer Seitenlänge von 4 Zoll (10,2 cm) 4 × 3 oder 12 Zoll (30,5 cm).
- Derselbe grundlegende Prozess funktioniert auch für nicht reguläre Polygone, deren Seiten alle gleich lang sind. Zum Beispiel, obwohl ein Rhombus kein reguläres Polygon ist, weil seine Winkel nicht alle die gleiche Größe haben, können Sie seinen Umfang finden, indem Sie die Länge einer Seite mit der Anzahl der Seiten multiplizieren, weil alle 4 seiner Seiten die gleiche Länge haben.
-
 4 Alternativ können Sie den Bereich und verwenden Apothema eines regelmäßigen Polygons, um seinen Umfang zu finden. Obwohl es einfach ist, die Länge einer der Seiten eines regulären Polygons mit der Anzahl der Seiten im Polygon zu multiplizieren, ist der einfachste Weg, den Umfang zu finden. Dies ist jedoch nicht der einzige Weg. Der Abstand von der Mitte des Polygons zur genauen Mitte einer seiner Seiten, genannt der Apothema, ist Teil einer Gleichung, die es Ihnen ermöglicht, ihren Umfang zu finden, sofern Sie auch den Bereich des Polygons kennen. Einfügen bekannter Werte für Fläche und Apothem in die Gleichung (Fläche) = (Umfang) × (Apothem) / 2 erlaubt Ihnen, mit einfachen Algebra nach dem Bereich des Polygons zu suchen.
4 Alternativ können Sie den Bereich und verwenden Apothema eines regelmäßigen Polygons, um seinen Umfang zu finden. Obwohl es einfach ist, die Länge einer der Seiten eines regulären Polygons mit der Anzahl der Seiten im Polygon zu multiplizieren, ist der einfachste Weg, den Umfang zu finden. Dies ist jedoch nicht der einzige Weg. Der Abstand von der Mitte des Polygons zur genauen Mitte einer seiner Seiten, genannt der Apothema, ist Teil einer Gleichung, die es Ihnen ermöglicht, ihren Umfang zu finden, sofern Sie auch den Bereich des Polygons kennen. Einfügen bekannter Werte für Fläche und Apothem in die Gleichung (Fläche) = (Umfang) × (Apothem) / 2 erlaubt Ihnen, mit einfachen Algebra nach dem Bereich des Polygons zu suchen. - Zum Beispiel hat das Quadrat mit einer Seitenlänge von 4 Zoll (10,2 cm) im obigen Beispiel eine Fläche von 16 Zoll2 und ein Apothem von 2 Zoll (5,1 cm). Mit unserer neuen Gleichung lösen wir den Umfang wie folgt:
- 16 = (Umfang) × 2/2
- 16 = (Umfang) × 1
- 16 = Umfang. Der Umfang des Platzes ist 16 Zoll (40,6 cm) - Dies ist die gleiche Antwort, die wir oben mit der Standardmethode erhalten haben.
- Zum Beispiel hat das Quadrat mit einer Seitenlänge von 4 Zoll (10,2 cm) im obigen Beispiel eine Fläche von 16 Zoll2 und ein Apothem von 2 Zoll (5,1 cm). Mit unserer neuen Gleichung lösen wir den Umfang wie folgt:
 Minotauromaquia
Minotauromaquia
 1 Suchen und addieren Sie die Längen aller Seiten des Polygons. Der Umfang von irgendein Das Polygon kann berechnet werden, indem man die Länge jeder Seite einzeln ermittelt und dann alle diese Längen addiert. Dies ist der einfachste Weg, den Umfang eines Polygons zu finden, und in Formen, in denen keine zwei Seiten gleich sind, ist dies normalerweise der einzig richtige Weg.
1 Suchen und addieren Sie die Längen aller Seiten des Polygons. Der Umfang von irgendein Das Polygon kann berechnet werden, indem man die Länge jeder Seite einzeln ermittelt und dann alle diese Längen addiert. Dies ist der einfachste Weg, den Umfang eines Polygons zu finden, und in Formen, in denen keine zwei Seiten gleich sind, ist dies normalerweise der einzig richtige Weg.  2 Multiplizieren Sie die Längen gleicher Seiten mit der Anzahl gleicher Seiten. Bestimmte Arten von Polygonen haben zwei oder mehr gleiche Seiten. Zum Beispiel haben gleichschenklige Dreiecke und gleichschenklige Trapeze 2 der Seiten mit der gleichen Länge, während Parallelogramme und Rechtecke 2 Paare gegenüberliegender Seiten mit gleicher Länge aufweisen. In diesen Fällen können Sie, wenn Sie die Länge einer der identischen Seiten kennen, diese Länge mit der Anzahl der Seiten multiplizieren, die diese Länge teilen, und dann die Längen aller ungleichen Seiten addieren, um den Umfang der Gesamtform zu finden.
2 Multiplizieren Sie die Längen gleicher Seiten mit der Anzahl gleicher Seiten. Bestimmte Arten von Polygonen haben zwei oder mehr gleiche Seiten. Zum Beispiel haben gleichschenklige Dreiecke und gleichschenklige Trapeze 2 der Seiten mit der gleichen Länge, während Parallelogramme und Rechtecke 2 Paare gegenüberliegender Seiten mit gleicher Länge aufweisen. In diesen Fällen können Sie, wenn Sie die Länge einer der identischen Seiten kennen, diese Länge mit der Anzahl der Seiten multiplizieren, die diese Länge teilen, und dann die Längen aller ungleichen Seiten addieren, um den Umfang der Gesamtform zu finden.  3 Multiplizieren Sie die Seitenlänge eines regulären Polygons mit der Anzahl der Seiten. Polygone, deren Seiten sind alle gleich lang und deren Winkel sind alle die gleiche Größe werden reguläre Polygone genannt. Zum Beispiel sind Quadrate und gleichseitige Dreiecke regelmäßige Polygone, ebenso wie perfekte Fünfecke (am Beispiel des Chrysler-Logos) und Achtecke (wie zum Beispiel Stopp-Zeichen). Wenn es sich bei einer Form um ein reguläres Polygon handelt, ist es einfach, die Länge einer Seite mit der Anzahl der Seiten in der Form zu multiplizieren.
3 Multiplizieren Sie die Seitenlänge eines regulären Polygons mit der Anzahl der Seiten. Polygone, deren Seiten sind alle gleich lang und deren Winkel sind alle die gleiche Größe werden reguläre Polygone genannt. Zum Beispiel sind Quadrate und gleichseitige Dreiecke regelmäßige Polygone, ebenso wie perfekte Fünfecke (am Beispiel des Chrysler-Logos) und Achtecke (wie zum Beispiel Stopp-Zeichen). Wenn es sich bei einer Form um ein reguläres Polygon handelt, ist es einfach, die Länge einer Seite mit der Anzahl der Seiten in der Form zu multiplizieren.  4 Alternativ können Sie den Bereich und verwenden Apothema eines regelmäßigen Polygons, um seinen Umfang zu finden. Obwohl es einfach ist, die Länge einer der Seiten eines regulären Polygons mit der Anzahl der Seiten im Polygon zu multiplizieren, ist der einfachste Weg, den Umfang zu finden. Dies ist jedoch nicht der einzige Weg. Der Abstand von der Mitte des Polygons zur genauen Mitte einer seiner Seiten, genannt der Apothema, ist Teil einer Gleichung, die es Ihnen ermöglicht, ihren Umfang zu finden, sofern Sie auch den Bereich des Polygons kennen. Einfügen bekannter Werte für Fläche und Apothem in die Gleichung (Fläche) = (Umfang) × (Apothem) / 2 erlaubt Ihnen, mit einfachen Algebra nach dem Bereich des Polygons zu suchen.
4 Alternativ können Sie den Bereich und verwenden Apothema eines regelmäßigen Polygons, um seinen Umfang zu finden. Obwohl es einfach ist, die Länge einer der Seiten eines regulären Polygons mit der Anzahl der Seiten im Polygon zu multiplizieren, ist der einfachste Weg, den Umfang zu finden. Dies ist jedoch nicht der einzige Weg. Der Abstand von der Mitte des Polygons zur genauen Mitte einer seiner Seiten, genannt der Apothema, ist Teil einer Gleichung, die es Ihnen ermöglicht, ihren Umfang zu finden, sofern Sie auch den Bereich des Polygons kennen. Einfügen bekannter Werte für Fläche und Apothem in die Gleichung (Fläche) = (Umfang) × (Apothem) / 2 erlaubt Ihnen, mit einfachen Algebra nach dem Bereich des Polygons zu suchen.