Diese Methode der Multiplikation und Division wurde von Descartes verwendet und stammt aus Euklids "Elements", Buch VI, Proposition 12. Sie basiert auf ähnlichen Dreiecken. Es kann sehr gut die Art sein, wie Mutter Natur Multiplikation und Division durchführt! Man stellt sich vor, dass die Natur in der Lage wäre, gerade Linien durch die Emission von schnellen Schwingungen durch dicht gepackte Teilchen oder Moleküle zu erzeugen. Sehen Sie den Artikel "Einen Kreis zentrieren" und denken Sie darüber nach, wie es umgekehrt funktionieren könnte, um genau diese Anforderung zu erfüllen. Dies ist jedoch nur eine Theorie, eine Möglichkeit; Die Wissenschaft weiß, dass die Natur mathematische Wunder wie Phyllotaxis und Wachstumsmuster ähnlich wie fraktale iterative Muster vollbringt, aber immer noch darüber diskutiert, wie sie das bewerkstelligt! Es lohnt sich, über Experimente und empirische Beweise nachzudenken und diese zu entwickeln.
Schritte
- Machen Sie sich mit dem Bild des Grundkonzepts vertraut:
 Ähnliche Dreiecke
Ähnliche Dreiecke
Erster Teil von Drei:
Das Tutorial
-
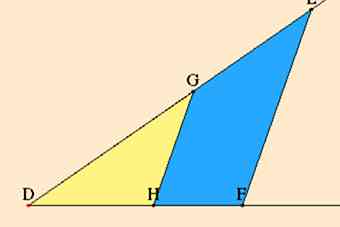
 1 Sehen Sie sich diese ähnlichen Dreiecke an, und daher das Verhältnis DG / DH = DE / DF.
1 Sehen Sie sich diese ähnlichen Dreiecke an, und daher das Verhältnis DG / DH = DE / DF.  Ähnliche Dreiecke Sie können damit Multiplikation und Division durchführen. Öffnen Sie eine neue Arbeitsmappe in Excel, und kopieren Sie die Zeichnung.
Ähnliche Dreiecke Sie können damit Multiplikation und Division durchführen. Öffnen Sie eine neue Arbeitsmappe in Excel, und kopieren Sie die Zeichnung. - 2 Um x mal y zu multiplizieren, führe die horizontale Linie DH der Länge 1 aus, erweitere die DF der Länge x von DH und erhöhe die DG der Länge y in einem Winkel über der horizontalen DF. Zeichne HG und konstruiere eine Linie durch F parallel zu HG. Lass es DG bei E schneiden. Dann wird DE die Länge xy haben.
- 3 Um y durch x zu teilen, mache DH mit der Länge 1, DF mit der Länge x und DE mit der Länge y. Zeichne EF und konstruiere eine Linie durch H parallel zu EF. Lass es DE bei G schneiden. Dann wird DG die Länge y / x haben.
- 4 Angenommen, ein Stamm oder Blatt liegt unter einem anderen, in seinem Schatten. Wäre dies möglicherweise eine Möglichkeit, Zeit zu behalten und zu wissen, wann man sich zur Seite bewegen sollte, um direkt ein besseres Licht für das untere Blatt oder den unteren Stamm zu erhalten?
- 5 Angenommen, man kreuzt Wurzeln (was sie tun) und nehmen gewisse Empfindlichkeiten für einander an - könnte dies eine Art sein, wie Pflanzen Mathematik ausführen und lebenswichtige Nährstoffe rechtzeitig an die Pflanzen schicken? Schließlich sind die Wurzeln im Dunkeln, woher wissen sie, wie spät es ist oder berechnen Sie den Anteil einer bestimmten chemischen Beimengung zu senden?
- 6 Angenommen, Neuronen, die sich in verschiedenen Winkeln im Gehirn verzweigen (was sie tun) - könnte dies eine Möglichkeit zur Berechnung von p / n = A.E.N sein. (Fast jede Nummer)? Das heißt, fast jede Zahl kann als ein Quotient zweier anderer Zahlen ausgedrückt werden, z. 36/2 = 18 und 625/256 = 2,44140625 oder 5 ^ 4/4 ^ 4 oder 5/4 ^ (1 / (5/4 - 1)). Siehe die Artikel Beginnen Sie mit fortlaufenden Brüchen zu arbeiten und lösen Sie aB = a ^ B in neutralen Operationen mit Algebra, wo E = mc ^ n diskutiert wird, wenn sich n nähert. 2. Ist es möglich, Gestern im Speicher zu sehen, indem Sie langsamer als angehaltene Zeit sehen bei Lichtgeschwindigkeit im Quadrat? Ist die "Vergangenheit" auf der Gegenseite aller Elektronen, die mir gegenüber stehen, und die "Zukunft", die sich von dieser entgegengesetzten Position aus dreht, um mich auch zu begrüßen? Das würde die unmittelbare Vergangenheit der unmittelbaren Zukunft sehr ähnlich machen und zu einem ziemlich stabilen Geschenk führen. Und geometrisch würden alle Strahlen von allen Teilchen, die in Schwingungen durchkommen, ziemlich konstant multipliziert und auch geteilt werden, solange man ziemlich ruhig ist, oder in einer relativ stabilen Umgebung. Nennen Sie das "Die Annahme über Neuronen und Neutronen", wenn Sie möchten.
- 7Descartes verwendete auch den nächsten Satz VI.13, um geometrisch Quadratwurzeln zu nehmen.
Zweiter Teil von Drei:
Bleib neugierig
- 1 Wenn es geometrisch gemacht werden kann, kann Mutter Natur es innerhalb vernünftiger Toleranzen durchführen? Das heißt, kann sie vernünftige Schätzungen der Quadratwurzel oder einer beliebigen Wurzel einer Zahl erhalten? Man vermutet "jede Wurzel" von einem iterativen Prozess (der Euklid, Descartes oder Newton-Raphson offenbar nicht vorkam).
- 2 Endgültiges Bild:
 Ähnliche Dreiecke
Ähnliche Dreiecke
Teil drei von drei:
Hilfreiche Anleitung
- 1 Verwenden Sie Hilfsartikel, wenn Sie dieses Tutorial durcharbeiten:
- Eine Liste von Artikeln zu Excel, Geometrischer und / oder Trigonometrischer Kunst, Diagrammerstellung und algebraischer Formulierung finden Sie im Artikel Erstellen eines spiralförmigen Spinpartikel-Pfads oder einer Kettenform oder eines sphärischen Rahmens.
- Für weitere Diagramme und Diagramme, klicken Sie auf Kategorie: Microsoft Excel Bilder, Kategorie: Mathematik, Kategorie: Tabellenkalkulation oder Kategorie: Grafiken, um viele Excel Arbeitsblätter und Diagramme zu sehen, in denen Trigonometrie, Geometrie und Kalkül in Kunst umgewandelt wurden, oder klicken Sie einfach auf die Kategorie wie oben rechts auf der Seite oder links unten auf der Seite.
 Minotauromaquia
Minotauromaquia

 1 Sehen Sie sich diese ähnlichen Dreiecke an, und daher das Verhältnis DG / DH = DE / DF.
1 Sehen Sie sich diese ähnlichen Dreiecke an, und daher das Verhältnis DG / DH = DE / DF.