Ähnliche Dreiecke sind zwei Dreiecke, die die gleichen Winkel und entsprechende Seiten haben, die gleiche Proportionen haben.[1] Das Nachweisen ähnlicher Dreiecke bezieht sich auf einen geometrischen Prozess, mit dem Sie nachweisen können, dass zwei Dreiecke genügend Gemeinsamkeiten aufweisen, um als ähnlich angesehen zu werden. Mit einfachen geometrischen Theoremen können Sie leicht beweisen, dass zwei Dreiecke ähnlich sind.
Teil eins von vier:
Verwenden des Winkel-Winkel-Satzes
-
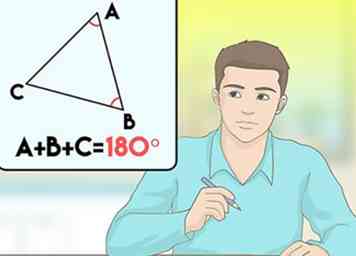 1 Definieren Sie das Winkel-Winkel (AA) Theorem. Zwei Dreiecke können durch den Winkel-Winkel-Satz ähnlich bewiesen werden: Wenn zwei Dreiecke zwei kongruente Winkel haben, dann sind diese Dreiecke ähnlich.
1 Definieren Sie das Winkel-Winkel (AA) Theorem. Zwei Dreiecke können durch den Winkel-Winkel-Satz ähnlich bewiesen werden: Wenn zwei Dreiecke zwei kongruente Winkel haben, dann sind diese Dreiecke ähnlich. - Dieser Satz wird auch als Winkel-Winkel-Winkel-Satz (AAA) bezeichnet, weil, wenn zwei Winkel des Dreiecks kongruent sind, der dritte Winkel ebenfalls kongruent sein muss. Dies liegt daran, dass die Winkel eines Dreiecks sich zu 180 ° addieren müssen.[2]
-
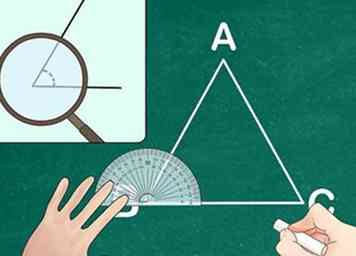 2 Identifizieren Sie das Maß von mindestens zwei Winkeln in einem der Dreiecke. Mit einem Winkelmesser den Grad von mindestens zwei Winkeln auf dem ersten Dreieck messen. Beschriften Sie die Winkel auf dem Dreieck, um sie zu verfolgen.
2 Identifizieren Sie das Maß von mindestens zwei Winkeln in einem der Dreiecke. Mit einem Winkelmesser den Grad von mindestens zwei Winkeln auf dem ersten Dreieck messen. Beschriften Sie die Winkel auf dem Dreieck, um sie zu verfolgen. - Wählen Sie zwei beliebige Winkel auf dem zu messenden Dreieck.
- Beispiel: Dreieck ABC hat zwei Winkel, die 30 ° und 70 ° messen.
-
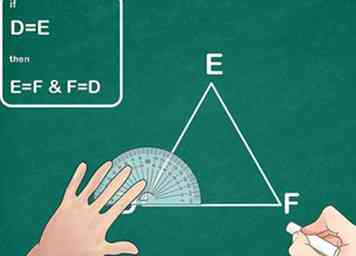 3 Messen Sie mindestens zwei der Winkel des zweiten Dreiecks. Verwenden Sie erneut einen Winkelmesser, um zwei der Winkel des zweiten Dreiecks zu messen. Wenn beide Winkel in beiden Dreiecken identisch sind, sind die Dreiecke einander ähnlich.
3 Messen Sie mindestens zwei der Winkel des zweiten Dreiecks. Verwenden Sie erneut einen Winkelmesser, um zwei der Winkel des zweiten Dreiecks zu messen. Wenn beide Winkel in beiden Dreiecken identisch sind, sind die Dreiecke einander ähnlich. - Denken Sie daran, wenn zwei Winkel eines Dreiecks gleich sind, dann sind alle drei gleich.
- Beispiel: Das zweite Dreieck, DEF, hat ebenfalls zwei Winkel, die 30 ° und 70 ° messen.
-
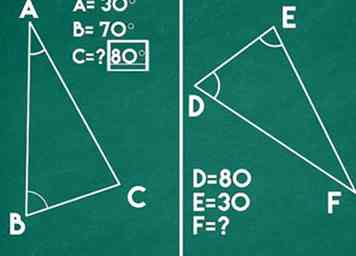 4 Verwenden Sie das Winkel-Winkel-Theorem für Ähnlichkeit. Sobald Sie die kongruenten Winkel identifiziert haben, können Sie diesen Satz verwenden, um zu beweisen, dass die Dreiecke ähnlich sind. Stellen Sie fest, dass die Maße der Winkel zwischen den beiden Dreiecken identisch sind, und geben Sie den Winkel-Winkel-Satz als Beweis für ihre Ähnlichkeit an.[3]
4 Verwenden Sie das Winkel-Winkel-Theorem für Ähnlichkeit. Sobald Sie die kongruenten Winkel identifiziert haben, können Sie diesen Satz verwenden, um zu beweisen, dass die Dreiecke ähnlich sind. Stellen Sie fest, dass die Maße der Winkel zwischen den beiden Dreiecken identisch sind, und geben Sie den Winkel-Winkel-Satz als Beweis für ihre Ähnlichkeit an.[3] - Es ist möglich, dass ein Dreieck mit drei identischen Winkeln auch kongruent ist, aber auch identische Seitenlängen haben müssten.
- Beispiel: Da beide Dreiecke zwei identische Winkel haben, sind sie ähnlich.
- Hinweis: Wenn die zwei Dreiecke nicht identische Winkel hätten, wären sie nicht ähnlich. Zum Beispiel: Dreieck ABC hat Winkel von 30 ° und 70 ° und Dreieck DEF hat Winkel von 35 ° und 70 °. Weil 30 ° nicht gleich 35 ° ist, sind die Dreiecke nicht ähnlich.
Teil zwei von vier:
Verwenden des Side-Angle-Side Theorems
-
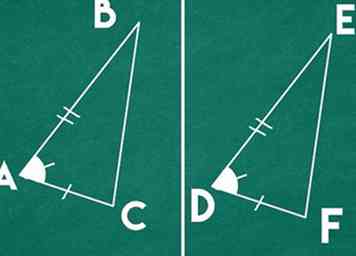 1 Definieren Sie den Side-Angle-Side (SAS) Theorem für Ähnlichkeit. Wenn ein Dreieck zwei Seiten hat, die im gleichen Verhältnis zu einem anderen Dreieck stehen und deren eingeschlossener Winkel gleich ist, sind diese Dreiecke ähnlich.[4]
1 Definieren Sie den Side-Angle-Side (SAS) Theorem für Ähnlichkeit. Wenn ein Dreieck zwei Seiten hat, die im gleichen Verhältnis zu einem anderen Dreieck stehen und deren eingeschlossener Winkel gleich ist, sind diese Dreiecke ähnlich.[4] - Achten Sie darauf, diesen Satz nicht mit dem Kongruenzsatz für die Seite-Winkel-Seite zu verwechseln. Zur Kongruenz müssen die beiden Seiten mit ihrem eingeschlossenen Winkel identisch sein; für die Ähnlichkeit müssen die Proportionen der Seiten gleich sein und der Winkel muss identisch sein.
- Zum Beispiel: Dreieck ABC und DEF sind ähnlich ist Winkel A = Winkel D und AB / DE = AC / DF.
-
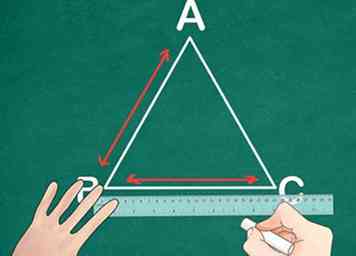 2 Messen Sie die gleichen zwei Seiten jeder Dreiecke. Messen Sie mit einem Lineal zwei Seiten des Dreiecks ABC und beschriften Sie sie mit diesem Maß. Stellen Sie sicher, dass das Dreieck DEF in derselben Richtung ausgerichtet ist und messen Sie die gleichen zwei Seiten. Beschriften Sie auch diese Seiten.
2 Messen Sie die gleichen zwei Seiten jeder Dreiecke. Messen Sie mit einem Lineal zwei Seiten des Dreiecks ABC und beschriften Sie sie mit diesem Maß. Stellen Sie sicher, dass das Dreieck DEF in derselben Richtung ausgerichtet ist und messen Sie die gleichen zwei Seiten. Beschriften Sie auch diese Seiten. - Beispiel: Maße des Dreiecks ABC; Seite AB = 4 cm und Seite AC = 8 cm. Maße des Dreiecks DEF; Seite DE = 2 cm und Seite DF = 4 cm.
-
 3 Identifizieren Sie das Maß für den Winkel zwischen diesen beiden Seiten. Messen Sie mit einem Winkelmesser den eingeschlossenen Winkel oder den Winkel zwischen den beiden Seiten, die Sie bereits gemessen haben. Für diesen Satz sollte das Maß des Winkels in beiden Dreiecken identisch sein.
3 Identifizieren Sie das Maß für den Winkel zwischen diesen beiden Seiten. Messen Sie mit einem Winkelmesser den eingeschlossenen Winkel oder den Winkel zwischen den beiden Seiten, die Sie bereits gemessen haben. Für diesen Satz sollte das Maß des Winkels in beiden Dreiecken identisch sein. - Beispiel: Winkel A im Dreieck ABC ist 26 °. Der Winkel D im Dreieck DEF beträgt ebenfalls 26 °.
-
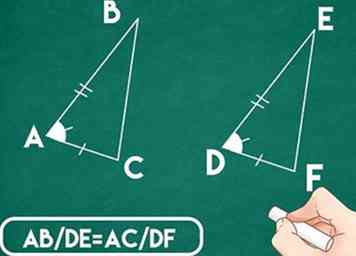 4 Berechnen Sie den Anteil der Seitenlängen zwischen den beiden Dreiecken. Um das SAS-Theorem zu verwenden, müssen die Seiten der Dreiecke proportional zueinander sein. Um dies zu berechnen, verwenden Sie einfach die Formel AB / DE = AC / DF.
4 Berechnen Sie den Anteil der Seitenlängen zwischen den beiden Dreiecken. Um das SAS-Theorem zu verwenden, müssen die Seiten der Dreiecke proportional zueinander sein. Um dies zu berechnen, verwenden Sie einfach die Formel AB / DE = AC / DF. - Beispiel: AB / DE = AC / DF; 4/2 = 8/4; 2 = 2. Die Proportionen der zwei Dreiecke sind gleich.
-
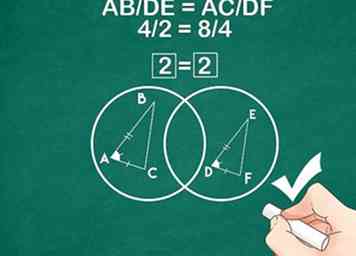 5 Wenden Sie das Side-Angle-Side Theorem an, um die Ähnlichkeit nachzuweisen. Sobald Sie festgestellt haben, dass die Proportionen von zwei Seiten eines Dreiecks und ihr eingeschlossener Winkel gleich sind, können Sie das SAS-Theorem in Ihrem Beweis verwenden.
5 Wenden Sie das Side-Angle-Side Theorem an, um die Ähnlichkeit nachzuweisen. Sobald Sie festgestellt haben, dass die Proportionen von zwei Seiten eines Dreiecks und ihr eingeschlossener Winkel gleich sind, können Sie das SAS-Theorem in Ihrem Beweis verwenden. - Beispiel: Da AB / DE = AAC / DF und Winkel A = Winkel D ist, ist das Dreieck ABC ähnlich dem Dreieck DEF.
- Hinweis: Wenn Winkel A nicht gleich Winkel D wäre, wären die Dreiecke nicht ähnlich. Auch wenn die Proportionen nicht gleich wären, wären die Dreiecke nicht ähnlich.
Teil drei von vier:
Verwenden des Side-Side-Side-Theorems
-
 1 Definieren Sie den Side-Side-Side (SSS) Theorem für Ähnlichkeit. Zwei Dreiecke würden als ähnlich betrachtet, wenn die drei Seiten beider Dreiecke das gleiche Verhältnis haben. Seiten, die 2: 4: 6 und 4: 8: 12 messen, würden Beweis der Ähnlichkeit liefern.
1 Definieren Sie den Side-Side-Side (SSS) Theorem für Ähnlichkeit. Zwei Dreiecke würden als ähnlich betrachtet, wenn die drei Seiten beider Dreiecke das gleiche Verhältnis haben. Seiten, die 2: 4: 6 und 4: 8: 12 messen, würden Beweis der Ähnlichkeit liefern. - Seien Sie vorsichtig, diesen Satz nicht mit dem Side-Side-Side-Theorem für Kongruenz zu verwechseln: Wenn zwei Dreiecke drei identische Seiten haben, sind sie kongruent. Der Theorem für Ähnlichkeit behandelt streng die Proportionen der drei Seiten.
- Zum Beispiel: Im Dreieck ABC und DEF sind die Dreiecke ähnlich, wenn AB / DE = AC / DF = BC / EF.
-
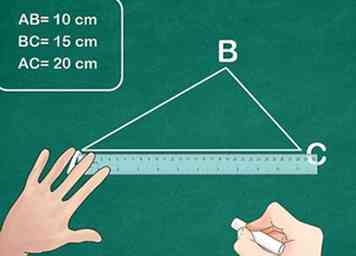 2 Messen Sie die Seiten jedes Dreiecks. Messen Sie mit einem Lineal alle drei Seiten jedes Dreiecks. Beschriften Sie jede Seite, um alle Messungen zu verfolgen. Stellen Sie sicher, dass Sie für jede Messung der Seiten des Dreiecks die gleichen Einheiten verwenden.
2 Messen Sie die Seiten jedes Dreiecks. Messen Sie mit einem Lineal alle drei Seiten jedes Dreiecks. Beschriften Sie jede Seite, um alle Messungen zu verfolgen. Stellen Sie sicher, dass Sie für jede Messung der Seiten des Dreiecks die gleichen Einheiten verwenden. - Beispiel: Dreieck ABC hat Seiten AB = 10 cm, BC = 15 cm, AC = 20 cm und Dreieck DEF hat Seiten DE = 2 cm, EF = 3 cm und DF = 4 cm.
-
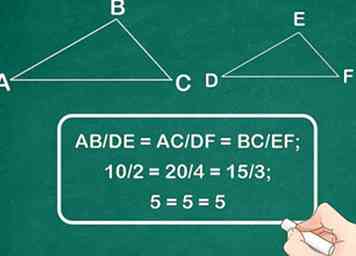 3 Berechnen Sie die Proportionen zwischen den Seiten jedes Dreiecks. Damit das SSS-Theorem anwendbar ist, müssen die drei Seiten jedes Dreiecks proportional zueinander sein. Berechnen Sie die Proportionen mit den Seitenmaßen nach der Formel AB / DE = AC / DF = BC / EF.[5]
3 Berechnen Sie die Proportionen zwischen den Seiten jedes Dreiecks. Damit das SSS-Theorem anwendbar ist, müssen die drei Seiten jedes Dreiecks proportional zueinander sein. Berechnen Sie die Proportionen mit den Seitenmaßen nach der Formel AB / DE = AC / DF = BC / EF.[5] - Beispiel: AB / DE = AC / DF = BC / EF; 10/2 = 20/4 = 15/3; 5 = 5 = 5.
-
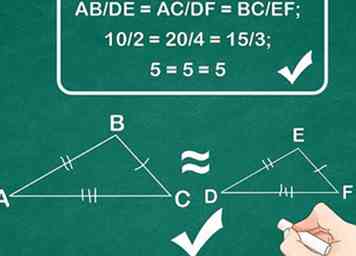 4 Wenden Sie das Side-Side-Side-Theorem an, um Ähnlichkeit zu beweisen. Wenn Sie festgestellt haben, dass die Proportionen aller drei Seiten der Dreiecke gleich sind, können Sie das SSS-Theorem verwenden, um zu beweisen, dass diese Dreiecke ähnlich sind.[6]
4 Wenden Sie das Side-Side-Side-Theorem an, um Ähnlichkeit zu beweisen. Wenn Sie festgestellt haben, dass die Proportionen aller drei Seiten der Dreiecke gleich sind, können Sie das SSS-Theorem verwenden, um zu beweisen, dass diese Dreiecke ähnlich sind.[6] - Beispiel: Da AB / DE = AC / DF = BC / EF, sind Dreieck ABC und Dreieck DEF ähnlich.
- Hinweis: Wenn AB / DE ≠ AC / DF ≠ BC / EF, dann wären die Dreiecke nicht ähnlich.
Teil vier von vier:
Einen Beweis schreiben
-
 1 Studieren Sie das Format eines formalen Beweises. Ein Beweis beginnt mit einer Aussage gegebener Information, die als Hypothesen-Aussage bekannt ist. Sie müssen eine Liste relevanter Informationen sowie Hinweise zur Unterstützung jeder Aussage bereitstellen.
1 Studieren Sie das Format eines formalen Beweises. Ein Beweis beginnt mit einer Aussage gegebener Information, die als Hypothesen-Aussage bekannt ist. Sie müssen eine Liste relevanter Informationen sowie Hinweise zur Unterstützung jeder Aussage bereitstellen. -
 2 Entwickeln Sie eine Hypothese, um das Problem zu lösen, oder vervollständigen Sie den Beweis. Sie müssen ein Diagramm erstellen, das in der Regel zwei Spalten enthält. Diese erste Spalte enthält Ihre Aussagen, während die zweite Ihre Beweise enthält.[7]
2 Entwickeln Sie eine Hypothese, um das Problem zu lösen, oder vervollständigen Sie den Beweis. Sie müssen ein Diagramm erstellen, das in der Regel zwei Spalten enthält. Diese erste Spalte enthält Ihre Aussagen, während die zweite Ihre Beweise enthält.[7] - Stellen Sie sicher, dass die letzte Zeile in Ihrer Anweisungsspalte immer mit der Hypothese übereinstimmt. In den mittleren Zeilen werden Sie Ihre Arbeit zeigen, während Sie das Problem lösen. Alle von Ihnen zur Verfügung gestellten Aussagen sowie Ihre unterstützenden Nachweise sollten immer auf die Zahlen verweisen, die in der Hypothesen-Erklärung beschrieben sind.
-
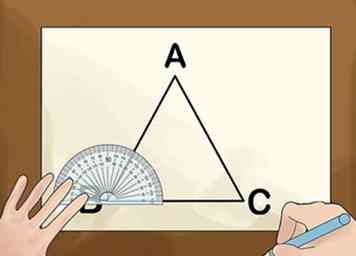 3 Zeichnen Sie ein Diagramm der Figuren, die in der Hypothese beschrieben sind, wenn eine Illustration nicht bereits zur Verfügung gestellt wurde. Verwenden Sie alle Details, die von der Hypothese geliefert werden. Achten Sie darauf, die Figur groß genug zu zeichnen, damit Sie diese Details leicht erkennen können. Beschriften Sie alle beschriebenen Punkte und stellen Sie sicher, dass Sie Informationen aus der Aussage zu parallelen Linien oder kongruenten Winkeln enthalten.
3 Zeichnen Sie ein Diagramm der Figuren, die in der Hypothese beschrieben sind, wenn eine Illustration nicht bereits zur Verfügung gestellt wurde. Verwenden Sie alle Details, die von der Hypothese geliefert werden. Achten Sie darauf, die Figur groß genug zu zeichnen, damit Sie diese Details leicht erkennen können. Beschriften Sie alle beschriebenen Punkte und stellen Sie sicher, dass Sie Informationen aus der Aussage zu parallelen Linien oder kongruenten Winkeln enthalten. -
 4 Schreiben Sie die gegebenen Informationen auf. Für jedes Problem erhalten Sie einige Informationen über die Maße der Winkel und der Seiten der beiden Dreiecke, die Sie ähnlich zu beweisen versuchen. Der erste Schritt zur Identifizierung des richtigen zu verwendenden Theorems ist das Aufschreiben der Informationen, die Sie bereits kennen.
4 Schreiben Sie die gegebenen Informationen auf. Für jedes Problem erhalten Sie einige Informationen über die Maße der Winkel und der Seiten der beiden Dreiecke, die Sie ähnlich zu beweisen versuchen. Der erste Schritt zur Identifizierung des richtigen zu verwendenden Theorems ist das Aufschreiben der Informationen, die Sie bereits kennen. - Wenn kein Diagramm vorhanden ist, zeichnen Sie die Dreiecke und beschriften Sie deren Winkel und Seiten mit den angegebenen Informationen.
-
 5 Wählen Sie den Satz, der zu den gegebenen Informationen passt. Sobald Sie Ihre gegebenen Informationen niedergeschrieben und die drei möglichen Sätze gelernt haben, die sich anwenden lassen könnten, wählen Sie diejenige, die den gegebenen Informationen entspricht. Es ist in Ordnung, wenn mehrere Sätze gelten, wählen Sie einfach einen für Ihren Beweis.
5 Wählen Sie den Satz, der zu den gegebenen Informationen passt. Sobald Sie Ihre gegebenen Informationen niedergeschrieben und die drei möglichen Sätze gelernt haben, die sich anwenden lassen könnten, wählen Sie diejenige, die den gegebenen Informationen entspricht. Es ist in Ordnung, wenn mehrere Sätze gelten, wählen Sie einfach einen für Ihren Beweis. - Wenn keiner dieser Sätze mit den gegebenen Informationen übereinstimmt, sind die Dreiecke nicht ähnlich.
-
 6 Schreiben Sie den Beweis. Entwerfen Sie eine Strategie, um den Beweis zu lösen. Es gibt drei verschiedene Postulate oder mathematische Theorien, die für ähnliche Dreiecke gelten. Jeder von diesen wird ausreichende Beweise liefern, um zu beweisen, dass die fraglichen Dreiecke ähnlich sind.
6 Schreiben Sie den Beweis. Entwerfen Sie eine Strategie, um den Beweis zu lösen. Es gibt drei verschiedene Postulate oder mathematische Theorien, die für ähnliche Dreiecke gelten. Jeder von diesen wird ausreichende Beweise liefern, um zu beweisen, dass die fraglichen Dreiecke ähnlich sind. - Sammeln Sie Ihre Gegebenheiten und relevanten Sätze und schreiben Sie den Beweis Schritt für Schritt.
 Minotauromaquia
Minotauromaquia
 1 Definieren Sie das Winkel-Winkel (AA) Theorem. Zwei Dreiecke können durch den Winkel-Winkel-Satz ähnlich bewiesen werden: Wenn zwei Dreiecke zwei kongruente Winkel haben, dann sind diese Dreiecke ähnlich.
1 Definieren Sie das Winkel-Winkel (AA) Theorem. Zwei Dreiecke können durch den Winkel-Winkel-Satz ähnlich bewiesen werden: Wenn zwei Dreiecke zwei kongruente Winkel haben, dann sind diese Dreiecke ähnlich.  2 Identifizieren Sie das Maß von mindestens zwei Winkeln in einem der Dreiecke. Mit einem Winkelmesser den Grad von mindestens zwei Winkeln auf dem ersten Dreieck messen. Beschriften Sie die Winkel auf dem Dreieck, um sie zu verfolgen.
2 Identifizieren Sie das Maß von mindestens zwei Winkeln in einem der Dreiecke. Mit einem Winkelmesser den Grad von mindestens zwei Winkeln auf dem ersten Dreieck messen. Beschriften Sie die Winkel auf dem Dreieck, um sie zu verfolgen.  3 Messen Sie mindestens zwei der Winkel des zweiten Dreiecks. Verwenden Sie erneut einen Winkelmesser, um zwei der Winkel des zweiten Dreiecks zu messen. Wenn beide Winkel in beiden Dreiecken identisch sind, sind die Dreiecke einander ähnlich.
3 Messen Sie mindestens zwei der Winkel des zweiten Dreiecks. Verwenden Sie erneut einen Winkelmesser, um zwei der Winkel des zweiten Dreiecks zu messen. Wenn beide Winkel in beiden Dreiecken identisch sind, sind die Dreiecke einander ähnlich.  4 Verwenden Sie das Winkel-Winkel-Theorem für Ähnlichkeit. Sobald Sie die kongruenten Winkel identifiziert haben, können Sie diesen Satz verwenden, um zu beweisen, dass die Dreiecke ähnlich sind. Stellen Sie fest, dass die Maße der Winkel zwischen den beiden Dreiecken identisch sind, und geben Sie den Winkel-Winkel-Satz als Beweis für ihre Ähnlichkeit an.[3]
4 Verwenden Sie das Winkel-Winkel-Theorem für Ähnlichkeit. Sobald Sie die kongruenten Winkel identifiziert haben, können Sie diesen Satz verwenden, um zu beweisen, dass die Dreiecke ähnlich sind. Stellen Sie fest, dass die Maße der Winkel zwischen den beiden Dreiecken identisch sind, und geben Sie den Winkel-Winkel-Satz als Beweis für ihre Ähnlichkeit an.[3]  1 Definieren Sie den Side-Angle-Side (SAS) Theorem für Ähnlichkeit. Wenn ein Dreieck zwei Seiten hat, die im gleichen Verhältnis zu einem anderen Dreieck stehen und deren eingeschlossener Winkel gleich ist, sind diese Dreiecke ähnlich.[4]
1 Definieren Sie den Side-Angle-Side (SAS) Theorem für Ähnlichkeit. Wenn ein Dreieck zwei Seiten hat, die im gleichen Verhältnis zu einem anderen Dreieck stehen und deren eingeschlossener Winkel gleich ist, sind diese Dreiecke ähnlich.[4]  2 Messen Sie die gleichen zwei Seiten jeder Dreiecke. Messen Sie mit einem Lineal zwei Seiten des Dreiecks ABC und beschriften Sie sie mit diesem Maß. Stellen Sie sicher, dass das Dreieck DEF in derselben Richtung ausgerichtet ist und messen Sie die gleichen zwei Seiten. Beschriften Sie auch diese Seiten.
2 Messen Sie die gleichen zwei Seiten jeder Dreiecke. Messen Sie mit einem Lineal zwei Seiten des Dreiecks ABC und beschriften Sie sie mit diesem Maß. Stellen Sie sicher, dass das Dreieck DEF in derselben Richtung ausgerichtet ist und messen Sie die gleichen zwei Seiten. Beschriften Sie auch diese Seiten.  3 Identifizieren Sie das Maß für den Winkel zwischen diesen beiden Seiten. Messen Sie mit einem Winkelmesser den eingeschlossenen Winkel oder den Winkel zwischen den beiden Seiten, die Sie bereits gemessen haben. Für diesen Satz sollte das Maß des Winkels in beiden Dreiecken identisch sein.
3 Identifizieren Sie das Maß für den Winkel zwischen diesen beiden Seiten. Messen Sie mit einem Winkelmesser den eingeschlossenen Winkel oder den Winkel zwischen den beiden Seiten, die Sie bereits gemessen haben. Für diesen Satz sollte das Maß des Winkels in beiden Dreiecken identisch sein.  4 Berechnen Sie den Anteil der Seitenlängen zwischen den beiden Dreiecken. Um das SAS-Theorem zu verwenden, müssen die Seiten der Dreiecke proportional zueinander sein. Um dies zu berechnen, verwenden Sie einfach die Formel AB / DE = AC / DF.
4 Berechnen Sie den Anteil der Seitenlängen zwischen den beiden Dreiecken. Um das SAS-Theorem zu verwenden, müssen die Seiten der Dreiecke proportional zueinander sein. Um dies zu berechnen, verwenden Sie einfach die Formel AB / DE = AC / DF.  5 Wenden Sie das Side-Angle-Side Theorem an, um die Ähnlichkeit nachzuweisen. Sobald Sie festgestellt haben, dass die Proportionen von zwei Seiten eines Dreiecks und ihr eingeschlossener Winkel gleich sind, können Sie das SAS-Theorem in Ihrem Beweis verwenden.
5 Wenden Sie das Side-Angle-Side Theorem an, um die Ähnlichkeit nachzuweisen. Sobald Sie festgestellt haben, dass die Proportionen von zwei Seiten eines Dreiecks und ihr eingeschlossener Winkel gleich sind, können Sie das SAS-Theorem in Ihrem Beweis verwenden.  1 Definieren Sie den Side-Side-Side (SSS) Theorem für Ähnlichkeit. Zwei Dreiecke würden als ähnlich betrachtet, wenn die drei Seiten beider Dreiecke das gleiche Verhältnis haben. Seiten, die 2: 4: 6 und 4: 8: 12 messen, würden Beweis der Ähnlichkeit liefern.
1 Definieren Sie den Side-Side-Side (SSS) Theorem für Ähnlichkeit. Zwei Dreiecke würden als ähnlich betrachtet, wenn die drei Seiten beider Dreiecke das gleiche Verhältnis haben. Seiten, die 2: 4: 6 und 4: 8: 12 messen, würden Beweis der Ähnlichkeit liefern.  2 Messen Sie die Seiten jedes Dreiecks. Messen Sie mit einem Lineal alle drei Seiten jedes Dreiecks. Beschriften Sie jede Seite, um alle Messungen zu verfolgen. Stellen Sie sicher, dass Sie für jede Messung der Seiten des Dreiecks die gleichen Einheiten verwenden.
2 Messen Sie die Seiten jedes Dreiecks. Messen Sie mit einem Lineal alle drei Seiten jedes Dreiecks. Beschriften Sie jede Seite, um alle Messungen zu verfolgen. Stellen Sie sicher, dass Sie für jede Messung der Seiten des Dreiecks die gleichen Einheiten verwenden.  3 Berechnen Sie die Proportionen zwischen den Seiten jedes Dreiecks. Damit das SSS-Theorem anwendbar ist, müssen die drei Seiten jedes Dreiecks proportional zueinander sein. Berechnen Sie die Proportionen mit den Seitenmaßen nach der Formel AB / DE = AC / DF = BC / EF.[5]
3 Berechnen Sie die Proportionen zwischen den Seiten jedes Dreiecks. Damit das SSS-Theorem anwendbar ist, müssen die drei Seiten jedes Dreiecks proportional zueinander sein. Berechnen Sie die Proportionen mit den Seitenmaßen nach der Formel AB / DE = AC / DF = BC / EF.[5]  4 Wenden Sie das Side-Side-Side-Theorem an, um Ähnlichkeit zu beweisen. Wenn Sie festgestellt haben, dass die Proportionen aller drei Seiten der Dreiecke gleich sind, können Sie das SSS-Theorem verwenden, um zu beweisen, dass diese Dreiecke ähnlich sind.[6]
4 Wenden Sie das Side-Side-Side-Theorem an, um Ähnlichkeit zu beweisen. Wenn Sie festgestellt haben, dass die Proportionen aller drei Seiten der Dreiecke gleich sind, können Sie das SSS-Theorem verwenden, um zu beweisen, dass diese Dreiecke ähnlich sind.[6]  1 Studieren Sie das Format eines formalen Beweises. Ein Beweis beginnt mit einer Aussage gegebener Information, die als Hypothesen-Aussage bekannt ist. Sie müssen eine Liste relevanter Informationen sowie Hinweise zur Unterstützung jeder Aussage bereitstellen.
1 Studieren Sie das Format eines formalen Beweises. Ein Beweis beginnt mit einer Aussage gegebener Information, die als Hypothesen-Aussage bekannt ist. Sie müssen eine Liste relevanter Informationen sowie Hinweise zur Unterstützung jeder Aussage bereitstellen.  2 Entwickeln Sie eine Hypothese, um das Problem zu lösen, oder vervollständigen Sie den Beweis. Sie müssen ein Diagramm erstellen, das in der Regel zwei Spalten enthält. Diese erste Spalte enthält Ihre Aussagen, während die zweite Ihre Beweise enthält.[7]
2 Entwickeln Sie eine Hypothese, um das Problem zu lösen, oder vervollständigen Sie den Beweis. Sie müssen ein Diagramm erstellen, das in der Regel zwei Spalten enthält. Diese erste Spalte enthält Ihre Aussagen, während die zweite Ihre Beweise enthält.[7]  3 Zeichnen Sie ein Diagramm der Figuren, die in der Hypothese beschrieben sind, wenn eine Illustration nicht bereits zur Verfügung gestellt wurde. Verwenden Sie alle Details, die von der Hypothese geliefert werden. Achten Sie darauf, die Figur groß genug zu zeichnen, damit Sie diese Details leicht erkennen können. Beschriften Sie alle beschriebenen Punkte und stellen Sie sicher, dass Sie Informationen aus der Aussage zu parallelen Linien oder kongruenten Winkeln enthalten.
3 Zeichnen Sie ein Diagramm der Figuren, die in der Hypothese beschrieben sind, wenn eine Illustration nicht bereits zur Verfügung gestellt wurde. Verwenden Sie alle Details, die von der Hypothese geliefert werden. Achten Sie darauf, die Figur groß genug zu zeichnen, damit Sie diese Details leicht erkennen können. Beschriften Sie alle beschriebenen Punkte und stellen Sie sicher, dass Sie Informationen aus der Aussage zu parallelen Linien oder kongruenten Winkeln enthalten.  4 Schreiben Sie die gegebenen Informationen auf. Für jedes Problem erhalten Sie einige Informationen über die Maße der Winkel und der Seiten der beiden Dreiecke, die Sie ähnlich zu beweisen versuchen. Der erste Schritt zur Identifizierung des richtigen zu verwendenden Theorems ist das Aufschreiben der Informationen, die Sie bereits kennen.
4 Schreiben Sie die gegebenen Informationen auf. Für jedes Problem erhalten Sie einige Informationen über die Maße der Winkel und der Seiten der beiden Dreiecke, die Sie ähnlich zu beweisen versuchen. Der erste Schritt zur Identifizierung des richtigen zu verwendenden Theorems ist das Aufschreiben der Informationen, die Sie bereits kennen.  5 Wählen Sie den Satz, der zu den gegebenen Informationen passt. Sobald Sie Ihre gegebenen Informationen niedergeschrieben und die drei möglichen Sätze gelernt haben, die sich anwenden lassen könnten, wählen Sie diejenige, die den gegebenen Informationen entspricht. Es ist in Ordnung, wenn mehrere Sätze gelten, wählen Sie einfach einen für Ihren Beweis.
5 Wählen Sie den Satz, der zu den gegebenen Informationen passt. Sobald Sie Ihre gegebenen Informationen niedergeschrieben und die drei möglichen Sätze gelernt haben, die sich anwenden lassen könnten, wählen Sie diejenige, die den gegebenen Informationen entspricht. Es ist in Ordnung, wenn mehrere Sätze gelten, wählen Sie einfach einen für Ihren Beweis.  6 Schreiben Sie den Beweis. Entwerfen Sie eine Strategie, um den Beweis zu lösen. Es gibt drei verschiedene Postulate oder mathematische Theorien, die für ähnliche Dreiecke gelten. Jeder von diesen wird ausreichende Beweise liefern, um zu beweisen, dass die fraglichen Dreiecke ähnlich sind.
6 Schreiben Sie den Beweis. Entwerfen Sie eine Strategie, um den Beweis zu lösen. Es gibt drei verschiedene Postulate oder mathematische Theorien, die für ähnliche Dreiecke gelten. Jeder von diesen wird ausreichende Beweise liefern, um zu beweisen, dass die fraglichen Dreiecke ähnlich sind.