Mathematische Beweise können schwierig sein, aber können mit dem richtigen Hintergrundwissen sowohl der Mathematik als auch des Formats eines Beweises überwunden werden. Leider gibt es keine schnelle und einfache Möglichkeit zu lernen, wie man einen Beweis erstellt. Sie müssen eine grundlegende Grundlage im Fach haben, um die richtigen Sätze und Definitionen zu finden, um Ihren Beweis logisch zu entwickeln. Durch das Lesen von Beispielbeweisen und das Üben allein können Sie die Fähigkeit entwickeln, einen mathematischen Beweis zu schreiben.
Methode eins von dreien:
Das Problem verstehen
-
 1 Identifizieren Sie die Frage. Sie müssen zuerst genau bestimmen, was Sie versuchen zu beweisen. Diese Frage wird auch als letzte Aussage im Beweis dienen. In diesem Schritt möchten Sie auch die Annahmen definieren, unter denen Sie arbeiten werden. Die Identifizierung der Frage und der notwendigen Annahmen gibt Ihnen einen Ausgangspunkt, um das Problem zu verstehen und den Beweis zu führen.
1 Identifizieren Sie die Frage. Sie müssen zuerst genau bestimmen, was Sie versuchen zu beweisen. Diese Frage wird auch als letzte Aussage im Beweis dienen. In diesem Schritt möchten Sie auch die Annahmen definieren, unter denen Sie arbeiten werden. Die Identifizierung der Frage und der notwendigen Annahmen gibt Ihnen einen Ausgangspunkt, um das Problem zu verstehen und den Beweis zu führen. -
 2 Zeichnen Sie Diagramme. Wenn man versucht, die innere Arbeit eines mathematischen Problems zu verstehen, ist es manchmal am einfachsten, ein Diagramm zu zeichnen, was passiert. Diagramme sind besonders wichtig in Geometry Proofs, da sie Ihnen dabei helfen zu visualisieren, was Sie tatsächlich zu beweisen versuchen.
2 Zeichnen Sie Diagramme. Wenn man versucht, die innere Arbeit eines mathematischen Problems zu verstehen, ist es manchmal am einfachsten, ein Diagramm zu zeichnen, was passiert. Diagramme sind besonders wichtig in Geometry Proofs, da sie Ihnen dabei helfen zu visualisieren, was Sie tatsächlich zu beweisen versuchen. - Verwenden Sie die Informationen in dem Problem, um eine Zeichnung des Beweises zu skizzieren. Beschriften Sie die Bekannten und Unbekannten.
- Wenn Sie den Beweis durcharbeiten, zeichnen Sie die notwendigen Informationen ein, die den Beweis liefern.
-
 3 Studiere Beweise für verwandte Sätze. Beweise sind schwer zu lernen zu schreiben, aber eine ausgezeichnete Möglichkeit, Beweise zu lernen, ist, verwandte Sätze zu studieren und wie diese bewiesen wurden.
3 Studiere Beweise für verwandte Sätze. Beweise sind schwer zu lernen zu schreiben, aber eine ausgezeichnete Möglichkeit, Beweise zu lernen, ist, verwandte Sätze zu studieren und wie diese bewiesen wurden. - Erkenne, dass ein Beweis nur ein gutes Argument ist, wenn jeder Schritt gerechtfertigt ist. Sie können viele Beweise finden, um online oder in einem Lehrbuch zu studieren.[1]
-
 4 Fragen stellen. Es ist vollkommen in Ordnung, auf einem Beweis zu bleiben. Fragen Sie Ihren Lehrer oder Mitschüler, wenn Sie Fragen haben. Sie könnten ähnliche Fragen haben und Sie können die Probleme gemeinsam bearbeiten. Es ist besser zu fragen und zu klären, als blind durch den Beweis zu stolpern.
4 Fragen stellen. Es ist vollkommen in Ordnung, auf einem Beweis zu bleiben. Fragen Sie Ihren Lehrer oder Mitschüler, wenn Sie Fragen haben. Sie könnten ähnliche Fragen haben und Sie können die Probleme gemeinsam bearbeiten. Es ist besser zu fragen und zu klären, als blind durch den Beweis zu stolpern. - Treffen Sie Ihren Lehrer außerhalb der Klasse für zusätzliche Anweisungen.
Methode zwei von drei:
Formatieren eines Beweises
-
 1 Definieren Sie mathematische Beweise. Ein mathematischer Beweis ist eine Reihe von logischen Aussagen, die von Theoremen und Definitionen gestützt werden, die die Wahrheit einer anderen mathematischen Aussage beweisen.[2] Beweise sind der einzige Weg zu wissen, dass eine Aussage mathematisch gültig ist.
1 Definieren Sie mathematische Beweise. Ein mathematischer Beweis ist eine Reihe von logischen Aussagen, die von Theoremen und Definitionen gestützt werden, die die Wahrheit einer anderen mathematischen Aussage beweisen.[2] Beweise sind der einzige Weg zu wissen, dass eine Aussage mathematisch gültig ist. - Die Fähigkeit, einen mathematischen Beweis zu schreiben, weist auf ein grundlegendes Verständnis des Problems selbst und aller in dem Problem verwendeten Konzepte hin.
- Beweise zwingen dich auch, die Mathematik auf eine neue und aufregende Weise zu betrachten. Nur indem du versuchst, etwas zu beweisen, bekommst du Wissen und Verständnis, selbst wenn dein Beweis letztendlich nicht funktioniert.
-
 2 Kenne deine Zuhörer. Bevor Sie einen Beweis schreiben, müssen Sie über die Zielgruppe nachdenken, für die Sie schreiben und welche Informationen sie bereits kennen. Wenn du einen Beweis für die Veröffentlichung schreibst, schreibst du ihn anders als einen Beweis für deine Highschool-Mathematikklasse zu schreiben.[3]
2 Kenne deine Zuhörer. Bevor Sie einen Beweis schreiben, müssen Sie über die Zielgruppe nachdenken, für die Sie schreiben und welche Informationen sie bereits kennen. Wenn du einen Beweis für die Veröffentlichung schreibst, schreibst du ihn anders als einen Beweis für deine Highschool-Mathematikklasse zu schreiben.[3] - Wenn Sie Ihre Zielgruppe kennen, können Sie den Beweis auf eine Weise schreiben, die sie angesichts der Menge an Hintergrundwissen, die sie haben, verstehen werden.
-
 3 Identifizieren Sie die Art des Beweises, den Sie schreiben. Es gibt ein paar verschiedene Arten von Beweisen, und die von Ihnen gewählte hängt von Ihrem Publikum und der Aufgabe ab. Wenn Sie nicht sicher sind, welche Version Sie verwenden sollen, fragen Sie Ihren Lehrer um Rat. In der High School wird von Ihnen erwartet, dass Sie Ihren Beweis in einem bestimmten Format verfassen, z. B. in Form eines formalen zweispaltigen Beweises.[4]
3 Identifizieren Sie die Art des Beweises, den Sie schreiben. Es gibt ein paar verschiedene Arten von Beweisen, und die von Ihnen gewählte hängt von Ihrem Publikum und der Aufgabe ab. Wenn Sie nicht sicher sind, welche Version Sie verwenden sollen, fragen Sie Ihren Lehrer um Rat. In der High School wird von Ihnen erwartet, dass Sie Ihren Beweis in einem bestimmten Format verfassen, z. B. in Form eines formalen zweispaltigen Beweises.[4] - Ein zweispaltiger Proof ist ein Setup, das in einer Spalte und in einer zweiten Spalte nebenstehende Werte und Anweisungen eingibt. Sie werden sehr häufig in der Geometrie verwendet.
- Ein informeller Absatzbeweis verwendet grammatikalisch korrekte Anweisungen und weniger Symbole. Auf höheren Ebenen sollten Sie immer einen informellen Beweis verwenden.
-
 4 Schreiben Sie den zweispaltigen Beweis als Umriss. Der zweispaltige Beweis ist eine einfache Möglichkeit, Ihre Gedanken zu ordnen und das Problem zu durchdenken. Zeichnen Sie eine Linie in der Mitte der Seite und schreiben Sie alle Angaben und Anweisungen auf der linken Seite. Schreiben Sie die entsprechenden Definitionen / Sätze auf die rechte Seite, neben den von ihnen unterstützten Gegebenheiten.
4 Schreiben Sie den zweispaltigen Beweis als Umriss. Der zweispaltige Beweis ist eine einfache Möglichkeit, Ihre Gedanken zu ordnen und das Problem zu durchdenken. Zeichnen Sie eine Linie in der Mitte der Seite und schreiben Sie alle Angaben und Anweisungen auf der linken Seite. Schreiben Sie die entsprechenden Definitionen / Sätze auf die rechte Seite, neben den von ihnen unterstützten Gegebenheiten. - Beispielsweise:[5]
- Winkel A und Winkel B bilden ein lineares Paar. Gegeben.
- Winkel ABC ist gerade. Definition eines geraden Winkels.
- Winkel ABC misst 180 °. Definition einer Linie.
- Winkel A + Winkel B = Winkel ABC. Winkeladditions-Postulat.
- Winkel A + Winkel B = 180 °. Auswechslung.
- Winkel A zusätzlich zu Winkel B. Definition von Zusatzwinkeln.
- Q.E.D.
-
 5 Konvertieren Sie den zweispaltigen Beweis in einen informellen schriftlichen Beweis. Wenn Sie den zweispaltigen Beweis als Grundlage verwenden, schreiben Sie die informelle Absatzform Ihres Beweises ohne zu viele Symbole und Abkürzungen.
5 Konvertieren Sie den zweispaltigen Beweis in einen informellen schriftlichen Beweis. Wenn Sie den zweispaltigen Beweis als Grundlage verwenden, schreiben Sie die informelle Absatzform Ihres Beweises ohne zu viele Symbole und Abkürzungen. - Zum Beispiel: Winkel A und Winkel B seien lineare Paare. Nach Hypothese sind Winkel A und Winkel B ergänzend. Winkel A und Winkel B bilden eine gerade Linie, weil sie lineare Paare sind. Eine gerade Linie ist definiert als ein Winkelmaß von 180 °. Bei gegebenem Winkeladditionspostulat summieren sich die Winkel A und B zu einer Linie ABC zusammen. Durch Substitution addieren sich die Winkel A und B zu 180 °, sie sind also ergänzende Winkel. Q.E.D.
Methode drei von drei:
Den Beweis schreiben
-
 1 Lerne das Vokabular eines Beweises. Es gibt bestimmte Aussagen und Sätze, die Sie in einem mathematischen Beweis immer wieder sehen werden. Das sind Phrasen, die Sie kennen müssen und wissen, wie Sie sie richtig benutzen, wenn Sie Ihren eigenen Beweis schreiben.[6]
1 Lerne das Vokabular eines Beweises. Es gibt bestimmte Aussagen und Sätze, die Sie in einem mathematischen Beweis immer wieder sehen werden. Das sind Phrasen, die Sie kennen müssen und wissen, wie Sie sie richtig benutzen, wenn Sie Ihren eigenen Beweis schreiben.[6] - "Wenn A, dann B" Aussagen bedeuten, dass du beweisen musst, wenn A wahr ist, muss B auch wahr sein.[7]
- "A wenn und nur wenn B" bedeutet, dass Sie beweisen müssen, dass A und B gleichzeitig wahr und falsch sind.Beweise sowohl "wenn A, dann B" und "wenn nicht A, dann nicht B".
- "A nur wenn B" ist äquivalent zu "wenn A, dann B", so wird es nicht häufig verwendet. Es ist gut, sich dessen bewusst zu sein, falls Sie es sehen.
- Vermeiden Sie bei der Erstellung des Proofs die Verwendung von "I", sondern verwenden Sie stattdessen "wir".[8]
-
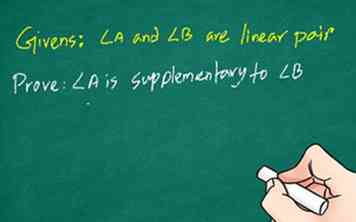 2 Schreiben Sie alle Gegebenheiten auf. Wenn ein Beweis erstellt wird, ist der erste Schritt, alle Gegebenheiten zu identifizieren und aufzuschreiben. Dies ist der beste Startpunkt, da es Ihnen hilft, zu überdenken, was bekannt ist und welche Informationen Sie benötigen, um den Beweis zu vervollständigen. Lesen Sie das Problem durch und notieren Sie jedes gegebene.
2 Schreiben Sie alle Gegebenheiten auf. Wenn ein Beweis erstellt wird, ist der erste Schritt, alle Gegebenheiten zu identifizieren und aufzuschreiben. Dies ist der beste Startpunkt, da es Ihnen hilft, zu überdenken, was bekannt ist und welche Informationen Sie benötigen, um den Beweis zu vervollständigen. Lesen Sie das Problem durch und notieren Sie jedes gegebene. - Zum Beispiel: Beweisen Sie, dass zwei Winkel (Winkel A und Winkel B), die ein lineares Paar bilden, ergänzend sind.[9]
- Givens: Winkel A und Winkel B sind ein lineares Paar
- Zeigen Sie: Winkel A ist zusätzlich zu Winkel B
-
 3 Definieren Sie alle Variablen. Neben dem Schreiben der Gegebenheiten ist es hilfreich, alle Variablen zu definieren. Schreiben Sie die Definitionen am Anfang des Beweises, um Verwirrung für den Leser zu vermeiden. Wenn Variablen nicht definiert sind, kann ein Leser leicht verloren gehen, wenn er versucht, Ihren Beweis zu verstehen.
3 Definieren Sie alle Variablen. Neben dem Schreiben der Gegebenheiten ist es hilfreich, alle Variablen zu definieren. Schreiben Sie die Definitionen am Anfang des Beweises, um Verwirrung für den Leser zu vermeiden. Wenn Variablen nicht definiert sind, kann ein Leser leicht verloren gehen, wenn er versucht, Ihren Beweis zu verstehen. - Verwenden Sie keine Variablen in Ihrem Nachweis, die nicht definiert wurden.
- Zum Beispiel: Variablen sind das Winkelmaß von Winkel A und Maß von Winkel B.
-
 4 Bearbeite den Beweis rückwärts. Es ist oft am einfachsten, das Problem rückwärts zu durchdenken. Beginnen Sie mit der Schlussfolgerung, was Sie zu beweisen versuchen, und denken Sie über die Schritte nach, die Sie an den Anfang bringen können.[10]
4 Bearbeite den Beweis rückwärts. Es ist oft am einfachsten, das Problem rückwärts zu durchdenken. Beginnen Sie mit der Schlussfolgerung, was Sie zu beweisen versuchen, und denken Sie über die Schritte nach, die Sie an den Anfang bringen können.[10] - Manipulieren Sie die Schritte vom Anfang bis zum Ende, um zu sehen, ob Sie sie wie einander aussehen lassen können. Verwenden Sie die Vorgaben, Definitionen, die Sie gelernt haben, und Beweise, die denen ähneln, an denen Sie gerade arbeiten.
- Stellen Sie sich Fragen, während Sie sich bewegen. "Warum ist das so?" und "Gibt es eine Möglichkeit, dass das falsch sein kann?" sind gute Fragen für jede Aussage oder Behauptung.
- Denken Sie daran, die Schritte in der richtigen Reihenfolge für den endgültigen Beweis neu zu schreiben.
- Zum Beispiel: Wenn Winkel A und B zusätzlich sind, müssen sie sich zu 180 ° addieren. Die beiden Winkel verbinden sich zu einer Linie ABC. Sie wissen, dass sie aufgrund der Definition linearer Paare eine Linie bilden. Da eine Linie 180 ° ist, können Sie durch Substitution beweisen, dass Winkel A und Winkel B sich zu 180 ° addieren.
-
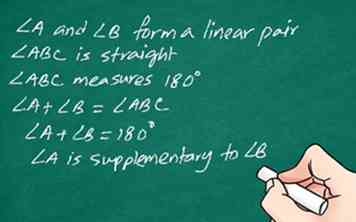 5 Bestellen Sie Ihre Schritte logisch. Beginne den Beweis zu Beginn und arbeite auf den Abschluss hin. Obwohl es hilfreich ist, über den Beweis nachzudenken, indem Sie mit dem Schluss beginnen und rückwärts arbeiten, wenn Sie den Beweis tatsächlich schreiben, geben Sie die Schlussfolgerung am Ende an.[11] Es muss von einer Anweisung zur anderen fließen, mit Unterstützung für jede Aussage, so dass es keinen Grund gibt, an der Gültigkeit Ihres Beweises zu zweifeln.
5 Bestellen Sie Ihre Schritte logisch. Beginne den Beweis zu Beginn und arbeite auf den Abschluss hin. Obwohl es hilfreich ist, über den Beweis nachzudenken, indem Sie mit dem Schluss beginnen und rückwärts arbeiten, wenn Sie den Beweis tatsächlich schreiben, geben Sie die Schlussfolgerung am Ende an.[11] Es muss von einer Anweisung zur anderen fließen, mit Unterstützung für jede Aussage, so dass es keinen Grund gibt, an der Gültigkeit Ihres Beweises zu zweifeln. - Beginnen Sie mit der Angabe der Annahmen, mit denen Sie arbeiten.
- Fügen Sie einfache und offensichtliche Schritte ein, damit sich ein Leser nicht fragen muss, wie Sie von einem Schritt zum nächsten gelangen.
- Das Schreiben mehrerer Entwürfe für Ihre Proofs ist nicht ungewöhnlich. Führen Sie eine Neuanordnung durch, bis alle Schritte in der logischsten Reihenfolge sind.
- Zum Beispiel: Beginne mit dem Anfang.
- Winkel A und Winkel B bilden ein lineares Paar.
- Winkel ABC ist gerade.
- Winkel ABC misst 180 °.
- Winkel A + Winkel B = Winkel ABC.
- Winkel A + Winkel B = Winkel 180 °.
- Winkel A ist zusätzlich zu Winkel B.
-
 6 Vermeiden Sie Pfeile und Abkürzungen im schriftlichen Beweis. Wenn Sie den Plan für Ihren Beweis skizzieren, können Sie Kurzschrift und Symbole verwenden, aber beim Schreiben des endgültigen Beweises können Symbole wie Pfeile den Leser verwirren. Verwenden Sie stattdessen Wörter wie "dann" oder "daher".[12]
6 Vermeiden Sie Pfeile und Abkürzungen im schriftlichen Beweis. Wenn Sie den Plan für Ihren Beweis skizzieren, können Sie Kurzschrift und Symbole verwenden, aber beim Schreiben des endgültigen Beweises können Symbole wie Pfeile den Leser verwirren. Verwenden Sie stattdessen Wörter wie "dann" oder "daher".[12] - Ausnahmen von der Verwendung von Abkürzungen umfassen z.B. (zum Beispiel) und d. h. (das ist), aber stellen Sie sicher, dass Sie sie richtig verwenden.[13]
-
 7 Unterstützen Sie alle Anweisungen mit einem Theorem, Gesetz oder einer Definition. Ein Beweis ist nur so gut wie die verwendeten Beweise. Sie können keine Aussage machen, ohne sie mit einer Definition zu unterstützen. Verweisen Sie auf andere Beweise, die denen ähneln, an denen Sie gerade arbeiten, zum Beispiel Beweise.
7 Unterstützen Sie alle Anweisungen mit einem Theorem, Gesetz oder einer Definition. Ein Beweis ist nur so gut wie die verwendeten Beweise. Sie können keine Aussage machen, ohne sie mit einer Definition zu unterstützen. Verweisen Sie auf andere Beweise, die denen ähneln, an denen Sie gerade arbeiten, zum Beispiel Beweise. - Versuchen Sie, Ihren Beweis auf einen Fall anzuwenden, wo es sollte Scheiternund sehen, ob es tatsächlich tut. Wenn es nicht fehlschlägt, überarbeiten Sie den Beweis, so dass es funktioniert.
- Viele geometrische Beweise werden als zweispaltiger Beweis mit der Aussage und dem Beweis geschrieben. Ein formaler mathematischer Beweis für die Veröffentlichung wird als ein Absatz mit korrekter Grammatik geschrieben.
-
 8 Schluss mit einer Schlussfolgerung oder Q.E.D. Die letzte Aussage des Beweises sollte das Konzept sein, das Sie beweisen wollten. Sobald Sie diese Aussage gemacht haben, beenden Sie den Beweis mit einem abschließenden Schlusszeichen wie Q.E.D. oder ein ausgefülltes Quadrat zeigt an, dass der Proof vollständig abgeschlossen ist.[14]
8 Schluss mit einer Schlussfolgerung oder Q.E.D. Die letzte Aussage des Beweises sollte das Konzept sein, das Sie beweisen wollten. Sobald Sie diese Aussage gemacht haben, beenden Sie den Beweis mit einem abschließenden Schlusszeichen wie Q.E.D. oder ein ausgefülltes Quadrat zeigt an, dass der Proof vollständig abgeschlossen ist.[14] - Q.E.D. (quod erat demonstrandum, lateinisch für "was gezeigt werden sollte").
- Wenn du dir nicht sicher bist, ob dein Beweis korrekt ist, schreibe einfach ein paar Sätze, die sagen, was deine Schlussfolgerung war und warum sie signifikant ist.
 Minotauromaquia
Minotauromaquia
 1 Identifizieren Sie die Frage. Sie müssen zuerst genau bestimmen, was Sie versuchen zu beweisen. Diese Frage wird auch als letzte Aussage im Beweis dienen. In diesem Schritt möchten Sie auch die Annahmen definieren, unter denen Sie arbeiten werden. Die Identifizierung der Frage und der notwendigen Annahmen gibt Ihnen einen Ausgangspunkt, um das Problem zu verstehen und den Beweis zu führen.
1 Identifizieren Sie die Frage. Sie müssen zuerst genau bestimmen, was Sie versuchen zu beweisen. Diese Frage wird auch als letzte Aussage im Beweis dienen. In diesem Schritt möchten Sie auch die Annahmen definieren, unter denen Sie arbeiten werden. Die Identifizierung der Frage und der notwendigen Annahmen gibt Ihnen einen Ausgangspunkt, um das Problem zu verstehen und den Beweis zu führen.  2 Zeichnen Sie Diagramme. Wenn man versucht, die innere Arbeit eines mathematischen Problems zu verstehen, ist es manchmal am einfachsten, ein Diagramm zu zeichnen, was passiert. Diagramme sind besonders wichtig in Geometry Proofs, da sie Ihnen dabei helfen zu visualisieren, was Sie tatsächlich zu beweisen versuchen.
2 Zeichnen Sie Diagramme. Wenn man versucht, die innere Arbeit eines mathematischen Problems zu verstehen, ist es manchmal am einfachsten, ein Diagramm zu zeichnen, was passiert. Diagramme sind besonders wichtig in Geometry Proofs, da sie Ihnen dabei helfen zu visualisieren, was Sie tatsächlich zu beweisen versuchen.  3 Studiere Beweise für verwandte Sätze. Beweise sind schwer zu lernen zu schreiben, aber eine ausgezeichnete Möglichkeit, Beweise zu lernen, ist, verwandte Sätze zu studieren und wie diese bewiesen wurden.
3 Studiere Beweise für verwandte Sätze. Beweise sind schwer zu lernen zu schreiben, aber eine ausgezeichnete Möglichkeit, Beweise zu lernen, ist, verwandte Sätze zu studieren und wie diese bewiesen wurden.  4 Fragen stellen. Es ist vollkommen in Ordnung, auf einem Beweis zu bleiben. Fragen Sie Ihren Lehrer oder Mitschüler, wenn Sie Fragen haben. Sie könnten ähnliche Fragen haben und Sie können die Probleme gemeinsam bearbeiten. Es ist besser zu fragen und zu klären, als blind durch den Beweis zu stolpern.
4 Fragen stellen. Es ist vollkommen in Ordnung, auf einem Beweis zu bleiben. Fragen Sie Ihren Lehrer oder Mitschüler, wenn Sie Fragen haben. Sie könnten ähnliche Fragen haben und Sie können die Probleme gemeinsam bearbeiten. Es ist besser zu fragen und zu klären, als blind durch den Beweis zu stolpern.  1 Definieren Sie mathematische Beweise. Ein mathematischer Beweis ist eine Reihe von logischen Aussagen, die von Theoremen und Definitionen gestützt werden, die die Wahrheit einer anderen mathematischen Aussage beweisen.[2] Beweise sind der einzige Weg zu wissen, dass eine Aussage mathematisch gültig ist.
1 Definieren Sie mathematische Beweise. Ein mathematischer Beweis ist eine Reihe von logischen Aussagen, die von Theoremen und Definitionen gestützt werden, die die Wahrheit einer anderen mathematischen Aussage beweisen.[2] Beweise sind der einzige Weg zu wissen, dass eine Aussage mathematisch gültig ist.  2 Kenne deine Zuhörer. Bevor Sie einen Beweis schreiben, müssen Sie über die Zielgruppe nachdenken, für die Sie schreiben und welche Informationen sie bereits kennen. Wenn du einen Beweis für die Veröffentlichung schreibst, schreibst du ihn anders als einen Beweis für deine Highschool-Mathematikklasse zu schreiben.[3]
2 Kenne deine Zuhörer. Bevor Sie einen Beweis schreiben, müssen Sie über die Zielgruppe nachdenken, für die Sie schreiben und welche Informationen sie bereits kennen. Wenn du einen Beweis für die Veröffentlichung schreibst, schreibst du ihn anders als einen Beweis für deine Highschool-Mathematikklasse zu schreiben.[3]  3 Identifizieren Sie die Art des Beweises, den Sie schreiben. Es gibt ein paar verschiedene Arten von Beweisen, und die von Ihnen gewählte hängt von Ihrem Publikum und der Aufgabe ab. Wenn Sie nicht sicher sind, welche Version Sie verwenden sollen, fragen Sie Ihren Lehrer um Rat. In der High School wird von Ihnen erwartet, dass Sie Ihren Beweis in einem bestimmten Format verfassen, z. B. in Form eines formalen zweispaltigen Beweises.[4]
3 Identifizieren Sie die Art des Beweises, den Sie schreiben. Es gibt ein paar verschiedene Arten von Beweisen, und die von Ihnen gewählte hängt von Ihrem Publikum und der Aufgabe ab. Wenn Sie nicht sicher sind, welche Version Sie verwenden sollen, fragen Sie Ihren Lehrer um Rat. In der High School wird von Ihnen erwartet, dass Sie Ihren Beweis in einem bestimmten Format verfassen, z. B. in Form eines formalen zweispaltigen Beweises.[4]  4 Schreiben Sie den zweispaltigen Beweis als Umriss. Der zweispaltige Beweis ist eine einfache Möglichkeit, Ihre Gedanken zu ordnen und das Problem zu durchdenken. Zeichnen Sie eine Linie in der Mitte der Seite und schreiben Sie alle Angaben und Anweisungen auf der linken Seite. Schreiben Sie die entsprechenden Definitionen / Sätze auf die rechte Seite, neben den von ihnen unterstützten Gegebenheiten.
4 Schreiben Sie den zweispaltigen Beweis als Umriss. Der zweispaltige Beweis ist eine einfache Möglichkeit, Ihre Gedanken zu ordnen und das Problem zu durchdenken. Zeichnen Sie eine Linie in der Mitte der Seite und schreiben Sie alle Angaben und Anweisungen auf der linken Seite. Schreiben Sie die entsprechenden Definitionen / Sätze auf die rechte Seite, neben den von ihnen unterstützten Gegebenheiten.  5 Konvertieren Sie den zweispaltigen Beweis in einen informellen schriftlichen Beweis. Wenn Sie den zweispaltigen Beweis als Grundlage verwenden, schreiben Sie die informelle Absatzform Ihres Beweises ohne zu viele Symbole und Abkürzungen.
5 Konvertieren Sie den zweispaltigen Beweis in einen informellen schriftlichen Beweis. Wenn Sie den zweispaltigen Beweis als Grundlage verwenden, schreiben Sie die informelle Absatzform Ihres Beweises ohne zu viele Symbole und Abkürzungen.  1 Lerne das Vokabular eines Beweises. Es gibt bestimmte Aussagen und Sätze, die Sie in einem mathematischen Beweis immer wieder sehen werden. Das sind Phrasen, die Sie kennen müssen und wissen, wie Sie sie richtig benutzen, wenn Sie Ihren eigenen Beweis schreiben.[6]
1 Lerne das Vokabular eines Beweises. Es gibt bestimmte Aussagen und Sätze, die Sie in einem mathematischen Beweis immer wieder sehen werden. Das sind Phrasen, die Sie kennen müssen und wissen, wie Sie sie richtig benutzen, wenn Sie Ihren eigenen Beweis schreiben.[6] 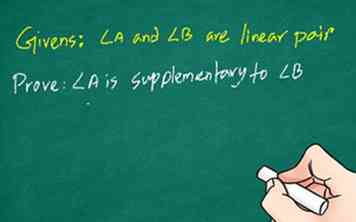 2 Schreiben Sie alle Gegebenheiten auf. Wenn ein Beweis erstellt wird, ist der erste Schritt, alle Gegebenheiten zu identifizieren und aufzuschreiben. Dies ist der beste Startpunkt, da es Ihnen hilft, zu überdenken, was bekannt ist und welche Informationen Sie benötigen, um den Beweis zu vervollständigen. Lesen Sie das Problem durch und notieren Sie jedes gegebene.
2 Schreiben Sie alle Gegebenheiten auf. Wenn ein Beweis erstellt wird, ist der erste Schritt, alle Gegebenheiten zu identifizieren und aufzuschreiben. Dies ist der beste Startpunkt, da es Ihnen hilft, zu überdenken, was bekannt ist und welche Informationen Sie benötigen, um den Beweis zu vervollständigen. Lesen Sie das Problem durch und notieren Sie jedes gegebene.  3 Definieren Sie alle Variablen. Neben dem Schreiben der Gegebenheiten ist es hilfreich, alle Variablen zu definieren. Schreiben Sie die Definitionen am Anfang des Beweises, um Verwirrung für den Leser zu vermeiden. Wenn Variablen nicht definiert sind, kann ein Leser leicht verloren gehen, wenn er versucht, Ihren Beweis zu verstehen.
3 Definieren Sie alle Variablen. Neben dem Schreiben der Gegebenheiten ist es hilfreich, alle Variablen zu definieren. Schreiben Sie die Definitionen am Anfang des Beweises, um Verwirrung für den Leser zu vermeiden. Wenn Variablen nicht definiert sind, kann ein Leser leicht verloren gehen, wenn er versucht, Ihren Beweis zu verstehen.  4 Bearbeite den Beweis rückwärts. Es ist oft am einfachsten, das Problem rückwärts zu durchdenken. Beginnen Sie mit der Schlussfolgerung, was Sie zu beweisen versuchen, und denken Sie über die Schritte nach, die Sie an den Anfang bringen können.[10]
4 Bearbeite den Beweis rückwärts. Es ist oft am einfachsten, das Problem rückwärts zu durchdenken. Beginnen Sie mit der Schlussfolgerung, was Sie zu beweisen versuchen, und denken Sie über die Schritte nach, die Sie an den Anfang bringen können.[10] 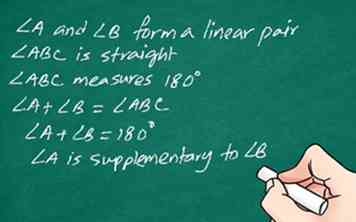 5 Bestellen Sie Ihre Schritte logisch. Beginne den Beweis zu Beginn und arbeite auf den Abschluss hin. Obwohl es hilfreich ist, über den Beweis nachzudenken, indem Sie mit dem Schluss beginnen und rückwärts arbeiten, wenn Sie den Beweis tatsächlich schreiben, geben Sie die Schlussfolgerung am Ende an.[11] Es muss von einer Anweisung zur anderen fließen, mit Unterstützung für jede Aussage, so dass es keinen Grund gibt, an der Gültigkeit Ihres Beweises zu zweifeln.
5 Bestellen Sie Ihre Schritte logisch. Beginne den Beweis zu Beginn und arbeite auf den Abschluss hin. Obwohl es hilfreich ist, über den Beweis nachzudenken, indem Sie mit dem Schluss beginnen und rückwärts arbeiten, wenn Sie den Beweis tatsächlich schreiben, geben Sie die Schlussfolgerung am Ende an.[11] Es muss von einer Anweisung zur anderen fließen, mit Unterstützung für jede Aussage, so dass es keinen Grund gibt, an der Gültigkeit Ihres Beweises zu zweifeln.  6 Vermeiden Sie Pfeile und Abkürzungen im schriftlichen Beweis. Wenn Sie den Plan für Ihren Beweis skizzieren, können Sie Kurzschrift und Symbole verwenden, aber beim Schreiben des endgültigen Beweises können Symbole wie Pfeile den Leser verwirren. Verwenden Sie stattdessen Wörter wie "dann" oder "daher".[12]
6 Vermeiden Sie Pfeile und Abkürzungen im schriftlichen Beweis. Wenn Sie den Plan für Ihren Beweis skizzieren, können Sie Kurzschrift und Symbole verwenden, aber beim Schreiben des endgültigen Beweises können Symbole wie Pfeile den Leser verwirren. Verwenden Sie stattdessen Wörter wie "dann" oder "daher".[12]  7 Unterstützen Sie alle Anweisungen mit einem Theorem, Gesetz oder einer Definition. Ein Beweis ist nur so gut wie die verwendeten Beweise. Sie können keine Aussage machen, ohne sie mit einer Definition zu unterstützen. Verweisen Sie auf andere Beweise, die denen ähneln, an denen Sie gerade arbeiten, zum Beispiel Beweise.
7 Unterstützen Sie alle Anweisungen mit einem Theorem, Gesetz oder einer Definition. Ein Beweis ist nur so gut wie die verwendeten Beweise. Sie können keine Aussage machen, ohne sie mit einer Definition zu unterstützen. Verweisen Sie auf andere Beweise, die denen ähneln, an denen Sie gerade arbeiten, zum Beispiel Beweise.  8 Schluss mit einer Schlussfolgerung oder Q.E.D. Die letzte Aussage des Beweises sollte das Konzept sein, das Sie beweisen wollten. Sobald Sie diese Aussage gemacht haben, beenden Sie den Beweis mit einem abschließenden Schlusszeichen wie Q.E.D. oder ein ausgefülltes Quadrat zeigt an, dass der Proof vollständig abgeschlossen ist.[14]
8 Schluss mit einer Schlussfolgerung oder Q.E.D. Die letzte Aussage des Beweises sollte das Konzept sein, das Sie beweisen wollten. Sobald Sie diese Aussage gemacht haben, beenden Sie den Beweis mit einem abschließenden Schlusszeichen wie Q.E.D. oder ein ausgefülltes Quadrat zeigt an, dass der Proof vollständig abgeschlossen ist.[14]