Der y-Achsenabschnitt einer Gleichung ist ein Punkt, an dem der Graph der Gleichung die Y-Achse schneidet. Es gibt mehrere Möglichkeiten, den y-Achsenabschnitt einer Gleichung zu finden, abhängig von den Anfangsinformationen, die Sie haben.
Methode eins von dreien:
Finden des Y-Intercept von der Steigung und dem Punkt
-
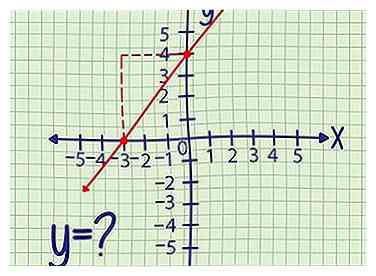 1 Schreiben Sie die Steigung und den Punkt auf. Die Steigung oder "rise over run" ist eine einzelne Zahl, die angibt, wie steil die Linie ist. Diese Art von Problem gibt Ihnen auch die (x, y) Koordinate eines Punktes entlang des Graphen. Gehen Sie zu den folgenden Methoden, wenn Sie diese beiden Informationen nicht haben.
1 Schreiben Sie die Steigung und den Punkt auf. Die Steigung oder "rise over run" ist eine einzelne Zahl, die angibt, wie steil die Linie ist. Diese Art von Problem gibt Ihnen auch die (x, y) Koordinate eines Punktes entlang des Graphen. Gehen Sie zu den folgenden Methoden, wenn Sie diese beiden Informationen nicht haben. - Beispiel 1: Eine gerade Linie mit Steigung 2 enthält den Punkt (-3,4). Finden Sie den y-Achsenabschnitt dieser Linie mit den folgenden Schritten.
-
 2 Erlernen Sie die Steigung-abfangen Form einer Gleichung. Jede gerade Linie kann als eine Gleichung in das Formular geschrieben werden y = mx + b. Wenn die Gleichung in dieser Form ist, die Variable m ist die Steigung und b ist der y-Achsenabschnitt.
2 Erlernen Sie die Steigung-abfangen Form einer Gleichung. Jede gerade Linie kann als eine Gleichung in das Formular geschrieben werden y = mx + b. Wenn die Gleichung in dieser Form ist, die Variable m ist die Steigung und b ist der y-Achsenabschnitt. -
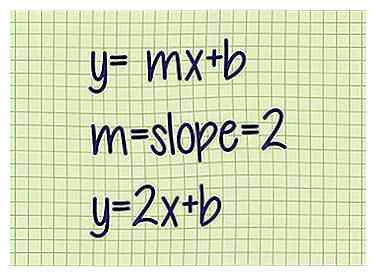 3 Ersetzen Sie die Steigung in dieser Gleichung. Schreiben Sie die Steigung-Schnittpunkt-Gleichung, aber statt mBenutze die Steigung deiner Linie.
3 Ersetzen Sie die Steigung in dieser Gleichung. Schreiben Sie die Steigung-Schnittpunkt-Gleichung, aber statt mBenutze die Steigung deiner Linie. - Beispiel 1 (Fortsetzung): y = mx + b
m = Steigung = 2
y = 2x + b
- Beispiel 1 (Fortsetzung): y = mx + b
-
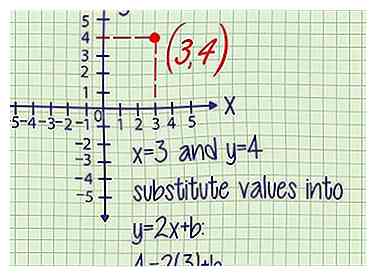 4 Ersetzen Sie x und y durch die Koordinaten des Punktes. Jedes Mal, wenn Sie die Koordinaten eines einzelnen Punktes in Ihrer Linie haben, können Sie diese ersetzen x und y Koordinaten für die x und y in deiner Liniengleichung. Tun Sie dies für die Gleichung, an der Sie gearbeitet haben.
4 Ersetzen Sie x und y durch die Koordinaten des Punktes. Jedes Mal, wenn Sie die Koordinaten eines einzelnen Punktes in Ihrer Linie haben, können Sie diese ersetzen x und y Koordinaten für die x und y in deiner Liniengleichung. Tun Sie dies für die Gleichung, an der Sie gearbeitet haben. - Beispiel 1 (Fortsetzung): Der Punkt (3,4) befindet sich auf dieser Linie. An diesem Punkt, x = 3 und y = 4.
Ersetzen Sie diese Werte in y = 2x + b:
4 = 2(3) + b
- Beispiel 1 (Fortsetzung): Der Punkt (3,4) befindet sich auf dieser Linie. An diesem Punkt, x = 3 und y = 4.
-
 5 Lösen für b. Merken, b ist der y-Schnittpunkt der Linie. Nun das b ist die einzige Variable in der Gleichung, neu anordnen, um für diese Variable zu lösen und die Antwort zu finden.
5 Lösen für b. Merken, b ist der y-Schnittpunkt der Linie. Nun das b ist die einzige Variable in der Gleichung, neu anordnen, um für diese Variable zu lösen und die Antwort zu finden. - Beispiel 1 (Fortsetzung): 4 = 2 (3) + b
4 = 6 + b
4 - 6 = b
-2 = b
Der y-Achsenabschnitt dieser Linie ist -2.
- Beispiel 1 (Fortsetzung): 4 = 2 (3) + b
-
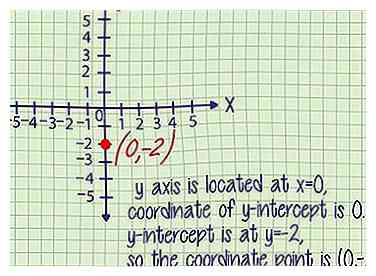 6 Schreiben Sie dies als Koordinatenpunkt. Der y-Schnittpunkt ist der Schnittpunkt der Linie mit der y-Achse. Da die y-Achse bei x = 0 liegt, ist die x-Koordinate des y-Achsenabschnitts immer 0.
6 Schreiben Sie dies als Koordinatenpunkt. Der y-Schnittpunkt ist der Schnittpunkt der Linie mit der y-Achse. Da die y-Achse bei x = 0 liegt, ist die x-Koordinate des y-Achsenabschnitts immer 0. - Beispiel 1 (Fortsetzung): Der y-Achsenabschnitt liegt bei y = -2, der Koordinatenpunkt ist also (0, -2).
Methode zwei von drei:
Mit zwei Punkten
-
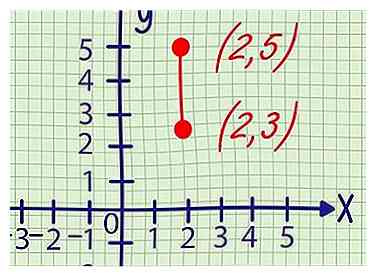 1 Schreiben Sie die Koordinaten beider Punkte auf. Diese Methode behandelt Probleme, bei denen nur zwei Punkte auf einer geraden Linie angezeigt werden. Schreiben Sie jede Punktkoordinate in (x, y) -Form nieder.
1 Schreiben Sie die Koordinaten beider Punkte auf. Diese Methode behandelt Probleme, bei denen nur zwei Punkte auf einer geraden Linie angezeigt werden. Schreiben Sie jede Punktkoordinate in (x, y) -Form nieder. -
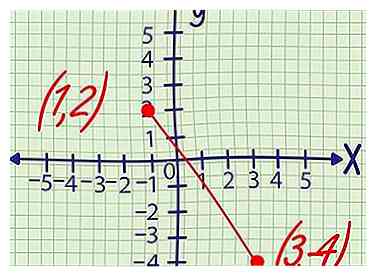 2 Beispiel 2: Eine gerade Linie verläuft durch Punkte (1, 2) und (3, -4). Finden Sie den y-Achsenabschnitt dieser Linie mit den folgenden Schritten.
2 Beispiel 2: Eine gerade Linie verläuft durch Punkte (1, 2) und (3, -4). Finden Sie den y-Achsenabschnitt dieser Linie mit den folgenden Schritten. -
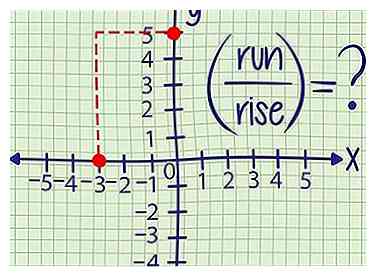 3 Berechnen Sie den Anstieg und den Lauf. Die Steigung ist ein Maß dafür, um wie viel vertikale Entfernung sich die Linie für jede horizontale Einheit bewegt. Sie haben das vielleicht als "Rise over run" (). So finden Sie diese zwei Größen von zwei Punkten:
3 Berechnen Sie den Anstieg und den Lauf. Die Steigung ist ein Maß dafür, um wie viel vertikale Entfernung sich die Linie für jede horizontale Einheit bewegt. Sie haben das vielleicht als "Rise over run" (). So finden Sie diese zwei Größen von zwei Punkten: - "Rise" ist die Änderung der vertikalen Distanz oder der Unterschied zwischen der y-Werte der zwei Punkte.
- "Run" ist die Änderung der horizontalen Distanz oder der Unterschied zwischen x-Werte der gleichen zwei Punkte.
- Beispiel 2 (Fortsetzung): Die y-Werte der beiden Punkte sind 2 und -4, also ist der Anstieg (-4) - (2) = -6.
Die x-Werte der zwei Punkte (in der gleichen Reihenfolge) sind 1 und 3, also ist der Lauf 3 - 1 = 2.
-
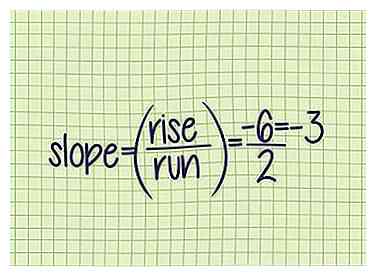 4 Teilt den Lauf, um den Hang zu finden. Nun, da Sie diese zwei Werte kennen, stecken Sie sie in ""um die Steigung der Linie zu finden.
4 Teilt den Lauf, um den Hang zu finden. Nun, da Sie diese zwei Werte kennen, stecken Sie sie in ""um die Steigung der Linie zu finden. - Beispiel 2 (Fortsetzung): -3.
-
 5 Überprüfen Sie die Form des Pistenabschnitts. Sie können eine Gerade mit der Formel beschreiben y = mx + b, woher m ist die Steigung und b ist der y-Achsenabschnitt. Jetzt wissen wir die Steigung m und einen Punkt (x, y) können wir mit dieser Gleichung lösen b, der y-Schnittpunkt.
5 Überprüfen Sie die Form des Pistenabschnitts. Sie können eine Gerade mit der Formel beschreiben y = mx + b, woher m ist die Steigung und b ist der y-Achsenabschnitt. Jetzt wissen wir die Steigung m und einen Punkt (x, y) können wir mit dieser Gleichung lösen b, der y-Schnittpunkt. -
 6 Passen Sie die Steigung und den Punkt in die Gleichung ein. Nimm die Gleichung in der Form des Steigungsabfangs und ersetze sie m mit der Steigung, die du berechnet hast. Ersetze das x und y Begriffe mit den Koordinaten eines einzelnen Punktes auf der Linie. Es spielt keine Rolle, welchen Punkt Sie verwenden.
6 Passen Sie die Steigung und den Punkt in die Gleichung ein. Nimm die Gleichung in der Form des Steigungsabfangs und ersetze sie m mit der Steigung, die du berechnet hast. Ersetze das x und y Begriffe mit den Koordinaten eines einzelnen Punktes auf der Linie. Es spielt keine Rolle, welchen Punkt Sie verwenden. - Beispiel 2 (Fortsetzung): y = mx + b
Steigung = m = -3, so y = -3x + b
Die Linie enthält einen Punkt mit (x, y) Koordinaten (1,2), also 2 = -3 (1) + b.
- Beispiel 2 (Fortsetzung): y = mx + b
-
 7 Lösung für b. Jetzt ist die einzige Variable in der Gleichung übrig b, der y-Schnittpunkt. Ordne die Gleichung so um b ist auf der einen Seite, und Sie haben Ihre Antwort. Denken Sie daran, dass der y-Schnittpunkt immer eine x-Koordinate von 0 hat.
7 Lösung für b. Jetzt ist die einzige Variable in der Gleichung übrig b, der y-Schnittpunkt. Ordne die Gleichung so um b ist auf der einen Seite, und Sie haben Ihre Antwort. Denken Sie daran, dass der y-Schnittpunkt immer eine x-Koordinate von 0 hat. - Beispiel 2 (Fortsetzung): 2 = -3 (1) + b
2 = -3 + b
5 = b
Der y-Achsenabschnitt ist bei (0,5).
- Beispiel 2 (Fortsetzung): 2 = -3 (1) + b
Methode drei von drei:
Eine Gleichung verwenden
-
 1 Schreiben Sie die Gleichung der Linie auf. Wenn Sie bereits die Gleichung der Linie haben, können Sie den y-Abschnitt mit einer kleinen Algebra finden.
1 Schreiben Sie die Gleichung der Linie auf. Wenn Sie bereits die Gleichung der Linie haben, können Sie den y-Abschnitt mit einer kleinen Algebra finden. - Beispiel 3: Was ist der y-Schnittpunkt der Linie? x + 4y = 16?
- Hinweis: Beispiel 3 ist eine gerade Linie. Am Ende dieses Abschnitts finden Sie ein Beispiel für eine quadratische Gleichung (mit einer Potenz von 2).
-
 2 Stellvertreter 0 für x. Die y-Achse ist eine vertikale Linie entlang x = 0. Dies bedeutet, dass jeder Punkt auf der y-Achse eine x-Koordinate von 0 hat, einschließlich des y-Schnittpunkts der Linie.Stecken Sie 0 für x in die Liniengleichung ein.
2 Stellvertreter 0 für x. Die y-Achse ist eine vertikale Linie entlang x = 0. Dies bedeutet, dass jeder Punkt auf der y-Achse eine x-Koordinate von 0 hat, einschließlich des y-Schnittpunkts der Linie.Stecken Sie 0 für x in die Liniengleichung ein. - Beispiel 3 (Forts.): x + 4y = 16
x = 0
0 + 4y = 16
4y = 16
- Beispiel 3 (Forts.): x + 4y = 16
-
 3 Löse für y. Die Antwort ist der y-Schnittpunkt der Linie.
3 Löse für y. Die Antwort ist der y-Schnittpunkt der Linie. - Beispiel 3 (Forts.): 4y = 16
y = 4.
Der y-Achsenabschnitt der Linie ist 4.
- Beispiel 3 (Forts.): 4y = 16
-
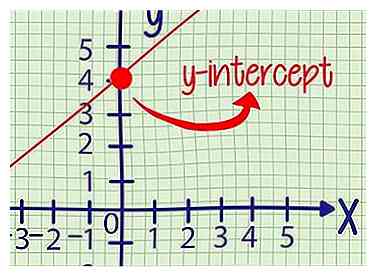 4 Bestätigen Sie mit der grafischen Darstellung (optional). Um Ihre Antwort zu überprüfen, zeichnen Sie die Gleichung so gut wie möglich auf. Der Punkt, an dem die Linie die y-Achse kreuzt, ist der y-Achsenabschnitt.
4 Bestätigen Sie mit der grafischen Darstellung (optional). Um Ihre Antwort zu überprüfen, zeichnen Sie die Gleichung so gut wie möglich auf. Der Punkt, an dem die Linie die y-Achse kreuzt, ist der y-Achsenabschnitt. -
 5 Finde den y-Achsenabschnitt für eine quadratische Gleichung. Eine quadratische Gleichung enthält eine Variable (x oder y), die auf die Potenz von 2 erhöht wird. Sie können mit derselben Substitution nach y auflösen, aber da die Quadra- te eine Kurve beschreibt, könnte sie die y-Achse bei 0, 1 oder 2 abfangen Punkte. Das bedeutet, dass Sie mit 0, 1 oder 2 Antworten enden können.
5 Finde den y-Achsenabschnitt für eine quadratische Gleichung. Eine quadratische Gleichung enthält eine Variable (x oder y), die auf die Potenz von 2 erhöht wird. Sie können mit derselben Substitution nach y auflösen, aber da die Quadra- te eine Kurve beschreibt, könnte sie die y-Achse bei 0, 1 oder 2 abfangen Punkte. Das bedeutet, dass Sie mit 0, 1 oder 2 Antworten enden können. - Beispiel 4: Um den y-Achsenabschnitt von zu finden , ersetze x = 0 und löse die quadratische Gleichung.
In diesem Fall können wir lösen indem Sie die Quadratwurzel von beiden Seiten nehmen. Denken Sie daran, wenn Sie eine Quadratwurzel nehmen, müssen Sie zwei Antworten berücksichtigen: eine negative und eine positive.
y = 1 oder y = -1. Dies sind beide y-Abschnitte dieser Kurve.
- Beispiel 4: Um den y-Achsenabschnitt von zu finden , ersetze x = 0 und löse die quadratische Gleichung.
 Minotauromaquia
Minotauromaquia
 1 Schreiben Sie die Steigung und den Punkt auf. Die Steigung oder "rise over run" ist eine einzelne Zahl, die angibt, wie steil die Linie ist. Diese Art von Problem gibt Ihnen auch die (x, y) Koordinate eines Punktes entlang des Graphen. Gehen Sie zu den folgenden Methoden, wenn Sie diese beiden Informationen nicht haben.
1 Schreiben Sie die Steigung und den Punkt auf. Die Steigung oder "rise over run" ist eine einzelne Zahl, die angibt, wie steil die Linie ist. Diese Art von Problem gibt Ihnen auch die (x, y) Koordinate eines Punktes entlang des Graphen. Gehen Sie zu den folgenden Methoden, wenn Sie diese beiden Informationen nicht haben.  2 Erlernen Sie die Steigung-abfangen Form einer Gleichung. Jede gerade Linie kann als eine Gleichung in das Formular geschrieben werden y = mx + b. Wenn die Gleichung in dieser Form ist, die Variable m ist die Steigung und b ist der y-Achsenabschnitt.
2 Erlernen Sie die Steigung-abfangen Form einer Gleichung. Jede gerade Linie kann als eine Gleichung in das Formular geschrieben werden y = mx + b. Wenn die Gleichung in dieser Form ist, die Variable m ist die Steigung und b ist der y-Achsenabschnitt. 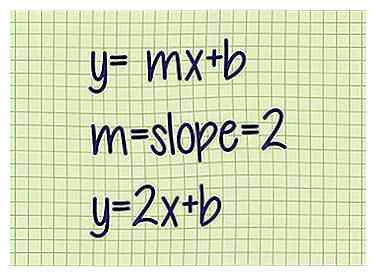 3 Ersetzen Sie die Steigung in dieser Gleichung. Schreiben Sie die Steigung-Schnittpunkt-Gleichung, aber statt mBenutze die Steigung deiner Linie.
3 Ersetzen Sie die Steigung in dieser Gleichung. Schreiben Sie die Steigung-Schnittpunkt-Gleichung, aber statt mBenutze die Steigung deiner Linie. 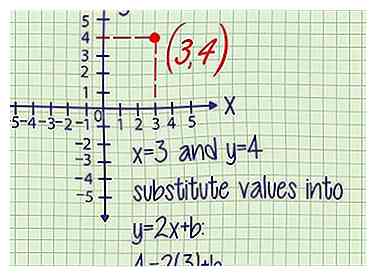 4 Ersetzen Sie x und y durch die Koordinaten des Punktes. Jedes Mal, wenn Sie die Koordinaten eines einzelnen Punktes in Ihrer Linie haben, können Sie diese ersetzen x und y Koordinaten für die x und y in deiner Liniengleichung. Tun Sie dies für die Gleichung, an der Sie gearbeitet haben.
4 Ersetzen Sie x und y durch die Koordinaten des Punktes. Jedes Mal, wenn Sie die Koordinaten eines einzelnen Punktes in Ihrer Linie haben, können Sie diese ersetzen x und y Koordinaten für die x und y in deiner Liniengleichung. Tun Sie dies für die Gleichung, an der Sie gearbeitet haben.  5 Lösen für b. Merken, b ist der y-Schnittpunkt der Linie. Nun das b ist die einzige Variable in der Gleichung, neu anordnen, um für diese Variable zu lösen und die Antwort zu finden.
5 Lösen für b. Merken, b ist der y-Schnittpunkt der Linie. Nun das b ist die einzige Variable in der Gleichung, neu anordnen, um für diese Variable zu lösen und die Antwort zu finden.  6 Schreiben Sie dies als Koordinatenpunkt. Der y-Schnittpunkt ist der Schnittpunkt der Linie mit der y-Achse. Da die y-Achse bei x = 0 liegt, ist die x-Koordinate des y-Achsenabschnitts immer 0.
6 Schreiben Sie dies als Koordinatenpunkt. Der y-Schnittpunkt ist der Schnittpunkt der Linie mit der y-Achse. Da die y-Achse bei x = 0 liegt, ist die x-Koordinate des y-Achsenabschnitts immer 0.  1 Schreiben Sie die Koordinaten beider Punkte auf. Diese Methode behandelt Probleme, bei denen nur zwei Punkte auf einer geraden Linie angezeigt werden. Schreiben Sie jede Punktkoordinate in (x, y) -Form nieder.
1 Schreiben Sie die Koordinaten beider Punkte auf. Diese Methode behandelt Probleme, bei denen nur zwei Punkte auf einer geraden Linie angezeigt werden. Schreiben Sie jede Punktkoordinate in (x, y) -Form nieder.  2 Beispiel 2: Eine gerade Linie verläuft durch Punkte (1, 2) und (3, -4). Finden Sie den y-Achsenabschnitt dieser Linie mit den folgenden Schritten.
2 Beispiel 2: Eine gerade Linie verläuft durch Punkte (1, 2) und (3, -4). Finden Sie den y-Achsenabschnitt dieser Linie mit den folgenden Schritten.  3 Berechnen Sie den Anstieg und den Lauf. Die Steigung ist ein Maß dafür, um wie viel vertikale Entfernung sich die Linie für jede horizontale Einheit bewegt. Sie haben das vielleicht als "Rise over run" (
3 Berechnen Sie den Anstieg und den Lauf. Die Steigung ist ein Maß dafür, um wie viel vertikale Entfernung sich die Linie für jede horizontale Einheit bewegt. Sie haben das vielleicht als "Rise over run" (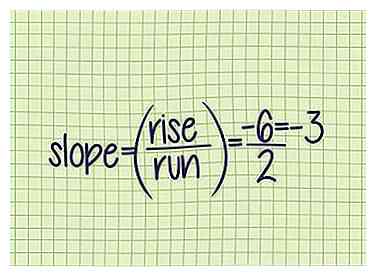 4 Teilt den Lauf, um den Hang zu finden. Nun, da Sie diese zwei Werte kennen, stecken Sie sie in "
4 Teilt den Lauf, um den Hang zu finden. Nun, da Sie diese zwei Werte kennen, stecken Sie sie in " 5 Überprüfen Sie die Form des Pistenabschnitts. Sie können eine Gerade mit der Formel beschreiben y = mx + b, woher m ist die Steigung und b ist der y-Achsenabschnitt. Jetzt wissen wir die Steigung m und einen Punkt (x, y) können wir mit dieser Gleichung lösen b, der y-Schnittpunkt.
5 Überprüfen Sie die Form des Pistenabschnitts. Sie können eine Gerade mit der Formel beschreiben y = mx + b, woher m ist die Steigung und b ist der y-Achsenabschnitt. Jetzt wissen wir die Steigung m und einen Punkt (x, y) können wir mit dieser Gleichung lösen b, der y-Schnittpunkt.  6 Passen Sie die Steigung und den Punkt in die Gleichung ein. Nimm die Gleichung in der Form des Steigungsabfangs und ersetze sie m mit der Steigung, die du berechnet hast. Ersetze das x und y Begriffe mit den Koordinaten eines einzelnen Punktes auf der Linie. Es spielt keine Rolle, welchen Punkt Sie verwenden.
6 Passen Sie die Steigung und den Punkt in die Gleichung ein. Nimm die Gleichung in der Form des Steigungsabfangs und ersetze sie m mit der Steigung, die du berechnet hast. Ersetze das x und y Begriffe mit den Koordinaten eines einzelnen Punktes auf der Linie. Es spielt keine Rolle, welchen Punkt Sie verwenden.  7 Lösung für b. Jetzt ist die einzige Variable in der Gleichung übrig b, der y-Schnittpunkt. Ordne die Gleichung so um b ist auf der einen Seite, und Sie haben Ihre Antwort. Denken Sie daran, dass der y-Schnittpunkt immer eine x-Koordinate von 0 hat.
7 Lösung für b. Jetzt ist die einzige Variable in der Gleichung übrig b, der y-Schnittpunkt. Ordne die Gleichung so um b ist auf der einen Seite, und Sie haben Ihre Antwort. Denken Sie daran, dass der y-Schnittpunkt immer eine x-Koordinate von 0 hat.  1 Schreiben Sie die Gleichung der Linie auf. Wenn Sie bereits die Gleichung der Linie haben, können Sie den y-Abschnitt mit einer kleinen Algebra finden.
1 Schreiben Sie die Gleichung der Linie auf. Wenn Sie bereits die Gleichung der Linie haben, können Sie den y-Abschnitt mit einer kleinen Algebra finden.  2 Stellvertreter 0 für x. Die y-Achse ist eine vertikale Linie entlang x = 0. Dies bedeutet, dass jeder Punkt auf der y-Achse eine x-Koordinate von 0 hat, einschließlich des y-Schnittpunkts der Linie.Stecken Sie 0 für x in die Liniengleichung ein.
2 Stellvertreter 0 für x. Die y-Achse ist eine vertikale Linie entlang x = 0. Dies bedeutet, dass jeder Punkt auf der y-Achse eine x-Koordinate von 0 hat, einschließlich des y-Schnittpunkts der Linie.Stecken Sie 0 für x in die Liniengleichung ein.  3 Löse für y. Die Antwort ist der y-Schnittpunkt der Linie.
3 Löse für y. Die Antwort ist der y-Schnittpunkt der Linie.  4 Bestätigen Sie mit der grafischen Darstellung (optional). Um Ihre Antwort zu überprüfen, zeichnen Sie die Gleichung so gut wie möglich auf. Der Punkt, an dem die Linie die y-Achse kreuzt, ist der y-Achsenabschnitt.
4 Bestätigen Sie mit der grafischen Darstellung (optional). Um Ihre Antwort zu überprüfen, zeichnen Sie die Gleichung so gut wie möglich auf. Der Punkt, an dem die Linie die y-Achse kreuzt, ist der y-Achsenabschnitt.  5 Finde den y-Achsenabschnitt für eine quadratische Gleichung. Eine quadratische Gleichung enthält eine Variable (x oder y), die auf die Potenz von 2 erhöht wird. Sie können mit derselben Substitution nach y auflösen, aber da die Quadra- te eine Kurve beschreibt, könnte sie die y-Achse bei 0, 1 oder 2 abfangen Punkte. Das bedeutet, dass Sie mit 0, 1 oder 2 Antworten enden können.
5 Finde den y-Achsenabschnitt für eine quadratische Gleichung. Eine quadratische Gleichung enthält eine Variable (x oder y), die auf die Potenz von 2 erhöht wird. Sie können mit derselben Substitution nach y auflösen, aber da die Quadra- te eine Kurve beschreibt, könnte sie die y-Achse bei 0, 1 oder 2 abfangen Punkte. Das bedeutet, dass Sie mit 0, 1 oder 2 Antworten enden können.