Der Maßstabsfaktor oder der lineare Maßstabsfaktor ist das Verhältnis von zwei entsprechenden Seitenlängen ähnlicher Figuren. Ähnliche Figuren haben die gleiche Form, sind aber unterschiedlich groß. Der Skalierungsfaktor wird verwendet, um grundlegende geometrische Probleme zu lösen. Sie können den Skalierungsfaktor verwenden, um die fehlenden Seitenlängen einer Figur zu finden. Umgekehrt können Sie die Seitenlängen von zwei ähnlichen Figuren verwenden, um den Skalierungsfaktor zu berechnen. Diese Probleme erfordern Multiplikation oder erfordern, dass Sie Brüche vereinfachen.
Methode eins von vier:
Den Skalierungsfaktor für ähnliche Figuren finden
-
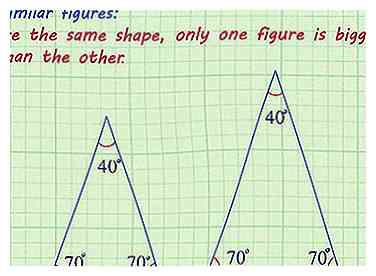 1 Stellen Sie sicher, dass die Zahlen ähnlich sind. Ähnliche Figuren oder Formen sind solche, bei denen die Winkel kongruent sind und die Seitenlängen proportional sind. Ähnliche Figuren haben die gleiche Form, nur eine Figur ist größer als die andere.[1]
1 Stellen Sie sicher, dass die Zahlen ähnlich sind. Ähnliche Figuren oder Formen sind solche, bei denen die Winkel kongruent sind und die Seitenlängen proportional sind. Ähnliche Figuren haben die gleiche Form, nur eine Figur ist größer als die andere.[1] - Das Problem sollte Ihnen sagen, dass die Formen ähnlich sind, oder es kann Ihnen zeigen, dass die Winkel gleich sind, und anderenfalls angeben, dass die Seitenlängen proportional sind, skalieren oder dass sie einander entsprechen.
-
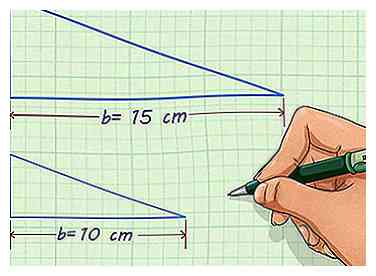 2 Finden Sie auf jeder Figur eine entsprechende Seitenlänge. Möglicherweise müssen Sie die Figur drehen oder spiegeln, sodass die beiden Formen ausgerichtet sind und Sie die entsprechenden Seitenlängen erkennen können. Sie sollten die Länge dieser beiden Seiten erhalten oder in der Lage sein, sie zu messen.[2] Wenn Sie nicht mindestens eine Seitenlänge jeder Figur kennen, können Sie den Skalierungsfaktor nicht finden.
2 Finden Sie auf jeder Figur eine entsprechende Seitenlänge. Möglicherweise müssen Sie die Figur drehen oder spiegeln, sodass die beiden Formen ausgerichtet sind und Sie die entsprechenden Seitenlängen erkennen können. Sie sollten die Länge dieser beiden Seiten erhalten oder in der Lage sein, sie zu messen.[2] Wenn Sie nicht mindestens eine Seitenlänge jeder Figur kennen, können Sie den Skalierungsfaktor nicht finden. - Zum Beispiel könnten Sie ein Dreieck mit einer Basis von 15 cm Länge und ein ähnliches Dreieck mit einer Basis von 10 cm Länge haben.
-
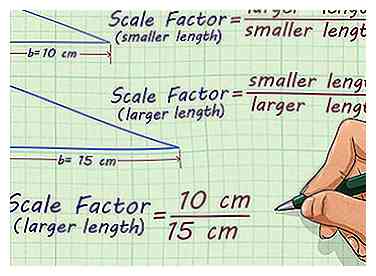 3 Richten Sie ein Verhältnis ein. Für jedes Paar ähnlicher Figuren gibt es zwei Skalierungsfaktoren: einen, den Sie beim Skalieren verwenden, und einen, den Sie beim Skalieren verwenden. Wenn Sie von einer kleineren zu einer größeren Figur skalieren, verwenden Sie das Verhältnis . Wenn Sie von einer größeren Figur zu einer kleineren Figur verkleinern, verwenden Sie das Verhältnis .[3]
3 Richten Sie ein Verhältnis ein. Für jedes Paar ähnlicher Figuren gibt es zwei Skalierungsfaktoren: einen, den Sie beim Skalieren verwenden, und einen, den Sie beim Skalieren verwenden. Wenn Sie von einer kleineren zu einer größeren Figur skalieren, verwenden Sie das Verhältnis . Wenn Sie von einer größeren Figur zu einer kleineren Figur verkleinern, verwenden Sie das Verhältnis .[3] - Wenn Sie zum Beispiel von einem Dreieck mit einer 15 cm Basis zu einem mit einer 10 cm Basis skalieren, würden Sie das Verhältnis verwenden .
Wenn Sie die entsprechenden Werte eingeben, wird es .
- Wenn Sie zum Beispiel von einem Dreieck mit einer 15 cm Basis zu einem mit einer 10 cm Basis skalieren, würden Sie das Verhältnis verwenden .
-
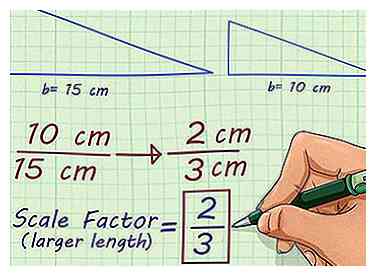 4 Vereinfachen Sie das Verhältnis. Das vereinfachte Verhältnis oder die Fraktion geben Ihnen Ihren Skalierungsfaktor. Wenn Sie verkleinern, wird Ihr Skalierungsfaktor ein richtiger Bruch sein.[4] Wenn Sie hochskalieren, wird es eine ganze Zahl oder ein unechter Bruch sein, den Sie in eine Dezimalzahl umwandeln können.
4 Vereinfachen Sie das Verhältnis. Das vereinfachte Verhältnis oder die Fraktion geben Ihnen Ihren Skalierungsfaktor. Wenn Sie verkleinern, wird Ihr Skalierungsfaktor ein richtiger Bruch sein.[4] Wenn Sie hochskalieren, wird es eine ganze Zahl oder ein unechter Bruch sein, den Sie in eine Dezimalzahl umwandeln können. - Zum Beispiel das Verhältnis vereinfacht zu . So ist der Skalenfaktor von zwei Dreiecken, eines mit einer Basis von 15 cm und eines mit einer Basis von 10 cm .
Methode zwei von vier:
Eine ähnliche Figur mit dem Skalierungsfaktor finden
-
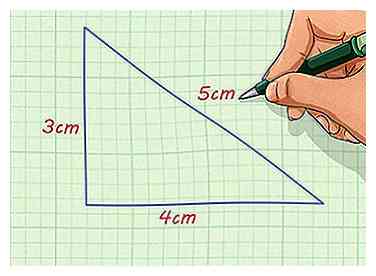 1 Finde die Seitenlängen der Figur. Sie sollten eine Figur haben, deren Seitenlängen angegeben oder messbar sind. Wenn Sie die Seitenlängen der Figur nicht bestimmen können, können Sie keine ähnliche Figur machen.
1 Finde die Seitenlängen der Figur. Sie sollten eine Figur haben, deren Seitenlängen angegeben oder messbar sind. Wenn Sie die Seitenlängen der Figur nicht bestimmen können, können Sie keine ähnliche Figur machen. - Zum Beispiel könnten Sie ein rechtwinkliges Dreieck mit Seiten von 4 cm und 3 cm und eine Hypotenuse von 5 cm Länge haben.
-
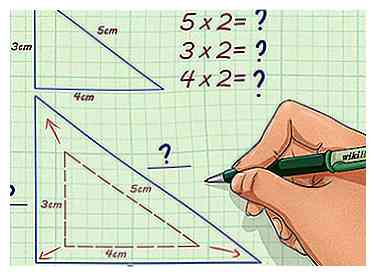 2 Bestimmen Sie, ob Sie nach oben oder unten skalieren. Wenn Sie skalieren, wird Ihre fehlende Zahl größer und der Skalierungsfaktor wird eine ganze Zahl, ein falscher Bruch oder eine Dezimalzahl sein. Wenn Sie verkleinern, wird Ihre fehlende Zahl kleiner und Ihr Skalierungsfaktor wird höchstwahrscheinlich ein richtiger Bruch sein.
2 Bestimmen Sie, ob Sie nach oben oder unten skalieren. Wenn Sie skalieren, wird Ihre fehlende Zahl größer und der Skalierungsfaktor wird eine ganze Zahl, ein falscher Bruch oder eine Dezimalzahl sein. Wenn Sie verkleinern, wird Ihre fehlende Zahl kleiner und Ihr Skalierungsfaktor wird höchstwahrscheinlich ein richtiger Bruch sein. - Wenn der Skalierungsfaktor beispielsweise 2 ist, werden Sie skaliert, und die ähnliche Zahl ist größer als die, die Sie haben.
-
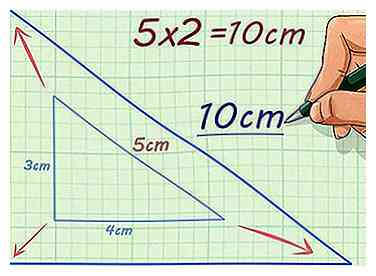 3 Multiplizieren Sie eine Seitenlänge mit dem Skalierungsfaktor. Der Skalierungsfaktor sollte Ihnen gegeben werden. Wenn Sie die Seitenlänge mit dem Skalierungsfaktor multiplizieren, erhalten Sie die fehlende entsprechende Seitenlänge auf der ähnlichen Figur.[5]
3 Multiplizieren Sie eine Seitenlänge mit dem Skalierungsfaktor. Der Skalierungsfaktor sollte Ihnen gegeben werden. Wenn Sie die Seitenlänge mit dem Skalierungsfaktor multiplizieren, erhalten Sie die fehlende entsprechende Seitenlänge auf der ähnlichen Figur.[5] - Wenn zum Beispiel die Hypotenuse eines rechtwinkligen Dreiecks 5 cm lang ist und der Skalierungsfaktor 2, um die Hypotenuse des ähnlichen Dreiecks zu finden, würden Sie berechnen . Das ähnliche Dreieck hat also eine Hypotenuse, die 10 cm lang ist.
-
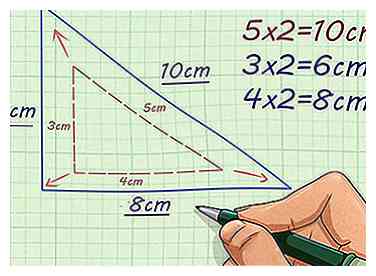 4 Finde die verbleibenden Seitenlängen der Figur. Fahren Sie fort, jede Seitenlänge mit dem Skalierungsfaktor zu multiplizieren. Dadurch erhalten Sie die entsprechenden Seitenlängen der fehlenden Figur.
4 Finde die verbleibenden Seitenlängen der Figur. Fahren Sie fort, jede Seitenlänge mit dem Skalierungsfaktor zu multiplizieren. Dadurch erhalten Sie die entsprechenden Seitenlängen der fehlenden Figur. - Zum Beispiel, wenn die Basis eines rechtwinkligen Dreiecks 3 cm lang ist, mit einem Skalierungsfaktor von 2, würden Sie berechnen um die Basis des ähnlichen Dreiecks zu finden. Wenn die Höhe eines rechtwinkligen Dreiecks 4 cm lang ist, würden Sie mit einem Skalierungsfaktor von 2 rechnen um die Höhe des ähnlichen Dreiecks zu finden.
Methode drei von vier:
Abschließen von Beispielproblemen
-
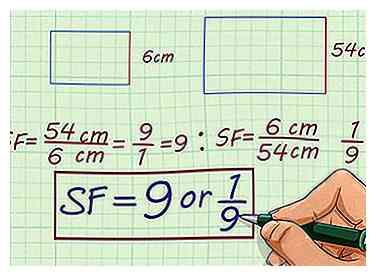 1 Finden Sie den Skalierungsfaktor dieser ähnlichen Zahlen: ein Rechteck mit einer Höhe von 6 cm und ein Rechteck mit einer Höhe von 54 cm.
1 Finden Sie den Skalierungsfaktor dieser ähnlichen Zahlen: ein Rechteck mit einer Höhe von 6 cm und ein Rechteck mit einer Höhe von 54 cm. - Erstellen Sie ein Verhältnis zwischen den beiden Höhen. Scaling up, das Verhältnis ist . Herunterskalieren ist das Verhältnis .
- Vereinfachen Sie das Verhältnis. Das Verhältnis vereinfacht zu . Das Verhältnis vereinfacht zu . Die beiden Rechtecke haben also einen Skalierungsfaktor von oder .
-
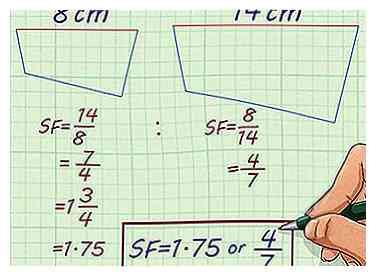 2 Versuchen Sie dieses Problem. Ein unregelmäßiges Polygon ist an seiner breitesten Stelle 14 cm lang. Ein ähnliches unregelmäßiges Polygon ist 8 Zoll an seiner breitesten Stelle. Was ist der Skalierungsfaktor?
2 Versuchen Sie dieses Problem. Ein unregelmäßiges Polygon ist an seiner breitesten Stelle 14 cm lang. Ein ähnliches unregelmäßiges Polygon ist 8 Zoll an seiner breitesten Stelle. Was ist der Skalierungsfaktor? - Unregelmäßige Figuren können ähnlich sein, wenn alle Seiten proportional zueinander sind. Auf diese Weise können Sie einen Skalierungsfaktor anhand einer beliebigen Dimension berechnen.[6]
- Da Sie die Breite jedes Polygons kennen, können Sie ein Verhältnis festlegen, indem Sie sie vergleichen. Scaling up, das Verhältnis ist . Herunterskalieren ist das Verhältnis .
- Vereinfachen Sie das Verhältnis. Das Verhältnis vereinfacht zu . Das Verhältnis vereinfacht zu . Also haben die zwei unregelmäßigen Polygone einen Skalierungsfaktor von oder .
-
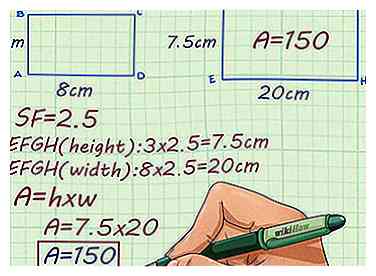 3 Verwenden Sie den Skalierungsfaktor, um dieses Problem zu lösen. Rechteck ABCD ist 8cm x 3cm. Rechteck EFGH ist ein größeres, ähnliches Rechteck. Wie groß ist die Fläche von Rectangle EFGH?
3 Verwenden Sie den Skalierungsfaktor, um dieses Problem zu lösen. Rechteck ABCD ist 8cm x 3cm. Rechteck EFGH ist ein größeres, ähnliches Rechteck. Wie groß ist die Fläche von Rectangle EFGH? - Multiplizieren Sie die Höhe von Rectangle ABCD mit dem Skalierungsfaktor. Dadurch erhalten Sie die Höhe von Rectangle EFGH: .
- Multiplizieren Sie die Breite von Rectangle ABCD mit dem Skalierungsfaktor. Dies gibt Ihnen die Breite von Rectangle EFGH: .
- Multiplizieren Sie die Höhe und Breite von Rectangle EFGH, um den Bereich zu finden: . Die Fläche von Rectangle EFGH beträgt also 150 Quadratzentimeter.
Methode vier von vier:
Den Skalierungsfaktor in der Chemie finden
-
 1 Teile die Molmasse der Verbindung durch die der empirischen Formel. Wenn Sie die empirische Formel einer chemischen Verbindung haben und die Molekülformel derselben chemischen Verbindung finden müssen, können Sie den Skalierungsfaktor finden, den Sie benötigen, indem Sie die Molmasse der Verbindung durch die Molmasse der empirischen Formel dividieren.
1 Teile die Molmasse der Verbindung durch die der empirischen Formel. Wenn Sie die empirische Formel einer chemischen Verbindung haben und die Molekülformel derselben chemischen Verbindung finden müssen, können Sie den Skalierungsfaktor finden, den Sie benötigen, indem Sie die Molmasse der Verbindung durch die Molmasse der empirischen Formel dividieren. - Zum Beispiel müssen Sie möglicherweise die Molmasse einer H2O-Verbindung mit einer Molmasse von 54,05 g / mol finden.
- Die Molmasse von H2O beträgt 18,0152 g / mol.
- Finden Sie den Skalierungsfaktor, indem Sie die Molmasse der Verbindung durch die Molmasse der empirischen Formel dividieren:
- Skalierungsfaktor = 54,05 / 18,0152 = 3
- Zum Beispiel müssen Sie möglicherweise die Molmasse einer H2O-Verbindung mit einer Molmasse von 54,05 g / mol finden.
-
 2 Multiplizieren Sie die empirische Formel mit dem Skalierungsfaktor. Multiplizieren Sie die Indizes jedes Elements innerhalb der empirischen Formel mit dem soeben berechneten Skalierungsfaktor. Dies gibt Ihnen die molekulare Formel der chemischen Verbindungsprobe, die an dem Problem beteiligt ist.
2 Multiplizieren Sie die empirische Formel mit dem Skalierungsfaktor. Multiplizieren Sie die Indizes jedes Elements innerhalb der empirischen Formel mit dem soeben berechneten Skalierungsfaktor. Dies gibt Ihnen die molekulare Formel der chemischen Verbindungsprobe, die an dem Problem beteiligt ist. - Um beispielsweise die Molekülformel der betreffenden Verbindung zu finden, multiplizieren Sie die Indizes von H20 mit dem Skalierungsfaktor von 3.
- H2O * 3 = H6O3
- Um beispielsweise die Molekülformel der betreffenden Verbindung zu finden, multiplizieren Sie die Indizes von H20 mit dem Skalierungsfaktor von 3.
-
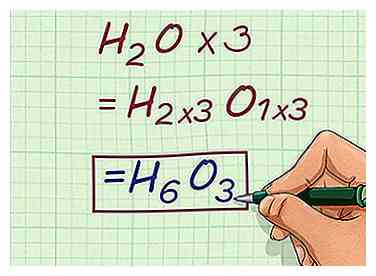 3 Schreibe die Antwort. Mit dieser Antwort haben Sie erfolgreich die Antwort für die empirische Formel sowie die molekulare Formel der chemischen Verbindung gefunden, die an dem Problem beteiligt ist.
3 Schreibe die Antwort. Mit dieser Antwort haben Sie erfolgreich die Antwort für die empirische Formel sowie die molekulare Formel der chemischen Verbindung gefunden, die an dem Problem beteiligt ist. - Zum Beispiel ist der Skalierungsfaktor für die Verbindung 3. Die Molekülformel der Verbindung ist H6O3.
 Minotauromaquia
Minotauromaquia
 1 Stellen Sie sicher, dass die Zahlen ähnlich sind. Ähnliche Figuren oder Formen sind solche, bei denen die Winkel kongruent sind und die Seitenlängen proportional sind. Ähnliche Figuren haben die gleiche Form, nur eine Figur ist größer als die andere.[1]
1 Stellen Sie sicher, dass die Zahlen ähnlich sind. Ähnliche Figuren oder Formen sind solche, bei denen die Winkel kongruent sind und die Seitenlängen proportional sind. Ähnliche Figuren haben die gleiche Form, nur eine Figur ist größer als die andere.[1]  2 Finden Sie auf jeder Figur eine entsprechende Seitenlänge. Möglicherweise müssen Sie die Figur drehen oder spiegeln, sodass die beiden Formen ausgerichtet sind und Sie die entsprechenden Seitenlängen erkennen können. Sie sollten die Länge dieser beiden Seiten erhalten oder in der Lage sein, sie zu messen.[2] Wenn Sie nicht mindestens eine Seitenlänge jeder Figur kennen, können Sie den Skalierungsfaktor nicht finden.
2 Finden Sie auf jeder Figur eine entsprechende Seitenlänge. Möglicherweise müssen Sie die Figur drehen oder spiegeln, sodass die beiden Formen ausgerichtet sind und Sie die entsprechenden Seitenlängen erkennen können. Sie sollten die Länge dieser beiden Seiten erhalten oder in der Lage sein, sie zu messen.[2] Wenn Sie nicht mindestens eine Seitenlänge jeder Figur kennen, können Sie den Skalierungsfaktor nicht finden.  3 Richten Sie ein Verhältnis ein. Für jedes Paar ähnlicher Figuren gibt es zwei Skalierungsfaktoren: einen, den Sie beim Skalieren verwenden, und einen, den Sie beim Skalieren verwenden. Wenn Sie von einer kleineren zu einer größeren Figur skalieren, verwenden Sie das Verhältnis
3 Richten Sie ein Verhältnis ein. Für jedes Paar ähnlicher Figuren gibt es zwei Skalierungsfaktoren: einen, den Sie beim Skalieren verwenden, und einen, den Sie beim Skalieren verwenden. Wenn Sie von einer kleineren zu einer größeren Figur skalieren, verwenden Sie das Verhältnis  4 Vereinfachen Sie das Verhältnis. Das vereinfachte Verhältnis oder die Fraktion geben Ihnen Ihren Skalierungsfaktor. Wenn Sie verkleinern, wird Ihr Skalierungsfaktor ein richtiger Bruch sein.[4] Wenn Sie hochskalieren, wird es eine ganze Zahl oder ein unechter Bruch sein, den Sie in eine Dezimalzahl umwandeln können.
4 Vereinfachen Sie das Verhältnis. Das vereinfachte Verhältnis oder die Fraktion geben Ihnen Ihren Skalierungsfaktor. Wenn Sie verkleinern, wird Ihr Skalierungsfaktor ein richtiger Bruch sein.[4] Wenn Sie hochskalieren, wird es eine ganze Zahl oder ein unechter Bruch sein, den Sie in eine Dezimalzahl umwandeln können.  1 Finde die Seitenlängen der Figur. Sie sollten eine Figur haben, deren Seitenlängen angegeben oder messbar sind. Wenn Sie die Seitenlängen der Figur nicht bestimmen können, können Sie keine ähnliche Figur machen.
1 Finde die Seitenlängen der Figur. Sie sollten eine Figur haben, deren Seitenlängen angegeben oder messbar sind. Wenn Sie die Seitenlängen der Figur nicht bestimmen können, können Sie keine ähnliche Figur machen.  2 Bestimmen Sie, ob Sie nach oben oder unten skalieren. Wenn Sie skalieren, wird Ihre fehlende Zahl größer und der Skalierungsfaktor wird eine ganze Zahl, ein falscher Bruch oder eine Dezimalzahl sein. Wenn Sie verkleinern, wird Ihre fehlende Zahl kleiner und Ihr Skalierungsfaktor wird höchstwahrscheinlich ein richtiger Bruch sein.
2 Bestimmen Sie, ob Sie nach oben oder unten skalieren. Wenn Sie skalieren, wird Ihre fehlende Zahl größer und der Skalierungsfaktor wird eine ganze Zahl, ein falscher Bruch oder eine Dezimalzahl sein. Wenn Sie verkleinern, wird Ihre fehlende Zahl kleiner und Ihr Skalierungsfaktor wird höchstwahrscheinlich ein richtiger Bruch sein.  3 Multiplizieren Sie eine Seitenlänge mit dem Skalierungsfaktor. Der Skalierungsfaktor sollte Ihnen gegeben werden. Wenn Sie die Seitenlänge mit dem Skalierungsfaktor multiplizieren, erhalten Sie die fehlende entsprechende Seitenlänge auf der ähnlichen Figur.[5]
3 Multiplizieren Sie eine Seitenlänge mit dem Skalierungsfaktor. Der Skalierungsfaktor sollte Ihnen gegeben werden. Wenn Sie die Seitenlänge mit dem Skalierungsfaktor multiplizieren, erhalten Sie die fehlende entsprechende Seitenlänge auf der ähnlichen Figur.[5]  4 Finde die verbleibenden Seitenlängen der Figur. Fahren Sie fort, jede Seitenlänge mit dem Skalierungsfaktor zu multiplizieren. Dadurch erhalten Sie die entsprechenden Seitenlängen der fehlenden Figur.
4 Finde die verbleibenden Seitenlängen der Figur. Fahren Sie fort, jede Seitenlänge mit dem Skalierungsfaktor zu multiplizieren. Dadurch erhalten Sie die entsprechenden Seitenlängen der fehlenden Figur.  1 Finden Sie den Skalierungsfaktor dieser ähnlichen Zahlen: ein Rechteck mit einer Höhe von 6 cm und ein Rechteck mit einer Höhe von 54 cm.
1 Finden Sie den Skalierungsfaktor dieser ähnlichen Zahlen: ein Rechteck mit einer Höhe von 6 cm und ein Rechteck mit einer Höhe von 54 cm.  2 Versuchen Sie dieses Problem. Ein unregelmäßiges Polygon ist an seiner breitesten Stelle 14 cm lang. Ein ähnliches unregelmäßiges Polygon ist 8 Zoll an seiner breitesten Stelle. Was ist der Skalierungsfaktor?
2 Versuchen Sie dieses Problem. Ein unregelmäßiges Polygon ist an seiner breitesten Stelle 14 cm lang. Ein ähnliches unregelmäßiges Polygon ist 8 Zoll an seiner breitesten Stelle. Was ist der Skalierungsfaktor?  3 Verwenden Sie den Skalierungsfaktor, um dieses Problem zu lösen. Rechteck ABCD ist 8cm x 3cm. Rechteck EFGH ist ein größeres, ähnliches Rechteck. Wie groß ist die Fläche von Rectangle EFGH?
3 Verwenden Sie den Skalierungsfaktor, um dieses Problem zu lösen. Rechteck ABCD ist 8cm x 3cm. Rechteck EFGH ist ein größeres, ähnliches Rechteck. Wie groß ist die Fläche von Rectangle EFGH?  1 Teile die Molmasse der Verbindung durch die der empirischen Formel. Wenn Sie die empirische Formel einer chemischen Verbindung haben und die Molekülformel derselben chemischen Verbindung finden müssen, können Sie den Skalierungsfaktor finden, den Sie benötigen, indem Sie die Molmasse der Verbindung durch die Molmasse der empirischen Formel dividieren.
1 Teile die Molmasse der Verbindung durch die der empirischen Formel. Wenn Sie die empirische Formel einer chemischen Verbindung haben und die Molekülformel derselben chemischen Verbindung finden müssen, können Sie den Skalierungsfaktor finden, den Sie benötigen, indem Sie die Molmasse der Verbindung durch die Molmasse der empirischen Formel dividieren.  2 Multiplizieren Sie die empirische Formel mit dem Skalierungsfaktor. Multiplizieren Sie die Indizes jedes Elements innerhalb der empirischen Formel mit dem soeben berechneten Skalierungsfaktor. Dies gibt Ihnen die molekulare Formel der chemischen Verbindungsprobe, die an dem Problem beteiligt ist.
2 Multiplizieren Sie die empirische Formel mit dem Skalierungsfaktor. Multiplizieren Sie die Indizes jedes Elements innerhalb der empirischen Formel mit dem soeben berechneten Skalierungsfaktor. Dies gibt Ihnen die molekulare Formel der chemischen Verbindungsprobe, die an dem Problem beteiligt ist. 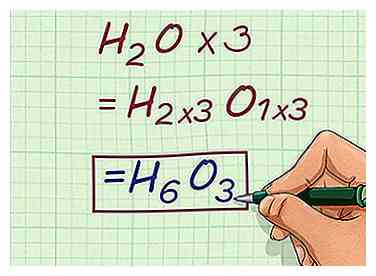 3 Schreibe die Antwort. Mit dieser Antwort haben Sie erfolgreich die Antwort für die empirische Formel sowie die molekulare Formel der chemischen Verbindung gefunden, die an dem Problem beteiligt ist.
3 Schreibe die Antwort. Mit dieser Antwort haben Sie erfolgreich die Antwort für die empirische Formel sowie die molekulare Formel der chemischen Verbindung gefunden, die an dem Problem beteiligt ist.