Ein Vielfaches ist das Ergebnis der Multiplikation einer Zahl mit einer Ganzzahl. Das kleinste gemeinsame Vielfache (LCM) einer Gruppe von Zahlen ist die kleinste Zahl, die ein Vielfaches aller Zahlen ist. Um das kleinste gemeinsame Vielfache zu finden, müssen Sie in der Lage sein, die Faktoren der Zahlen zu identifizieren, mit denen Sie arbeiten. Sie können einige verschiedene Methoden verwenden, um das kleinste gemeinsame Vielfache zu finden. Diese Methoden funktionieren auch, wenn das LCM aus mehr als zwei Zahlen besteht.
Methode eins von vier:
Auflistung aller Multiples
-
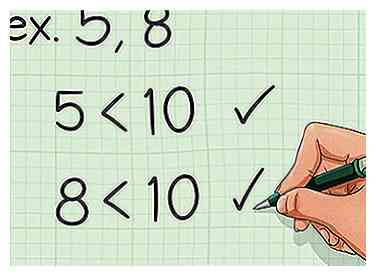 1 Bewerte deine Zahlen. Diese Methode funktioniert am besten, wenn Sie mit zwei Zahlen arbeiten, die kleiner als 10 sind. Wenn Sie mit größeren Zahlen arbeiten, empfiehlt es sich, eine andere Methode zu verwenden.
1 Bewerte deine Zahlen. Diese Methode funktioniert am besten, wenn Sie mit zwei Zahlen arbeiten, die kleiner als 10 sind. Wenn Sie mit größeren Zahlen arbeiten, empfiehlt es sich, eine andere Methode zu verwenden. - Zum Beispiel müssen Sie möglicherweise das kleinste gemeinsame Vielfache von 5 und 8 finden. Da dies kleine Zahlen sind, ist es angemessen, diese Methode zu verwenden.
-
 2 Schreiben Sie die ersten mehreren Vielfachen der ersten Zahl aus. Ein Vielfaches ist ein Produkt einer beliebigen Zahl und einer ganzen Zahl.[1] Mit anderen Worten, sie sind die Zahlen, die Sie in einer Multiplikationstabelle sehen würden.
2 Schreiben Sie die ersten mehreren Vielfachen der ersten Zahl aus. Ein Vielfaches ist ein Produkt einer beliebigen Zahl und einer ganzen Zahl.[1] Mit anderen Worten, sie sind die Zahlen, die Sie in einer Multiplikationstabelle sehen würden. - Zum Beispiel sind die ersten mehreren Vielfachen von 5 5, 10, 15, 20, 25, 30, 35 und 40.
-
 3 Schreibe die ersten paar Vielfachen der zweiten Zahl aus. Tun Sie dies in der Nähe der ersten Menge von Vielfachen, so dass sie leicht zu vergleichen sind.
3 Schreibe die ersten paar Vielfachen der zweiten Zahl aus. Tun Sie dies in der Nähe der ersten Menge von Vielfachen, so dass sie leicht zu vergleichen sind. - Zum Beispiel sind die ersten mehreren Vielfachen von 8 8, 16, 24, 32, 40, 48, 56 und 64.
-
 4 Finde das kleinste Vielfache, das die Zahlen gemeinsam haben. Möglicherweise müssen Sie Ihre Liste der Vielfachen erweitern, bis Sie eine der beiden Nummern finden. Diese Nummer ist Ihr am wenigsten gewöhnliches Vielfaches.[2]
4 Finde das kleinste Vielfache, das die Zahlen gemeinsam haben. Möglicherweise müssen Sie Ihre Liste der Vielfachen erweitern, bis Sie eine der beiden Nummern finden. Diese Nummer ist Ihr am wenigsten gewöhnliches Vielfaches.[2] - Zum Beispiel ist der niedrigste Vielfache 5 und 8 Anteil 40, so dass das kleinste gemeinsame Vielfache von 5 und 8 40 ist.
Methode zwei von vier:
Verwenden der Primfaktorzerlegung
-
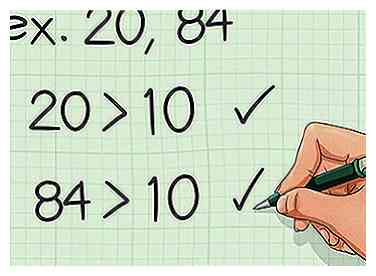 1 Bewerte deine Zahlen. Diese Methode funktioniert am besten, wenn beide Zahlen, mit denen Sie arbeiten, größer als 10 sind. Wenn Sie kleinere Zahlen haben, können Sie eine andere Methode verwenden, um das am wenigsten häufige Vielfache schneller zu finden.
1 Bewerte deine Zahlen. Diese Methode funktioniert am besten, wenn beide Zahlen, mit denen Sie arbeiten, größer als 10 sind. Wenn Sie kleinere Zahlen haben, können Sie eine andere Methode verwenden, um das am wenigsten häufige Vielfache schneller zu finden. - Wenn Sie beispielsweise das kleinste gemeinsame Vielfache von 20 und 84 suchen müssen, sollten Sie diese Methode verwenden.
-
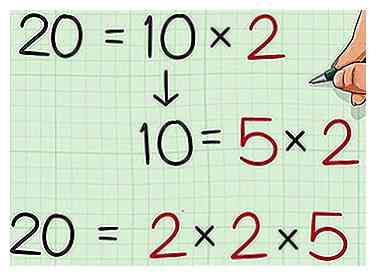 2 Faktor die erste Zahl. Sie möchten die Zahl in ihre Primfaktoren einteilen; Finde die Primfaktoren, die du multiplizieren kannst, um diese Zahl zu erhalten. Eine Möglichkeit besteht darin, einen Faktorenbaum zu erstellen. Sobald Sie mit dem Faktorisieren fertig sind, schreiben Sie die Primfaktoren als Gleichung neu.
2 Faktor die erste Zahl. Sie möchten die Zahl in ihre Primfaktoren einteilen; Finde die Primfaktoren, die du multiplizieren kannst, um diese Zahl zu erhalten. Eine Möglichkeit besteht darin, einen Faktorenbaum zu erstellen. Sobald Sie mit dem Faktorisieren fertig sind, schreiben Sie die Primfaktoren als Gleichung neu. - Beispielsweise, und , also die Primfaktoren von 20 sind 2, 2 und 5. Das Umschreiben als Gleichung erhält man .
-
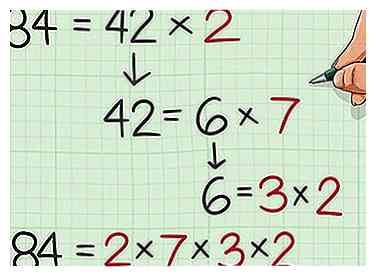 3 Faktor die zweite Zahl. Tun Sie dies auf die gleiche Weise, wie Sie die erste Zahl berechnet haben, indem Sie die Primfaktoren finden, die Sie zusammen multiplizieren können, um die Zahl zu erhalten.
3 Faktor die zweite Zahl. Tun Sie dies auf die gleiche Weise, wie Sie die erste Zahl berechnet haben, indem Sie die Primfaktoren finden, die Sie zusammen multiplizieren können, um die Zahl zu erhalten. - Beispielsweise, , , und Die Hauptfaktoren von 84 sind also 2, 7, 3 und 2. Das Umschreiben als Gleichung erhält man .
-
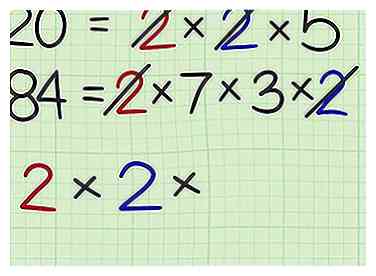 4 Notieren Sie die Faktoren für jede Anzahl Aktien. Schreiben Sie die Faktoren als Multiplikationssatz. Wenn Sie jeden Faktor schreiben, kreuzen Sie ihn in jeder Zahlenfaktorisierungsgleichung an.
4 Notieren Sie die Faktoren für jede Anzahl Aktien. Schreiben Sie die Faktoren als Multiplikationssatz. Wenn Sie jeden Faktor schreiben, kreuzen Sie ihn in jeder Zahlenfaktorisierungsgleichung an. - Zum Beispiel teilen beide Zahlen einen Faktor von 2, also schreibe und streichen Sie eine 2 in jeder Faktorisierungsgleichung.
- Jede Zahl teilt sich auch eine zweite 2, also ändern Sie den Multiplikationssatz zu und streichen Sie eine zweite 2 in jeder Faktorisierungsgleichung.
-
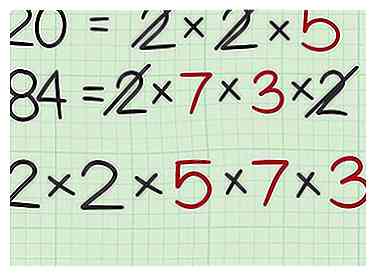 5 Fügen Sie dem Multiplikationssatz alle übrig gebliebenen Faktoren hinzu. Dies sind die Faktoren, die Sie beim Vergleich der beiden Gruppen von Faktoren nicht durchkreuzt haben. Dies sind also Faktoren, die die beiden Zahlen nicht teilen.[3]
5 Fügen Sie dem Multiplikationssatz alle übrig gebliebenen Faktoren hinzu. Dies sind die Faktoren, die Sie beim Vergleich der beiden Gruppen von Faktoren nicht durchkreuzt haben. Dies sind also Faktoren, die die beiden Zahlen nicht teilen.[3] - Zum Beispiel in der Gleichung , du hast beide 2s durchgestrichen, da diese Faktoren mit der anderen Zahl geteilt wurden. Sie haben einen Faktor von 5 übrig, fügen Sie das also zu Ihrem Multiplikationssatz hinzu: .
- In der Gleichung , du hast auch beide 2s durchgestrichen. Sie haben die Faktoren 7 und 3 übrig, also fügen Sie diese zu Ihrem Multiplikationssatz hinzu: .
-
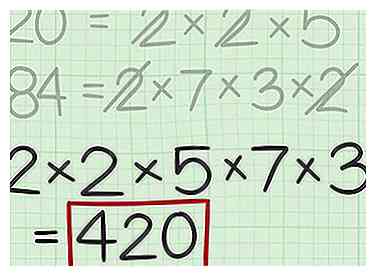 6 Berechnen Sie das kleinste gemeinsame Vielfache. Multiplizieren Sie dazu alle Faktoren in Ihrem Multiplikationssatz.
6 Berechnen Sie das kleinste gemeinsame Vielfache. Multiplizieren Sie dazu alle Faktoren in Ihrem Multiplikationssatz. - Beispielsweise, . Das kleinste gemeinsame Vielfache von 20 und 84 ist also 420.
Methode drei von vier:
Verwenden der Gitter- oder Ladder-Methode
-
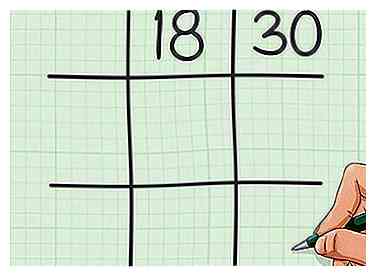 1 Zeichnen Sie ein Tic-Tac-Toe-Raster. Ein Tic-Tac-Toe-Gitter besteht aus zwei parallelen Linien, die sich senkrecht schneiden. Die Zeilen bilden drei Zeilen und drei Spalten und sehen aus wie die Rautetaste (#) auf einem Telefon oder einer Tastatur. Schreiben Sie Ihre erste Zahl in das oberste Quadrat des Gitters. Schreibe deine zweite Zahl in das obere rechte Feld des Rasters.[4]
1 Zeichnen Sie ein Tic-Tac-Toe-Raster. Ein Tic-Tac-Toe-Gitter besteht aus zwei parallelen Linien, die sich senkrecht schneiden. Die Zeilen bilden drei Zeilen und drei Spalten und sehen aus wie die Rautetaste (#) auf einem Telefon oder einer Tastatur. Schreiben Sie Ihre erste Zahl in das oberste Quadrat des Gitters. Schreibe deine zweite Zahl in das obere rechte Feld des Rasters.[4] - Wenn Sie beispielsweise versuchen, das kleinste gemeinsame Vielfache von 18 und 30 zu finden, schreiben Sie 18 in die obere Mitte Ihres Rasters und 30 in die obere rechte Ecke Ihres Rasters.
-
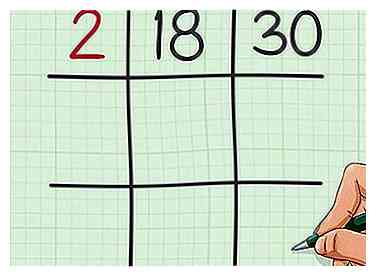 2 Suchen Sie nach einem Faktor, der beiden Zahlen gemeinsam ist. Schreiben Sie diese Zahl in das obere linke Quadrat Ihres Rasters. Es ist hilfreich, Primfaktoren zu verwenden, aber das muss nicht unbedingt sein.
2 Suchen Sie nach einem Faktor, der beiden Zahlen gemeinsam ist. Schreiben Sie diese Zahl in das obere linke Quadrat Ihres Rasters. Es ist hilfreich, Primfaktoren zu verwenden, aber das muss nicht unbedingt sein. - Zum Beispiel, da 18 und 30 beide gerade Zahlen sind, wissen Sie, dass sie beide einen Faktor 2 haben.Schreiben Sie 2 oben links in das Raster.
-
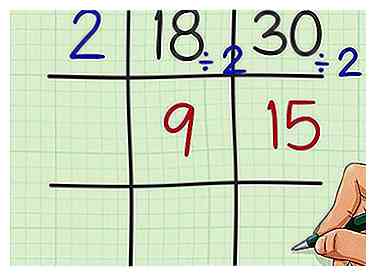 3 Unterteilen Sie den Faktor in jede Zahl. Schreibe den Quotienten in das Quadrat unter jeder Zahl. Ein Quotient ist die Antwort auf ein Teilungsproblem.
3 Unterteilen Sie den Faktor in jede Zahl. Schreibe den Quotienten in das Quadrat unter jeder Zahl. Ein Quotient ist die Antwort auf ein Teilungsproblem. - Beispielsweise, , also schreibe 9 unter 18 in das Raster.
- schreib also 15 unter 30 in das Raster.
-
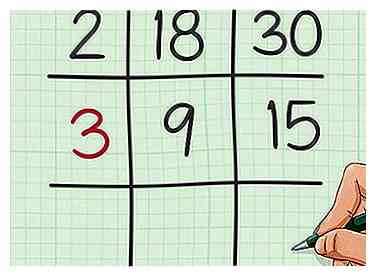 4 Finden Sie einen Faktor, der den beiden Quotienten gemeinsam ist. Wenn für beide Quotienten kein Faktor vorhanden ist, können Sie diesen und den nächsten Schritt überspringen. Wenn es einen gemeinsamen Faktor gibt, schreibe es in das mittlere linke Quadrat des Rasters.
4 Finden Sie einen Faktor, der den beiden Quotienten gemeinsam ist. Wenn für beide Quotienten kein Faktor vorhanden ist, können Sie diesen und den nächsten Schritt überspringen. Wenn es einen gemeinsamen Faktor gibt, schreibe es in das mittlere linke Quadrat des Rasters. - Zum Beispiel haben 9 und 15 beide einen Faktor von 3, also würden Sie 3 in der Mitte links vom Gitter schreiben.
-
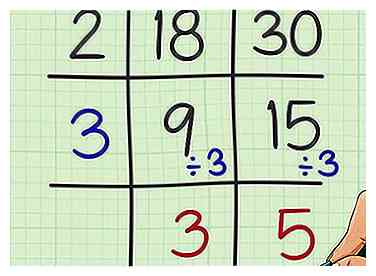 5 Teilen Sie diesen neuen Faktor in jeden Quotienten ein. Schreiben Sie diesen neuen Quotienten unter die ersten.
5 Teilen Sie diesen neuen Faktor in jeden Quotienten ein. Schreiben Sie diesen neuen Quotienten unter die ersten. - Beispielsweise, , also schreibe 3 unter 9 in das Raster.
- Schreibe 5 unter 15 in das Raster.
-
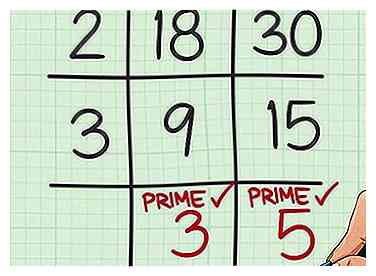 6 Erweitern Sie bei Bedarf Ihr Raster. Folgen Sie diesem Vorgang, bis Sie einen Punkt erreicht haben, an dem die letzten Quotienten keinen gemeinsamen Faktor haben.
6 Erweitern Sie bei Bedarf Ihr Raster. Folgen Sie diesem Vorgang, bis Sie einen Punkt erreicht haben, an dem die letzten Quotienten keinen gemeinsamen Faktor haben. -
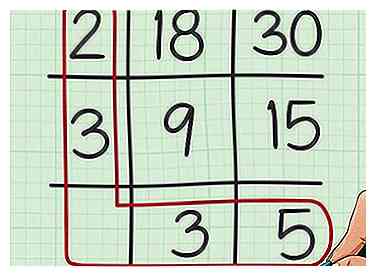 7 Zeichnen Sie einen Kreis um die Zahlen in der ersten Spalte und der letzten Zeile Ihres Rasters. Sie können sich das so vorstellen, als würden Sie ein "L" für "geringstes gemeinsames Vielfaches" zeichnen. Schreiben Sie einen Multiplikationssatz mit all diesen Faktoren.[5]
7 Zeichnen Sie einen Kreis um die Zahlen in der ersten Spalte und der letzten Zeile Ihres Rasters. Sie können sich das so vorstellen, als würden Sie ein "L" für "geringstes gemeinsames Vielfaches" zeichnen. Schreiben Sie einen Multiplikationssatz mit all diesen Faktoren.[5] - Da zum Beispiel 2 und 3 in der ersten Spalte des Rasters stehen und 3 und 5 in der letzten Zeile des Rasters stehen, würden Sie den Satz schreiben .
-
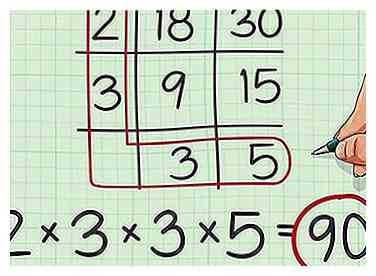 8 Beende die Multiplikation. Wenn Sie alle diese Faktoren zusammen multiplizieren, ist das Ergebnis das kleinste gemeinsame Vielfache Ihrer zwei ursprünglichen Zahlen.[6]
8 Beende die Multiplikation. Wenn Sie alle diese Faktoren zusammen multiplizieren, ist das Ergebnis das kleinste gemeinsame Vielfache Ihrer zwei ursprünglichen Zahlen.[6] - Beispielsweise, . Das kleinste gemeinsame Vielfache von 18 und 30 ist also 90.
Methode vier von vier:
Verwenden des Euklid-Algorithmus
-
 1 Verstehe das Vokabular der Teilung. Die Dividende ist die Nummer, die geteilt wird. Der Divisor ist die Zahl, um die die Dividende geteilt wird. Der Quotient ist die Antwort auf das Teilungsproblem. Der Rest ist der Betrag, der übrig bleibt, nachdem eine Zahl durch eine andere geteilt wurde.[7]
1 Verstehe das Vokabular der Teilung. Die Dividende ist die Nummer, die geteilt wird. Der Divisor ist die Zahl, um die die Dividende geteilt wird. Der Quotient ist die Antwort auf das Teilungsproblem. Der Rest ist der Betrag, der übrig bleibt, nachdem eine Zahl durch eine andere geteilt wurde.[7] - Zum Beispiel in der Gleichung :
15 ist die Dividende
6 ist der Teiler
2 ist der Quotient
3 ist der Rest.
- Zum Beispiel in der Gleichung :
-
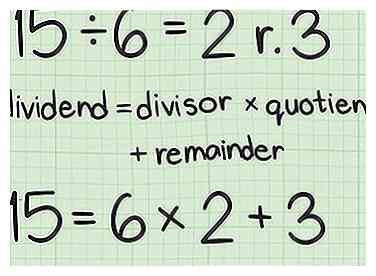 2 Richten Sie die Formel für die Quotienten-Rest-Form ein. Die Formel ist .[8] Sie verwenden dieses Formular, um den Euklid-Algorithmus einzurichten, um den größten gemeinsamen Teiler von zwei Zahlen zu finden.
2 Richten Sie die Formel für die Quotienten-Rest-Form ein. Die Formel ist .[8] Sie verwenden dieses Formular, um den Euklid-Algorithmus einzurichten, um den größten gemeinsamen Teiler von zwei Zahlen zu finden. - Beispielsweise, .
- Der größte gemeinsame Teiler ist der größte Teiler oder Faktor, den zwei Zahlen teilen.[9]
- Bei dieser Methode finden Sie zuerst den größten gemeinsamen Teiler und verwenden ihn dann, um das kleinste gemeinsame Vielfache zu finden.
-
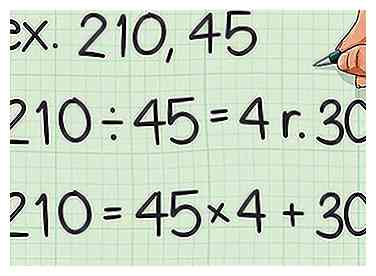 3 Verwenden Sie die größere der beiden Zahlen als Dividende. Verwenden Sie die kleinere der beiden Zahlen als Teiler. Richten Sie für diese beiden Zahlen eine Gleichung in Quotienten-Rest-Form ein.
3 Verwenden Sie die größere der beiden Zahlen als Dividende. Verwenden Sie die kleinere der beiden Zahlen als Teiler. Richten Sie für diese beiden Zahlen eine Gleichung in Quotienten-Rest-Form ein. - Wenn Sie beispielsweise versuchen, das kleinste gemeinsame Vielfache von 210 und 45 zu finden, würden Sie berechnen .
-
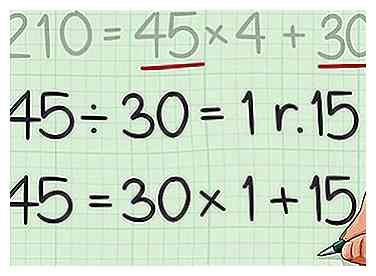 4 Verwenden Sie den ursprünglichen Divisor als neue Dividende. Verwenden Sie den Rest als neuen Teiler. Richten Sie für diese beiden Zahlen eine Gleichung in Quotienten-Rest-Form ein.
4 Verwenden Sie den ursprünglichen Divisor als neue Dividende. Verwenden Sie den Rest als neuen Teiler. Richten Sie für diese beiden Zahlen eine Gleichung in Quotienten-Rest-Form ein. - Beispielsweise, .
-
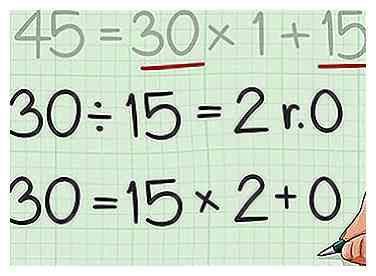 5 Wiederholen Sie diesen Vorgang, bis Sie einen Rest von 0 haben. Verwenden Sie für jede neue Gleichung den Divisor der vorherigen Gleichung als neuen Dividenden und den vorherigen Rest als neuen Divisor.[10]
5 Wiederholen Sie diesen Vorgang, bis Sie einen Rest von 0 haben. Verwenden Sie für jede neue Gleichung den Divisor der vorherigen Gleichung als neuen Dividenden und den vorherigen Rest als neuen Divisor.[10] - Beispielsweise, . Da der Rest 0 ist, brauchen Sie nicht weiter zu teilen.
-
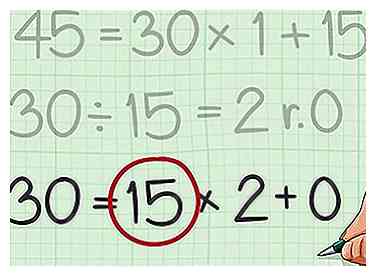 6 Schau dir den letzten Teiler an, den du benutzt hast. Dies ist der größte gemeinsame Teiler für die beiden Zahlen.[11]
6 Schau dir den letzten Teiler an, den du benutzt hast. Dies ist der größte gemeinsame Teiler für die beiden Zahlen.[11] - Zum Beispiel, da die letzte Gleichung war , der letzte Teiler war 15, und so ist 15 der größte gemeinsame Teiler von 210 und 45.
-
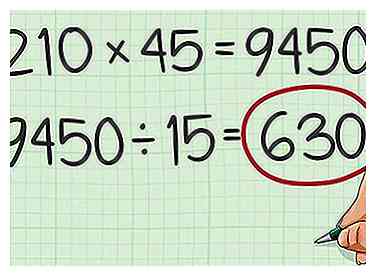 7 Multiplizieren Sie die zwei Zahlen. Teilen Sie das Produkt durch den größten gemeinsamen Teiler. Dadurch erhalten Sie das kleinste gemeinsame Vielfache der beiden Zahlen.[12]
7 Multiplizieren Sie die zwei Zahlen. Teilen Sie das Produkt durch den größten gemeinsamen Teiler. Dadurch erhalten Sie das kleinste gemeinsame Vielfache der beiden Zahlen.[12] - Beispielsweise, . Teilen durch den größten gemeinsamen Teiler, erhalten Sie . Also ist 630 das kleinste gemeinsame Vielfache von 210 und 45.
 Minotauromaquia
Minotauromaquia
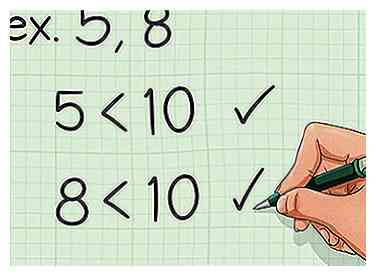 1 Bewerte deine Zahlen. Diese Methode funktioniert am besten, wenn Sie mit zwei Zahlen arbeiten, die kleiner als 10 sind. Wenn Sie mit größeren Zahlen arbeiten, empfiehlt es sich, eine andere Methode zu verwenden.
1 Bewerte deine Zahlen. Diese Methode funktioniert am besten, wenn Sie mit zwei Zahlen arbeiten, die kleiner als 10 sind. Wenn Sie mit größeren Zahlen arbeiten, empfiehlt es sich, eine andere Methode zu verwenden.  2 Schreiben Sie die ersten mehreren Vielfachen der ersten Zahl aus. Ein Vielfaches ist ein Produkt einer beliebigen Zahl und einer ganzen Zahl.[1] Mit anderen Worten, sie sind die Zahlen, die Sie in einer Multiplikationstabelle sehen würden.
2 Schreiben Sie die ersten mehreren Vielfachen der ersten Zahl aus. Ein Vielfaches ist ein Produkt einer beliebigen Zahl und einer ganzen Zahl.[1] Mit anderen Worten, sie sind die Zahlen, die Sie in einer Multiplikationstabelle sehen würden.  3 Schreibe die ersten paar Vielfachen der zweiten Zahl aus. Tun Sie dies in der Nähe der ersten Menge von Vielfachen, so dass sie leicht zu vergleichen sind.
3 Schreibe die ersten paar Vielfachen der zweiten Zahl aus. Tun Sie dies in der Nähe der ersten Menge von Vielfachen, so dass sie leicht zu vergleichen sind.  4 Finde das kleinste Vielfache, das die Zahlen gemeinsam haben. Möglicherweise müssen Sie Ihre Liste der Vielfachen erweitern, bis Sie eine der beiden Nummern finden. Diese Nummer ist Ihr am wenigsten gewöhnliches Vielfaches.[2]
4 Finde das kleinste Vielfache, das die Zahlen gemeinsam haben. Möglicherweise müssen Sie Ihre Liste der Vielfachen erweitern, bis Sie eine der beiden Nummern finden. Diese Nummer ist Ihr am wenigsten gewöhnliches Vielfaches.[2] 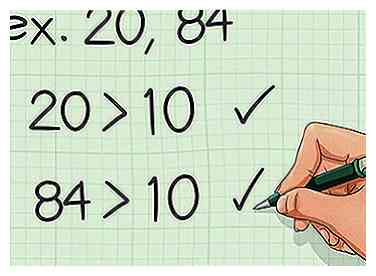 1 Bewerte deine Zahlen. Diese Methode funktioniert am besten, wenn beide Zahlen, mit denen Sie arbeiten, größer als 10 sind. Wenn Sie kleinere Zahlen haben, können Sie eine andere Methode verwenden, um das am wenigsten häufige Vielfache schneller zu finden.
1 Bewerte deine Zahlen. Diese Methode funktioniert am besten, wenn beide Zahlen, mit denen Sie arbeiten, größer als 10 sind. Wenn Sie kleinere Zahlen haben, können Sie eine andere Methode verwenden, um das am wenigsten häufige Vielfache schneller zu finden. 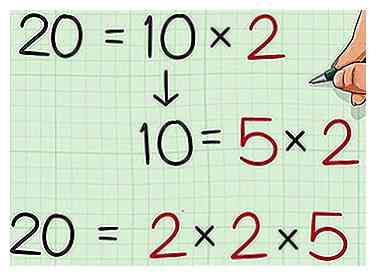 2 Faktor die erste Zahl. Sie möchten die Zahl in ihre Primfaktoren einteilen; Finde die Primfaktoren, die du multiplizieren kannst, um diese Zahl zu erhalten. Eine Möglichkeit besteht darin, einen Faktorenbaum zu erstellen. Sobald Sie mit dem Faktorisieren fertig sind, schreiben Sie die Primfaktoren als Gleichung neu.
2 Faktor die erste Zahl. Sie möchten die Zahl in ihre Primfaktoren einteilen; Finde die Primfaktoren, die du multiplizieren kannst, um diese Zahl zu erhalten. Eine Möglichkeit besteht darin, einen Faktorenbaum zu erstellen. Sobald Sie mit dem Faktorisieren fertig sind, schreiben Sie die Primfaktoren als Gleichung neu. 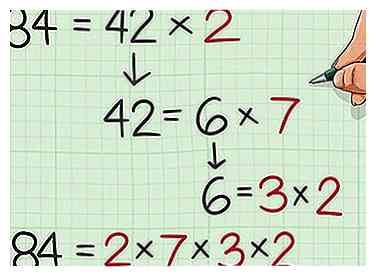 3 Faktor die zweite Zahl. Tun Sie dies auf die gleiche Weise, wie Sie die erste Zahl berechnet haben, indem Sie die Primfaktoren finden, die Sie zusammen multiplizieren können, um die Zahl zu erhalten.
3 Faktor die zweite Zahl. Tun Sie dies auf die gleiche Weise, wie Sie die erste Zahl berechnet haben, indem Sie die Primfaktoren finden, die Sie zusammen multiplizieren können, um die Zahl zu erhalten. 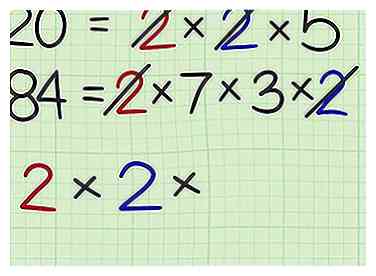 4 Notieren Sie die Faktoren für jede Anzahl Aktien. Schreiben Sie die Faktoren als Multiplikationssatz. Wenn Sie jeden Faktor schreiben, kreuzen Sie ihn in jeder Zahlenfaktorisierungsgleichung an.
4 Notieren Sie die Faktoren für jede Anzahl Aktien. Schreiben Sie die Faktoren als Multiplikationssatz. Wenn Sie jeden Faktor schreiben, kreuzen Sie ihn in jeder Zahlenfaktorisierungsgleichung an. 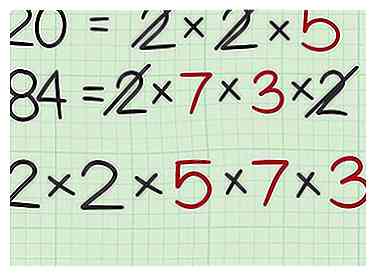 5 Fügen Sie dem Multiplikationssatz alle übrig gebliebenen Faktoren hinzu. Dies sind die Faktoren, die Sie beim Vergleich der beiden Gruppen von Faktoren nicht durchkreuzt haben. Dies sind also Faktoren, die die beiden Zahlen nicht teilen.[3]
5 Fügen Sie dem Multiplikationssatz alle übrig gebliebenen Faktoren hinzu. Dies sind die Faktoren, die Sie beim Vergleich der beiden Gruppen von Faktoren nicht durchkreuzt haben. Dies sind also Faktoren, die die beiden Zahlen nicht teilen.[3] 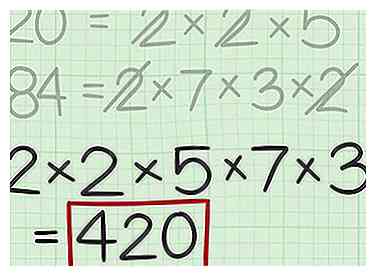 6 Berechnen Sie das kleinste gemeinsame Vielfache. Multiplizieren Sie dazu alle Faktoren in Ihrem Multiplikationssatz.
6 Berechnen Sie das kleinste gemeinsame Vielfache. Multiplizieren Sie dazu alle Faktoren in Ihrem Multiplikationssatz.  1 Zeichnen Sie ein Tic-Tac-Toe-Raster. Ein Tic-Tac-Toe-Gitter besteht aus zwei parallelen Linien, die sich senkrecht schneiden. Die Zeilen bilden drei Zeilen und drei Spalten und sehen aus wie die Rautetaste (#) auf einem Telefon oder einer Tastatur. Schreiben Sie Ihre erste Zahl in das oberste Quadrat des Gitters. Schreibe deine zweite Zahl in das obere rechte Feld des Rasters.[4]
1 Zeichnen Sie ein Tic-Tac-Toe-Raster. Ein Tic-Tac-Toe-Gitter besteht aus zwei parallelen Linien, die sich senkrecht schneiden. Die Zeilen bilden drei Zeilen und drei Spalten und sehen aus wie die Rautetaste (#) auf einem Telefon oder einer Tastatur. Schreiben Sie Ihre erste Zahl in das oberste Quadrat des Gitters. Schreibe deine zweite Zahl in das obere rechte Feld des Rasters.[4]  2 Suchen Sie nach einem Faktor, der beiden Zahlen gemeinsam ist. Schreiben Sie diese Zahl in das obere linke Quadrat Ihres Rasters. Es ist hilfreich, Primfaktoren zu verwenden, aber das muss nicht unbedingt sein.
2 Suchen Sie nach einem Faktor, der beiden Zahlen gemeinsam ist. Schreiben Sie diese Zahl in das obere linke Quadrat Ihres Rasters. Es ist hilfreich, Primfaktoren zu verwenden, aber das muss nicht unbedingt sein.  3 Unterteilen Sie den Faktor in jede Zahl. Schreibe den Quotienten in das Quadrat unter jeder Zahl. Ein Quotient ist die Antwort auf ein Teilungsproblem.
3 Unterteilen Sie den Faktor in jede Zahl. Schreibe den Quotienten in das Quadrat unter jeder Zahl. Ein Quotient ist die Antwort auf ein Teilungsproblem.  4 Finden Sie einen Faktor, der den beiden Quotienten gemeinsam ist. Wenn für beide Quotienten kein Faktor vorhanden ist, können Sie diesen und den nächsten Schritt überspringen. Wenn es einen gemeinsamen Faktor gibt, schreibe es in das mittlere linke Quadrat des Rasters.
4 Finden Sie einen Faktor, der den beiden Quotienten gemeinsam ist. Wenn für beide Quotienten kein Faktor vorhanden ist, können Sie diesen und den nächsten Schritt überspringen. Wenn es einen gemeinsamen Faktor gibt, schreibe es in das mittlere linke Quadrat des Rasters.  5 Teilen Sie diesen neuen Faktor in jeden Quotienten ein. Schreiben Sie diesen neuen Quotienten unter die ersten.
5 Teilen Sie diesen neuen Faktor in jeden Quotienten ein. Schreiben Sie diesen neuen Quotienten unter die ersten.  6 Erweitern Sie bei Bedarf Ihr Raster. Folgen Sie diesem Vorgang, bis Sie einen Punkt erreicht haben, an dem die letzten Quotienten keinen gemeinsamen Faktor haben.
6 Erweitern Sie bei Bedarf Ihr Raster. Folgen Sie diesem Vorgang, bis Sie einen Punkt erreicht haben, an dem die letzten Quotienten keinen gemeinsamen Faktor haben.  7 Zeichnen Sie einen Kreis um die Zahlen in der ersten Spalte und der letzten Zeile Ihres Rasters. Sie können sich das so vorstellen, als würden Sie ein "L" für "geringstes gemeinsames Vielfaches" zeichnen. Schreiben Sie einen Multiplikationssatz mit all diesen Faktoren.[5]
7 Zeichnen Sie einen Kreis um die Zahlen in der ersten Spalte und der letzten Zeile Ihres Rasters. Sie können sich das so vorstellen, als würden Sie ein "L" für "geringstes gemeinsames Vielfaches" zeichnen. Schreiben Sie einen Multiplikationssatz mit all diesen Faktoren.[5] 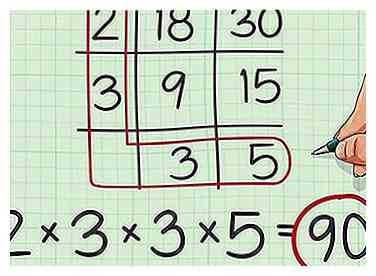 8 Beende die Multiplikation. Wenn Sie alle diese Faktoren zusammen multiplizieren, ist das Ergebnis das kleinste gemeinsame Vielfache Ihrer zwei ursprünglichen Zahlen.[6]
8 Beende die Multiplikation. Wenn Sie alle diese Faktoren zusammen multiplizieren, ist das Ergebnis das kleinste gemeinsame Vielfache Ihrer zwei ursprünglichen Zahlen.[6]  1 Verstehe das Vokabular der Teilung. Die Dividende ist die Nummer, die geteilt wird. Der Divisor ist die Zahl, um die die Dividende geteilt wird. Der Quotient ist die Antwort auf das Teilungsproblem. Der Rest ist der Betrag, der übrig bleibt, nachdem eine Zahl durch eine andere geteilt wurde.[7]
1 Verstehe das Vokabular der Teilung. Die Dividende ist die Nummer, die geteilt wird. Der Divisor ist die Zahl, um die die Dividende geteilt wird. Der Quotient ist die Antwort auf das Teilungsproblem. Der Rest ist der Betrag, der übrig bleibt, nachdem eine Zahl durch eine andere geteilt wurde.[7] 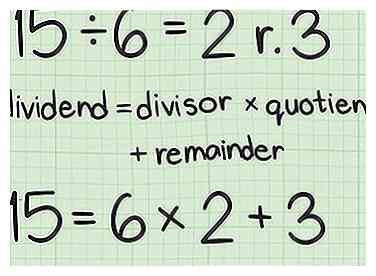 2 Richten Sie die Formel für die Quotienten-Rest-Form ein. Die Formel ist
2 Richten Sie die Formel für die Quotienten-Rest-Form ein. Die Formel ist 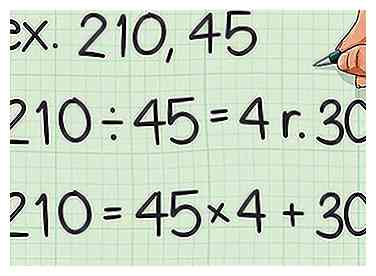 3 Verwenden Sie die größere der beiden Zahlen als Dividende. Verwenden Sie die kleinere der beiden Zahlen als Teiler. Richten Sie für diese beiden Zahlen eine Gleichung in Quotienten-Rest-Form ein.
3 Verwenden Sie die größere der beiden Zahlen als Dividende. Verwenden Sie die kleinere der beiden Zahlen als Teiler. Richten Sie für diese beiden Zahlen eine Gleichung in Quotienten-Rest-Form ein. 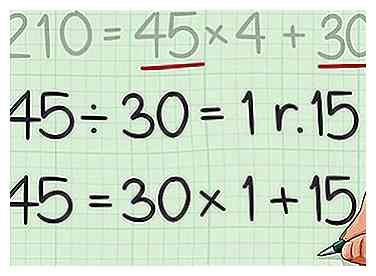 4 Verwenden Sie den ursprünglichen Divisor als neue Dividende. Verwenden Sie den Rest als neuen Teiler. Richten Sie für diese beiden Zahlen eine Gleichung in Quotienten-Rest-Form ein.
4 Verwenden Sie den ursprünglichen Divisor als neue Dividende. Verwenden Sie den Rest als neuen Teiler. Richten Sie für diese beiden Zahlen eine Gleichung in Quotienten-Rest-Form ein. 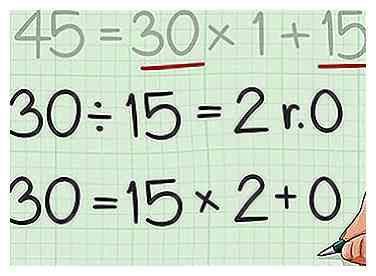 5 Wiederholen Sie diesen Vorgang, bis Sie einen Rest von 0 haben. Verwenden Sie für jede neue Gleichung den Divisor der vorherigen Gleichung als neuen Dividenden und den vorherigen Rest als neuen Divisor.[10]
5 Wiederholen Sie diesen Vorgang, bis Sie einen Rest von 0 haben. Verwenden Sie für jede neue Gleichung den Divisor der vorherigen Gleichung als neuen Dividenden und den vorherigen Rest als neuen Divisor.[10] 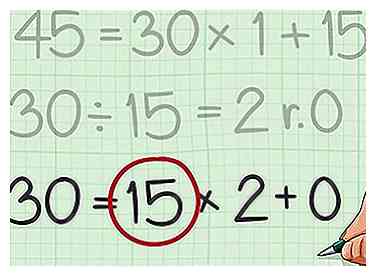 6 Schau dir den letzten Teiler an, den du benutzt hast. Dies ist der größte gemeinsame Teiler für die beiden Zahlen.[11]
6 Schau dir den letzten Teiler an, den du benutzt hast. Dies ist der größte gemeinsame Teiler für die beiden Zahlen.[11] 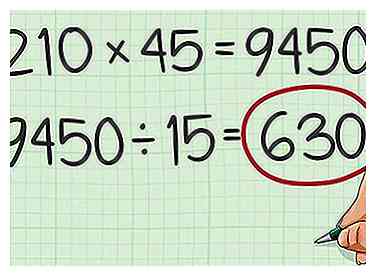 7 Multiplizieren Sie die zwei Zahlen. Teilen Sie das Produkt durch den größten gemeinsamen Teiler. Dadurch erhalten Sie das kleinste gemeinsame Vielfache der beiden Zahlen.[12]
7 Multiplizieren Sie die zwei Zahlen. Teilen Sie das Produkt durch den größten gemeinsamen Teiler. Dadurch erhalten Sie das kleinste gemeinsame Vielfache der beiden Zahlen.[12]