Wenn zwei Variablen direkt proportional sind, ändern sie sich mit der gleichen Rate. Die Rate wird durch die Konstante angezeigt in der Gleichung . Direktproportionale Größen werden graphisch durch eine gerade Linie angezeigt, die durch den Ursprung der Koordinatenebene verläuft. Sobald Sie diese grundlegenden Konzepte verstanden haben, ist es einfach, direkt proportionale Variablen zu identifizieren, indem Sie die Gleichung ihrer Linie oder ihre Werte verwenden.
Methode eins von vier:
Die Gleichung der Linie umschreiben
-
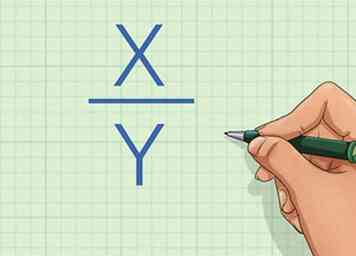 1 Verstehen Sie die direkte Proportion. Zwei Variablen sind direkt proportional, wenn sich jede Variable mit der gleichen Rate ändert.[1] Mit anderen Worten, wenn Änderungen um einen bestimmten Faktor oder eine Konstante (), dann ändert sich um dieselbe Konstante ().
1 Verstehen Sie die direkte Proportion. Zwei Variablen sind direkt proportional, wenn sich jede Variable mit der gleichen Rate ändert.[1] Mit anderen Worten, wenn Änderungen um einen bestimmten Faktor oder eine Konstante (), dann ändert sich um dieselbe Konstante (). -
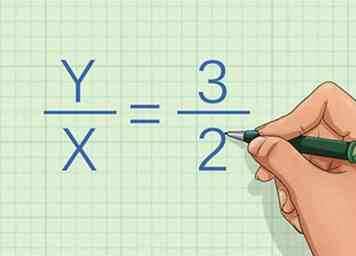 2 Schreiben Sie die Gleichung der Linie auf. Die Gleichung wird zwei Variablen und eine Konstante haben. Wenn Sie die Gleichung nicht erhalten, können Sie diese Methode nicht verwenden.
2 Schreiben Sie die Gleichung der Linie auf. Die Gleichung wird zwei Variablen und eine Konstante haben. Wenn Sie die Gleichung nicht erhalten, können Sie diese Methode nicht verwenden. - Zum Beispiel könnten Sie die Gleichung erhalten .
-
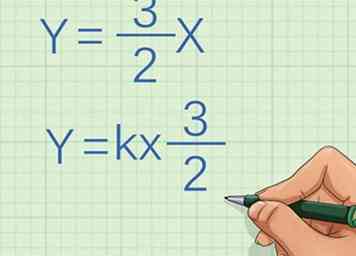 3 Schreiben Sie die Gleichung in Form der direkten Proportion oder Variation neu. Die Gleichung ist , woher entspricht der Y-Koordinate eines Punktes auf der Linie, entspricht der x-Koordinate für denselben Punkt und ist die Konstante oder Steigung der Linie. Verwenden Sie Algebra, um die Gleichung in Form von neu zu ordnen . Wenn Sie die Gleichung in dieser Form nicht umschreiben können, sind die Variablen nicht direkt proportional. Wenn Sie können, beweist es, dass sie direkt proportional sind.[2]
3 Schreiben Sie die Gleichung in Form der direkten Proportion oder Variation neu. Die Gleichung ist , woher entspricht der Y-Koordinate eines Punktes auf der Linie, entspricht der x-Koordinate für denselben Punkt und ist die Konstante oder Steigung der Linie. Verwenden Sie Algebra, um die Gleichung in Form von neu zu ordnen . Wenn Sie die Gleichung in dieser Form nicht umschreiben können, sind die Variablen nicht direkt proportional. Wenn Sie können, beweist es, dass sie direkt proportional sind.[2] - Zum Beispiel, wenn Sie beide Seiten der Gleichung multiplizieren durch , wird die Gleichung , die in Form von ist mit die Konstante sein.
Methode zwei von vier:
Verwenden einer Reihe von Punkten
-
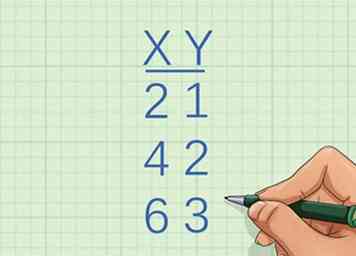 1 Identifizieren Sie die X-Koordinaten der ersten beiden Punkte. Sie sollten eine Liste von Koordinaten erhalten oder ein Diagramm haben, mit dem Sie die Koordinaten der Punkte bestimmen können. Wenn Sie nicht über die Koordinaten von Punkten in der Linie verfügen, können Sie diese Methode nicht verwenden.
1 Identifizieren Sie die X-Koordinaten der ersten beiden Punkte. Sie sollten eine Liste von Koordinaten erhalten oder ein Diagramm haben, mit dem Sie die Koordinaten der Punkte bestimmen können. Wenn Sie nicht über die Koordinaten von Punkten in der Linie verfügen, können Sie diese Methode nicht verwenden. - Zum Beispiel könnten Sie die Menge der Punkte erhalten
- Die x-Koordinate des ersten Punktes ist 2 und die x-Koordinate des zweiten Punktes ist 4.
-
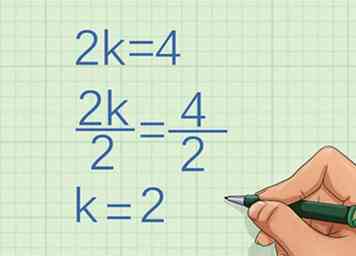 2 Bestimmen Sie den Faktor, mit dem die Variable wächst. Bestimmen Sie dazu, um welchen Faktor oder um welche Konstante die erste x-Koordinate multipliziert wird, um zur zweiten Koordinate zu gelangen.
2 Bestimmen Sie den Faktor, mit dem die Variable wächst. Bestimmen Sie dazu, um welchen Faktor oder um welche Konstante die erste x-Koordinate multipliziert wird, um zur zweiten Koordinate zu gelangen. - Wenn beispielsweise die erste x-Koordinate 2 ist und die zweite x-Koordinate 4 ist, müssen Sie bestimmen, wie Sie 2 multiplizieren, um 4 zu erhalten:
Also, die Variable wächst um die Konstante 2.
- Wenn beispielsweise die erste x-Koordinate 2 ist und die zweite x-Koordinate 4 ist, müssen Sie bestimmen, wie Sie 2 multiplizieren, um 4 zu erhalten:
-
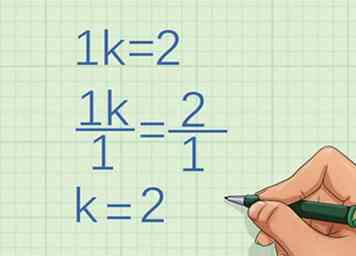 3 Bestimmen Sie den Faktor, mit dem die Variable wächst. Verwenden Sie die gleichen zwei Punkte, die Sie verwendet haben, um das Wachstum von zu bestimmen . Verwenden Sie Algebra, um den Faktor zu bestimmen, um den die zwei Koordinaten variieren.
3 Bestimmen Sie den Faktor, mit dem die Variable wächst. Verwenden Sie die gleichen zwei Punkte, die Sie verwendet haben, um das Wachstum von zu bestimmen . Verwenden Sie Algebra, um den Faktor zu bestimmen, um den die zwei Koordinaten variieren. - Wenn zum Beispiel die erste y-Koordinate 1 ist und die zweite y-Koordinate 2 ist, müssen Sie bestimmen, wie Sie 1 multiplizieren, um 2 zu erhalten:
Also, die Variable wächst um die Konstante 2.
- Wenn zum Beispiel die erste y-Koordinate 1 ist und die zweite y-Koordinate 2 ist, müssen Sie bestimmen, wie Sie 1 multiplizieren, um 2 zu erhalten:
-
 4 Vergleichen Sie die Konstanten der beiden Variablen. Ob und mit der gleichen Rate oder um den gleichen Faktor geändert, dann sind sie direkt proportional.[3]
4 Vergleichen Sie die Konstanten der beiden Variablen. Ob und mit der gleichen Rate oder um den gleichen Faktor geändert, dann sind sie direkt proportional.[3] - Da sich beispielsweise die x-Koordinaten um einen Faktor 2 geändert haben, während sich die y-Koordinaten ebenfalls um einen Faktor 2 geändert haben, sind die beiden Variablen direkt proportional.
Methode drei von vier:
Verwenden eines Diagramms
-
 1 Beachten Sie, ob die Linie gerade ist. Wenn zwei Variablen proportional sind, ist die Linie, die sie darstellt, gerade.[4] Dies bedeutet, dass die Steigung der Linie konstant ist oder der Gleichung folgt .
1 Beachten Sie, ob die Linie gerade ist. Wenn zwei Variablen proportional sind, ist die Linie, die sie darstellt, gerade.[4] Dies bedeutet, dass die Steigung der Linie konstant ist oder der Gleichung folgt . -
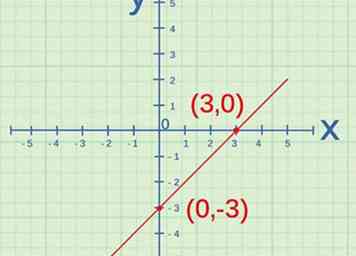 2 Bestimme den y-Achsenabschnitt. Der y-Achsenabschnitt ist der Punkt, an dem die Linie die y-Achse kreuzt. Wenn zwei Variablen direkt proportional sind, durchläuft ihre Linie beim Graphen den Ursprung. Der Ursprung ist an dem Punkt Also sollte der y-Schnittpunkt der Linie sein . Wenn dies nicht der Fall ist, sind die Variablen nicht direkt proportional.[5]
2 Bestimme den y-Achsenabschnitt. Der y-Achsenabschnitt ist der Punkt, an dem die Linie die y-Achse kreuzt. Wenn zwei Variablen direkt proportional sind, durchläuft ihre Linie beim Graphen den Ursprung. Der Ursprung ist an dem Punkt Also sollte der y-Schnittpunkt der Linie sein . Wenn dies nicht der Fall ist, sind die Variablen nicht direkt proportional.[5] - Die y-Achse ist die vertikale Achse.
-
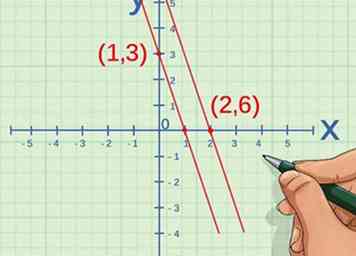 3 Finde die Koordinaten von zwei Punkten auf der Linie. Vergleichen Sie die Koordinaten miteinander und bestimmen Sie, ob sich jede Koordinate um denselben Faktor ändert.[6] Das heißt, bestimmen, ob die Konstante () ist das gleiche für beide und Werte.
3 Finde die Koordinaten von zwei Punkten auf der Linie. Vergleichen Sie die Koordinaten miteinander und bestimmen Sie, ob sich jede Koordinate um denselben Faktor ändert.[6] Das heißt, bestimmen, ob die Konstante () ist das gleiche für beide und Werte. - Zum Beispiel, wenn der erste Punkt ist und der zweite Punkt ist , die x-Koordinate um den Faktor 2 verändert, da . Auch die y-Koordinate hat sich um den Faktor 2 verändert . So können Sie bestätigen, dass die Linie zwei Variablen darstellt, die direkt proportional sind.
Methode vier von vier:
Abschließen von Beispielproblemen
-
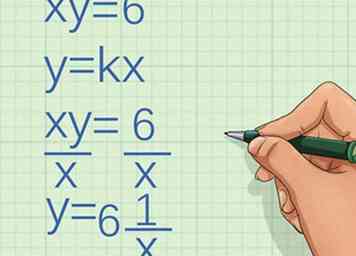 1 Schau dir die Gleichung an. Bestimmen Sie, ob die beiden Variablen direkt proportional sind: .
1 Schau dir die Gleichung an. Bestimmen Sie, ob die beiden Variablen direkt proportional sind: . - Denken Sie daran, dass die Variablen, wenn sie direkt proportional sind, dem Muster folgen .
- Verwenden Sie Algebra, um die Gleichung neu zu schreiben.
- Isolieren Sie die Variable durch Teilen jeder Seite durch :
- Isolieren Sie die Variable durch Teilen jeder Seite durch :
- Beurteilen Sie, ob die neu geschriebene Gleichung dem Muster folgt . In diesem Fall ist die Gleichung nicht, also sind die Variablen nicht direkt proportional. In der Tat sind sie umgekehrt proportional.[7]
-
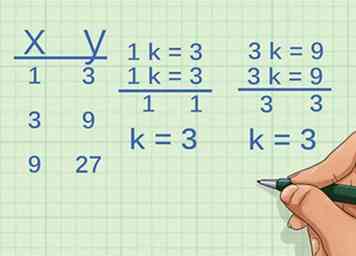 2 Betrachten Sie die folgenden Punkte. Sind die Variablen direkt proportional?
2 Betrachten Sie die folgenden Punkte. Sind die Variablen direkt proportional?
- Bestimmen Sie das Wachstum von . Tun Sie dies, indem Sie den Faktor finden, mit dem Sie die erste x-Koordinate multiplizieren, um die zweite Koordinate zu erreichen:
Die x-Koordinate wächst also um den Faktor 3. - Bestimmen Sie das Wachstum von :
So wächst die y-Koordinate um den Faktor 3. - Vergleichen Sie den Faktor oder die Konstante der beiden Variablen. Sie wachsen beide um den Faktor 3. Daher sind die Variablen direkt proportional.
- Bestimmen Sie das Wachstum von . Tun Sie dies, indem Sie den Faktor finden, mit dem Sie die erste x-Koordinate multiplizieren, um die zweite Koordinate zu erreichen:
-
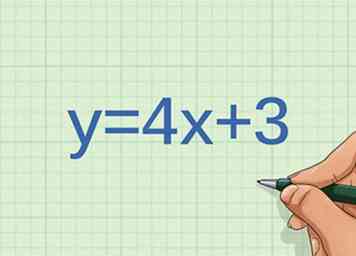 3 Betrachten Sie ein Diagramm der Linie . Zeigt das Diagramm direkte Proportionen zwischen Variablen?
3 Betrachten Sie ein Diagramm der Linie . Zeigt das Diagramm direkte Proportionen zwischen Variablen? - Beachten Sie, ob die Linie gerade ist. Da die Gleichung der Linie in der Steigung abgefangen wird, hat sie eine konstante Steigung, was bedeutet, dass die Linie gerade ist. Die Variablen sind also möglicherweise direkt proportional.
- Bestimme den y-Achsenabschnitt. Wenn die Variablen direkt proportional sind, wird die Linie durch den Punkt gehen . Der y-Achsenabschnitt dieser Linie ist der Punkt . Also sind die Variablen nicht direkt proportional.
 Minotauromaquia
Minotauromaquia
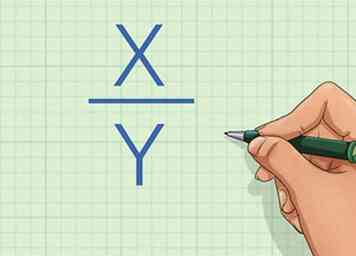 1 Verstehen Sie die direkte Proportion. Zwei Variablen sind direkt proportional, wenn sich jede Variable mit der gleichen Rate ändert.[1] Mit anderen Worten, wenn
1 Verstehen Sie die direkte Proportion. Zwei Variablen sind direkt proportional, wenn sich jede Variable mit der gleichen Rate ändert.[1] Mit anderen Worten, wenn 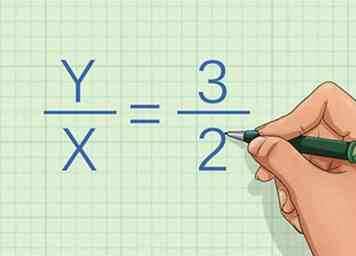 2 Schreiben Sie die Gleichung der Linie auf. Die Gleichung wird zwei Variablen und eine Konstante haben. Wenn Sie die Gleichung nicht erhalten, können Sie diese Methode nicht verwenden.
2 Schreiben Sie die Gleichung der Linie auf. Die Gleichung wird zwei Variablen und eine Konstante haben. Wenn Sie die Gleichung nicht erhalten, können Sie diese Methode nicht verwenden. 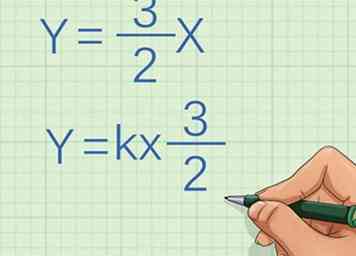 3 Schreiben Sie die Gleichung in Form der direkten Proportion oder Variation neu. Die Gleichung ist
3 Schreiben Sie die Gleichung in Form der direkten Proportion oder Variation neu. Die Gleichung ist  1 Identifizieren Sie die X-Koordinaten der ersten beiden Punkte. Sie sollten eine Liste von Koordinaten erhalten oder ein Diagramm haben, mit dem Sie die Koordinaten der Punkte bestimmen können. Wenn Sie nicht über die Koordinaten von Punkten in der Linie verfügen, können Sie diese Methode nicht verwenden.
1 Identifizieren Sie die X-Koordinaten der ersten beiden Punkte. Sie sollten eine Liste von Koordinaten erhalten oder ein Diagramm haben, mit dem Sie die Koordinaten der Punkte bestimmen können. Wenn Sie nicht über die Koordinaten von Punkten in der Linie verfügen, können Sie diese Methode nicht verwenden. 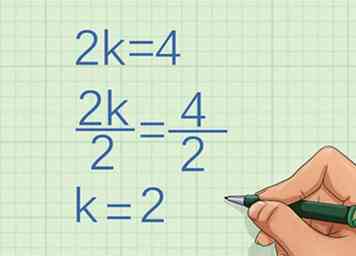 2 Bestimmen Sie den Faktor, mit dem die
2 Bestimmen Sie den Faktor, mit dem die 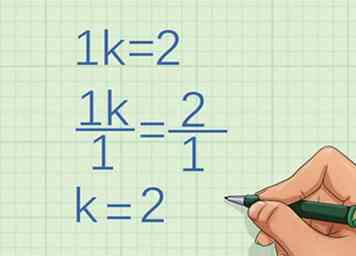 3 Bestimmen Sie den Faktor, mit dem die
3 Bestimmen Sie den Faktor, mit dem die  4 Vergleichen Sie die Konstanten der beiden Variablen. Ob
4 Vergleichen Sie die Konstanten der beiden Variablen. Ob  1 Beachten Sie, ob die Linie gerade ist. Wenn zwei Variablen proportional sind, ist die Linie, die sie darstellt, gerade.[4] Dies bedeutet, dass die Steigung der Linie konstant ist oder der Gleichung folgt
1 Beachten Sie, ob die Linie gerade ist. Wenn zwei Variablen proportional sind, ist die Linie, die sie darstellt, gerade.[4] Dies bedeutet, dass die Steigung der Linie konstant ist oder der Gleichung folgt  2 Bestimme den y-Achsenabschnitt. Der y-Achsenabschnitt ist der Punkt, an dem die Linie die y-Achse kreuzt. Wenn zwei Variablen direkt proportional sind, durchläuft ihre Linie beim Graphen den Ursprung. Der Ursprung ist an dem Punkt
2 Bestimme den y-Achsenabschnitt. Der y-Achsenabschnitt ist der Punkt, an dem die Linie die y-Achse kreuzt. Wenn zwei Variablen direkt proportional sind, durchläuft ihre Linie beim Graphen den Ursprung. Der Ursprung ist an dem Punkt  3 Finde die Koordinaten von zwei Punkten auf der Linie. Vergleichen Sie die Koordinaten miteinander und bestimmen Sie, ob sich jede Koordinate um denselben Faktor ändert.[6] Das heißt, bestimmen, ob die Konstante (
3 Finde die Koordinaten von zwei Punkten auf der Linie. Vergleichen Sie die Koordinaten miteinander und bestimmen Sie, ob sich jede Koordinate um denselben Faktor ändert.[6] Das heißt, bestimmen, ob die Konstante (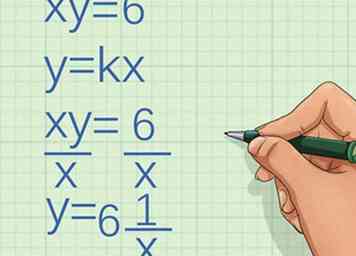 1 Schau dir die Gleichung an. Bestimmen Sie, ob die beiden Variablen direkt proportional sind:
1 Schau dir die Gleichung an. Bestimmen Sie, ob die beiden Variablen direkt proportional sind: 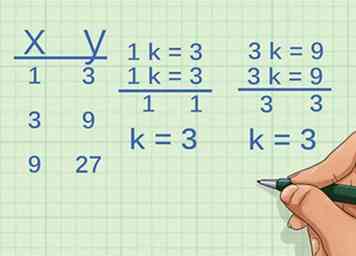 2 Betrachten Sie die folgenden Punkte. Sind die Variablen direkt proportional?
2 Betrachten Sie die folgenden Punkte. Sind die Variablen direkt proportional?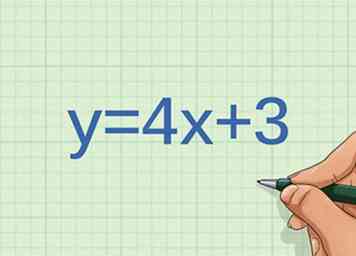 3 Betrachten Sie ein Diagramm der Linie
3 Betrachten Sie ein Diagramm der Linie