Der Bereich einer Funktion ist die Menge der Zahlen, die die Funktion erzeugen kann. Mit anderen Worten, es ist die Menge der y-Werte, die Sie erhalten, wenn Sie alle möglichen x-Werte in die Funktion einklinken. Diese Menge möglicher x-Werte wird als Domäne bezeichnet. Wenn Sie wissen möchten, wie Sie den Bereich einer Funktion finden, folgen Sie einfach diesen Schritten.
Methode eins von vier:
Den Bereich einer Funktion anhand einer Formel finden
-
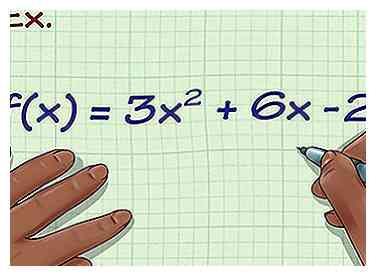 1 Schreiben Sie die Formel auf. Nehmen wir an, die Formel, mit der Sie arbeiten, lautet wie folgt: f (x) = 3x2 + 6x -2. Dies bedeutet, dass wenn Sie einen platzieren x in die Gleichung bekommen Sie Ihre y Wert. Dies ist die Funktion einer Parabel.
1 Schreiben Sie die Formel auf. Nehmen wir an, die Formel, mit der Sie arbeiten, lautet wie folgt: f (x) = 3x2 + 6x -2. Dies bedeutet, dass wenn Sie einen platzieren x in die Gleichung bekommen Sie Ihre y Wert. Dies ist die Funktion einer Parabel. -
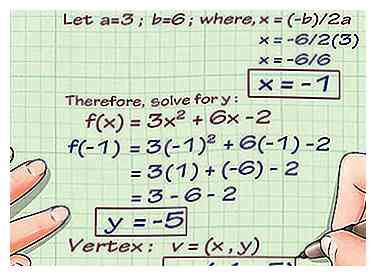 2 Suchen Sie den Eckpunkt der Funktion, wenn sie quadratisch ist. Wenn Sie mit einer geraden Linie oder einer Funktion mit einem Polynom einer ungeraden Zahl arbeiten, z. B. f (x) = 6x3+ 2x + 7, können Sie diesen Schritt überspringen. Aber wenn Sie mit einer Parabel oder einer Gleichung arbeiten, bei der die x-Koordinate quadriert oder auf eine gerade Potenz erhöht wird, müssen Sie den Scheitelpunkt plotten. Verwenden Sie dazu einfach die Formel -b / 2a um die x-Koordinate der Funktion 3x zu erhalten2 + 6x -2, wobei 3 = a, 6 = b und -2 = c. In diesem Fall -b ist -6 und 2a ist 6, also ist die x-Koordinate -6/6 oder -1.
2 Suchen Sie den Eckpunkt der Funktion, wenn sie quadratisch ist. Wenn Sie mit einer geraden Linie oder einer Funktion mit einem Polynom einer ungeraden Zahl arbeiten, z. B. f (x) = 6x3+ 2x + 7, können Sie diesen Schritt überspringen. Aber wenn Sie mit einer Parabel oder einer Gleichung arbeiten, bei der die x-Koordinate quadriert oder auf eine gerade Potenz erhöht wird, müssen Sie den Scheitelpunkt plotten. Verwenden Sie dazu einfach die Formel -b / 2a um die x-Koordinate der Funktion 3x zu erhalten2 + 6x -2, wobei 3 = a, 6 = b und -2 = c. In diesem Fall -b ist -6 und 2a ist 6, also ist die x-Koordinate -6/6 oder -1. - Stecken Sie nun -1 in die Funktion, um die y-Koordinate zu erhalten. f (-1) = 3 (-1)2 + 6(-1) -2 = 3 - 6 -2 = -5.
- Der Vertex ist (-1, -5). Zeichnen Sie einen Punkt, an dem die x-Koordinate -1 ist und die y-Koordinate -5 ist. Es sollte im dritten Quadranten der Grafik sein.
-
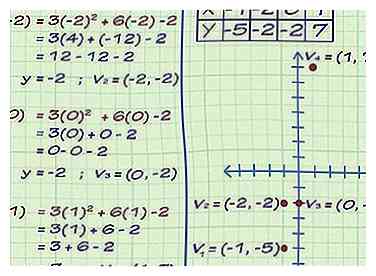 3 Finde ein paar andere Punkte in der Funktion. Um ein Gefühl für die Funktion zu bekommen, sollten Sie ein paar andere x-Koordinaten einstecken, damit Sie einen Eindruck davon bekommen, wie die Funktion aussieht, bevor Sie nach dem Bereich suchen. Da ist es eine Parabel und das x2 Koordinate ist positiv, es wird nach oben zeigen. Aber um Ihre Basen zu bedecken, lassen Sie uns einige x-Koordinaten einstecken, um zu sehen, welche y-Koordinaten sie liefern:
3 Finde ein paar andere Punkte in der Funktion. Um ein Gefühl für die Funktion zu bekommen, sollten Sie ein paar andere x-Koordinaten einstecken, damit Sie einen Eindruck davon bekommen, wie die Funktion aussieht, bevor Sie nach dem Bereich suchen. Da ist es eine Parabel und das x2 Koordinate ist positiv, es wird nach oben zeigen. Aber um Ihre Basen zu bedecken, lassen Sie uns einige x-Koordinaten einstecken, um zu sehen, welche y-Koordinaten sie liefern: - f (-2) = 3 (-2)2 + 6 (-2) -2 = -2. Ein Punkt in der Grafik ist (-2, -2)
- f (0) = 3 (0)2 + 6 (0) -2 = -2. Ein weiterer Punkt in der Grafik ist (0, -2)
- f (1) = 3 (1)2 + 6 (1) -2 = 7. Ein dritter Punkt in der Grafik ist (1, 7).
-
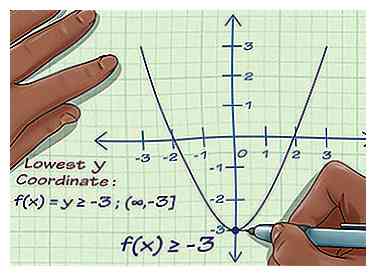
 4 Finde den Bereich in der Grafik. Betrachten Sie nun die y-Koordinaten in der Grafik und finden Sie den tiefsten Punkt, an dem der Graph eine y-Koordinate berührt. In diesem Fall befindet sich die niedrigste y-Koordinate am Scheitelpunkt -5, und der Graph erstreckt sich unendlich über diesen Punkt. Dies bedeutet, dass der Bereich der Funktion ist y = alle reellen Zahlen ≥ -5.
4 Finde den Bereich in der Grafik. Betrachten Sie nun die y-Koordinaten in der Grafik und finden Sie den tiefsten Punkt, an dem der Graph eine y-Koordinate berührt. In diesem Fall befindet sich die niedrigste y-Koordinate am Scheitelpunkt -5, und der Graph erstreckt sich unendlich über diesen Punkt. Dies bedeutet, dass der Bereich der Funktion ist y = alle reellen Zahlen ≥ -5.
Methode zwei von vier:
Den Bereich einer Funktion in einem Diagramm finden
-
 1 Finde das Minimum der Funktion. Suchen Sie nach der niedrigsten Y-Koordinate der Funktion. Nehmen wir an, die Funktion erreicht ihren niedrigsten Punkt bei -3. Diese Funktion könnte auch unendlich kleiner werden, so dass sie keinen tiefsten Punkt hat - nur unendlich.
1 Finde das Minimum der Funktion. Suchen Sie nach der niedrigsten Y-Koordinate der Funktion. Nehmen wir an, die Funktion erreicht ihren niedrigsten Punkt bei -3. Diese Funktion könnte auch unendlich kleiner werden, so dass sie keinen tiefsten Punkt hat - nur unendlich. -
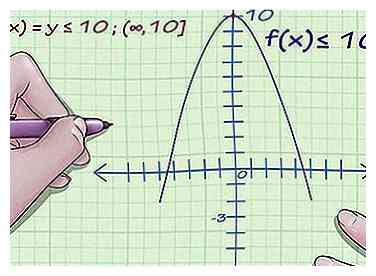 2 Finde das Maximum der Funktion. Nehmen wir an, die höchste y-Koordinate, die die Funktion erreicht, ist 10. Diese Funktion könnte auch unendlich größer werden, also hat sie keinen höchsten Punkt - nur unendlich.
2 Finde das Maximum der Funktion. Nehmen wir an, die höchste y-Koordinate, die die Funktion erreicht, ist 10. Diese Funktion könnte auch unendlich größer werden, also hat sie keinen höchsten Punkt - nur unendlich. -
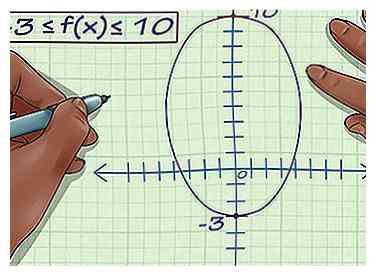 3 Geben Sie den Bereich an. Dies bedeutet, dass der Bereich der Funktion oder der Bereich der y-Koordinaten von -3 bis 10 reicht. Also, -3 ≤ f (x) ≤ 10. Das ist der Bereich der Funktion.
3 Geben Sie den Bereich an. Dies bedeutet, dass der Bereich der Funktion oder der Bereich der y-Koordinaten von -3 bis 10 reicht. Also, -3 ≤ f (x) ≤ 10. Das ist der Bereich der Funktion. - Nehmen wir an, der Graph erreicht seinen tiefsten Punkt bei y = -3, geht aber für immer nach oben. Dann ist der Bereich f (x) ≥ -3 und das ist es.
- Nehmen wir an, der Graph erreicht seinen höchsten Punkt bei 10, geht aber für immer nach unten. Dann ist der Bereich f (x) ≤ 10.
Methode drei von vier:
Den Bereich einer Funktion einer Beziehung finden
-
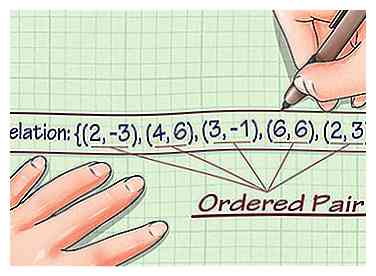 1 Schreiben Sie die Beziehung auf. Eine Relation ist eine Menge geordneter Paare mit x- und y-Koordinaten. Sie können eine Beziehung betrachten und ihre Domäne und ihren Bereich bestimmen. Nehmen wir an, Sie arbeiten mit der folgenden Beziehung: (2, -3), (4, 6), (3, -1), (6, 6), (2, 3).[1]
1 Schreiben Sie die Beziehung auf. Eine Relation ist eine Menge geordneter Paare mit x- und y-Koordinaten. Sie können eine Beziehung betrachten und ihre Domäne und ihren Bereich bestimmen. Nehmen wir an, Sie arbeiten mit der folgenden Beziehung: (2, -3), (4, 6), (3, -1), (6, 6), (2, 3).[1] -
 2 Listen Sie die y-Koordinaten der Relation auf. Um den Bereich der Beziehung zu finden, schreiben Sie einfach alle y-Koordinaten jedes geordneten Paares auf: -3, 6, -1, 6, 3.[2]
2 Listen Sie die y-Koordinaten der Relation auf. Um den Bereich der Beziehung zu finden, schreiben Sie einfach alle y-Koordinaten jedes geordneten Paares auf: -3, 6, -1, 6, 3.[2] -
 3 Entfernen Sie alle doppelten Koordinaten, so dass Sie nur eine von jeder Y-Koordinate haben. Sie werden feststellen, dass Sie zweimal "6" aufgelistet haben. Nimm es raus, so dass du -3, -1, 6, 3 übrig hast.[3]
3 Entfernen Sie alle doppelten Koordinaten, so dass Sie nur eine von jeder Y-Koordinate haben. Sie werden feststellen, dass Sie zweimal "6" aufgelistet haben. Nimm es raus, so dass du -3, -1, 6, 3 übrig hast.[3] -
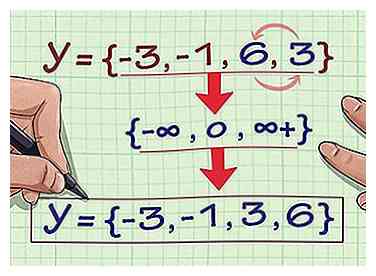 4 Schreiben Sie den Bereich der Beziehung in aufsteigender Reihenfolge. Ordnen Sie nun die Zahlen im Satz neu an, so dass Sie vom kleinsten zum größten übergehen und Ihre Reichweite haben. Der Bereich der Beziehung (2, -3), (4, 6), (3, -1), (6, 6), (2, 3) ist -3, -1, 3, 6 . Du bist fertig.[4]
4 Schreiben Sie den Bereich der Beziehung in aufsteigender Reihenfolge. Ordnen Sie nun die Zahlen im Satz neu an, so dass Sie vom kleinsten zum größten übergehen und Ihre Reichweite haben. Der Bereich der Beziehung (2, -3), (4, 6), (3, -1), (6, 6), (2, 3) ist -3, -1, 3, 6 . Du bist fertig.[4] -
 5 Stellen Sie sicher, dass die Beziehung ist eine Funktion. Damit eine Relation eine Funktion ist, muss die y-Koordinate bei jeder Eingabe einer x-Koordinate gleich sein. Zum Beispiel ist die Beziehung (2, 3) (2, 4) (6, 9) nicht eine Funktion, denn wenn du zum ersten Mal 2 als x eingibst, hast du eine 3, aber das zweite Mal, wenn du eine 2 eingibst, hast du eine Vier. Damit eine Beziehung eine Funktion ist, sollten Sie, wenn Sie dieselbe Eingabe eingeben, immer dieselbe Ausgabe erhalten. Wenn Sie eine -7 eingeben, sollten Sie jedes Mal die gleiche y-Koordinate erhalten (was auch immer es sein mag).[5]
5 Stellen Sie sicher, dass die Beziehung ist eine Funktion. Damit eine Relation eine Funktion ist, muss die y-Koordinate bei jeder Eingabe einer x-Koordinate gleich sein. Zum Beispiel ist die Beziehung (2, 3) (2, 4) (6, 9) nicht eine Funktion, denn wenn du zum ersten Mal 2 als x eingibst, hast du eine 3, aber das zweite Mal, wenn du eine 2 eingibst, hast du eine Vier. Damit eine Beziehung eine Funktion ist, sollten Sie, wenn Sie dieselbe Eingabe eingeben, immer dieselbe Ausgabe erhalten. Wenn Sie eine -7 eingeben, sollten Sie jedes Mal die gleiche y-Koordinate erhalten (was auch immer es sein mag).[5]
Methode vier von vier:
Den Bereich einer Funktion in einem Wort finden Problem
-
 1 Lesen Sie das Problem. Nehmen wir an, Sie arbeiten mit folgendem Problem: "Becky verkauft Tickets für die Talentshow ihrer Schule für jeweils 5 Dollar. Die Menge an Geld, die sie sammelt, hängt davon ab, wie viele Tickets sie verkauft. Was ist der Umfang der Funktion?"
1 Lesen Sie das Problem. Nehmen wir an, Sie arbeiten mit folgendem Problem: "Becky verkauft Tickets für die Talentshow ihrer Schule für jeweils 5 Dollar. Die Menge an Geld, die sie sammelt, hängt davon ab, wie viele Tickets sie verkauft. Was ist der Umfang der Funktion?" -
 2 Schreiben Sie das Problem als eine Funktion. In diesem Fall, M stellt den Geldbetrag dar, den sie sammelt, und t stellt die Menge an Tickets dar, die sie verkauft.Da jedoch jedes Ticket 5 Dollar kostet, müssen Sie die Menge der verkauften Tickets mit 5 multiplizieren, um den Geldbetrag zu finden. Daher kann die Funktion als geschrieben werden M (t) = 5t.
2 Schreiben Sie das Problem als eine Funktion. In diesem Fall, M stellt den Geldbetrag dar, den sie sammelt, und t stellt die Menge an Tickets dar, die sie verkauft.Da jedoch jedes Ticket 5 Dollar kostet, müssen Sie die Menge der verkauften Tickets mit 5 multiplizieren, um den Geldbetrag zu finden. Daher kann die Funktion als geschrieben werden M (t) = 5t. - Zum Beispiel, wenn sie 2 Tickets verkauft, müssen Sie 2 mal 5 multiplizieren, um 10 zu bekommen, die Menge an Dollar, die sie bekommen wird.
-
 3 Ermitteln Sie die Domäne. Um den Bereich zu bestimmen, müssen Sie zuerst die Domäne finden. Die Domäne enthält alle möglichen Werte von t, die in der Gleichung funktionieren. In diesem Fall kann Becky 0 oder mehr Tickets verkaufen - sie kann keine negativen Tickets verkaufen. Da wir die Anzahl der Plätze in ihrem Schulsaal nicht kennen, können wir annehmen, dass sie theoretisch unendlich viele Karten verkaufen kann. Und sie kann nur ganze Tickets verkaufen; sie kann zum Beispiel 1/2 eines Tickets nicht verkaufen. Daher ist die Domäne der Funktion t = jede nicht negative ganze Zahl.
3 Ermitteln Sie die Domäne. Um den Bereich zu bestimmen, müssen Sie zuerst die Domäne finden. Die Domäne enthält alle möglichen Werte von t, die in der Gleichung funktionieren. In diesem Fall kann Becky 0 oder mehr Tickets verkaufen - sie kann keine negativen Tickets verkaufen. Da wir die Anzahl der Plätze in ihrem Schulsaal nicht kennen, können wir annehmen, dass sie theoretisch unendlich viele Karten verkaufen kann. Und sie kann nur ganze Tickets verkaufen; sie kann zum Beispiel 1/2 eines Tickets nicht verkaufen. Daher ist die Domäne der Funktion t = jede nicht negative ganze Zahl. -
 4 Bestimmen Sie den Bereich. Die Bandbreite ist die mögliche Menge an Geld, die Becky aus ihrem Verkauf machen kann. Sie müssen mit der Domäne arbeiten, um den Bereich zu finden. Wenn Sie wissen, dass die Domäne eine beliebige nicht negative Ganzzahl ist und dass die Formel lautet M (t) = 5tDann wissen Sie, dass Sie alle nicht negativen Ganzzahlen in diese Funktion einfügen können, um die Ausgabe oder den Bereich zu erhalten. Zum Beispiel, wenn sie 5 Tickets verkauft, dann M (5) = 5 x 5 oder 25 Dollar. Wenn sie 100 verkauft, dann M (100) = 5 x 100 oder 500 Dollar. Daher ist der Bereich der Funktion jede nicht negative ganze Zahl, die ein Vielfaches von fünf ist.
4 Bestimmen Sie den Bereich. Die Bandbreite ist die mögliche Menge an Geld, die Becky aus ihrem Verkauf machen kann. Sie müssen mit der Domäne arbeiten, um den Bereich zu finden. Wenn Sie wissen, dass die Domäne eine beliebige nicht negative Ganzzahl ist und dass die Formel lautet M (t) = 5tDann wissen Sie, dass Sie alle nicht negativen Ganzzahlen in diese Funktion einfügen können, um die Ausgabe oder den Bereich zu erhalten. Zum Beispiel, wenn sie 5 Tickets verkauft, dann M (5) = 5 x 5 oder 25 Dollar. Wenn sie 100 verkauft, dann M (100) = 5 x 100 oder 500 Dollar. Daher ist der Bereich der Funktion jede nicht negative ganze Zahl, die ein Vielfaches von fünf ist. - Das bedeutet, dass jede nicht negative ganze Zahl, die ein Vielfaches von fünf ist, eine mögliche Ausgabe für die Eingabe der Funktion ist.
 Minotauromaquia
Minotauromaquia
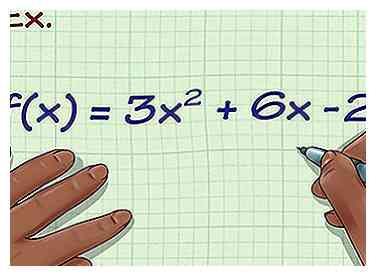 1 Schreiben Sie die Formel auf. Nehmen wir an, die Formel, mit der Sie arbeiten, lautet wie folgt: f (x) = 3x2 + 6x -2. Dies bedeutet, dass wenn Sie einen platzieren x in die Gleichung bekommen Sie Ihre y Wert. Dies ist die Funktion einer Parabel.
1 Schreiben Sie die Formel auf. Nehmen wir an, die Formel, mit der Sie arbeiten, lautet wie folgt: f (x) = 3x2 + 6x -2. Dies bedeutet, dass wenn Sie einen platzieren x in die Gleichung bekommen Sie Ihre y Wert. Dies ist die Funktion einer Parabel. 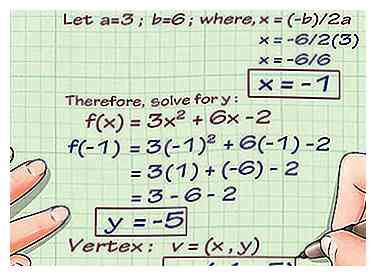 2 Suchen Sie den Eckpunkt der Funktion, wenn sie quadratisch ist. Wenn Sie mit einer geraden Linie oder einer Funktion mit einem Polynom einer ungeraden Zahl arbeiten, z. B. f (x) = 6x3+ 2x + 7, können Sie diesen Schritt überspringen. Aber wenn Sie mit einer Parabel oder einer Gleichung arbeiten, bei der die x-Koordinate quadriert oder auf eine gerade Potenz erhöht wird, müssen Sie den Scheitelpunkt plotten. Verwenden Sie dazu einfach die Formel -b / 2a um die x-Koordinate der Funktion 3x zu erhalten2 + 6x -2, wobei 3 = a, 6 = b und -2 = c. In diesem Fall -b ist -6 und 2a ist 6, also ist die x-Koordinate -6/6 oder -1.
2 Suchen Sie den Eckpunkt der Funktion, wenn sie quadratisch ist. Wenn Sie mit einer geraden Linie oder einer Funktion mit einem Polynom einer ungeraden Zahl arbeiten, z. B. f (x) = 6x3+ 2x + 7, können Sie diesen Schritt überspringen. Aber wenn Sie mit einer Parabel oder einer Gleichung arbeiten, bei der die x-Koordinate quadriert oder auf eine gerade Potenz erhöht wird, müssen Sie den Scheitelpunkt plotten. Verwenden Sie dazu einfach die Formel -b / 2a um die x-Koordinate der Funktion 3x zu erhalten2 + 6x -2, wobei 3 = a, 6 = b und -2 = c. In diesem Fall -b ist -6 und 2a ist 6, also ist die x-Koordinate -6/6 oder -1.  3 Finde ein paar andere Punkte in der Funktion. Um ein Gefühl für die Funktion zu bekommen, sollten Sie ein paar andere x-Koordinaten einstecken, damit Sie einen Eindruck davon bekommen, wie die Funktion aussieht, bevor Sie nach dem Bereich suchen. Da ist es eine Parabel und das x2 Koordinate ist positiv, es wird nach oben zeigen. Aber um Ihre Basen zu bedecken, lassen Sie uns einige x-Koordinaten einstecken, um zu sehen, welche y-Koordinaten sie liefern:
3 Finde ein paar andere Punkte in der Funktion. Um ein Gefühl für die Funktion zu bekommen, sollten Sie ein paar andere x-Koordinaten einstecken, damit Sie einen Eindruck davon bekommen, wie die Funktion aussieht, bevor Sie nach dem Bereich suchen. Da ist es eine Parabel und das x2 Koordinate ist positiv, es wird nach oben zeigen. Aber um Ihre Basen zu bedecken, lassen Sie uns einige x-Koordinaten einstecken, um zu sehen, welche y-Koordinaten sie liefern:  4 Finde den Bereich in der Grafik. Betrachten Sie nun die y-Koordinaten in der Grafik und finden Sie den tiefsten Punkt, an dem der Graph eine y-Koordinate berührt. In diesem Fall befindet sich die niedrigste y-Koordinate am Scheitelpunkt -5, und der Graph erstreckt sich unendlich über diesen Punkt. Dies bedeutet, dass der Bereich der Funktion ist y = alle reellen Zahlen ≥ -5.
4 Finde den Bereich in der Grafik. Betrachten Sie nun die y-Koordinaten in der Grafik und finden Sie den tiefsten Punkt, an dem der Graph eine y-Koordinate berührt. In diesem Fall befindet sich die niedrigste y-Koordinate am Scheitelpunkt -5, und der Graph erstreckt sich unendlich über diesen Punkt. Dies bedeutet, dass der Bereich der Funktion ist y = alle reellen Zahlen ≥ -5.  1 Finde das Minimum der Funktion. Suchen Sie nach der niedrigsten Y-Koordinate der Funktion. Nehmen wir an, die Funktion erreicht ihren niedrigsten Punkt bei -3. Diese Funktion könnte auch unendlich kleiner werden, so dass sie keinen tiefsten Punkt hat - nur unendlich.
1 Finde das Minimum der Funktion. Suchen Sie nach der niedrigsten Y-Koordinate der Funktion. Nehmen wir an, die Funktion erreicht ihren niedrigsten Punkt bei -3. Diese Funktion könnte auch unendlich kleiner werden, so dass sie keinen tiefsten Punkt hat - nur unendlich.  2 Finde das Maximum der Funktion. Nehmen wir an, die höchste y-Koordinate, die die Funktion erreicht, ist 10. Diese Funktion könnte auch unendlich größer werden, also hat sie keinen höchsten Punkt - nur unendlich.
2 Finde das Maximum der Funktion. Nehmen wir an, die höchste y-Koordinate, die die Funktion erreicht, ist 10. Diese Funktion könnte auch unendlich größer werden, also hat sie keinen höchsten Punkt - nur unendlich.  3 Geben Sie den Bereich an. Dies bedeutet, dass der Bereich der Funktion oder der Bereich der y-Koordinaten von -3 bis 10 reicht. Also, -3 ≤ f (x) ≤ 10. Das ist der Bereich der Funktion.
3 Geben Sie den Bereich an. Dies bedeutet, dass der Bereich der Funktion oder der Bereich der y-Koordinaten von -3 bis 10 reicht. Also, -3 ≤ f (x) ≤ 10. Das ist der Bereich der Funktion.  1 Schreiben Sie die Beziehung auf. Eine Relation ist eine Menge geordneter Paare mit x- und y-Koordinaten. Sie können eine Beziehung betrachten und ihre Domäne und ihren Bereich bestimmen. Nehmen wir an, Sie arbeiten mit der folgenden Beziehung: (2, -3), (4, 6), (3, -1), (6, 6), (2, 3).[1]
1 Schreiben Sie die Beziehung auf. Eine Relation ist eine Menge geordneter Paare mit x- und y-Koordinaten. Sie können eine Beziehung betrachten und ihre Domäne und ihren Bereich bestimmen. Nehmen wir an, Sie arbeiten mit der folgenden Beziehung: (2, -3), (4, 6), (3, -1), (6, 6), (2, 3).[1]  2 Listen Sie die y-Koordinaten der Relation auf. Um den Bereich der Beziehung zu finden, schreiben Sie einfach alle y-Koordinaten jedes geordneten Paares auf: -3, 6, -1, 6, 3.[2]
2 Listen Sie die y-Koordinaten der Relation auf. Um den Bereich der Beziehung zu finden, schreiben Sie einfach alle y-Koordinaten jedes geordneten Paares auf: -3, 6, -1, 6, 3.[2]  3 Entfernen Sie alle doppelten Koordinaten, so dass Sie nur eine von jeder Y-Koordinate haben. Sie werden feststellen, dass Sie zweimal "6" aufgelistet haben. Nimm es raus, so dass du -3, -1, 6, 3 übrig hast.[3]
3 Entfernen Sie alle doppelten Koordinaten, so dass Sie nur eine von jeder Y-Koordinate haben. Sie werden feststellen, dass Sie zweimal "6" aufgelistet haben. Nimm es raus, so dass du -3, -1, 6, 3 übrig hast.[3] 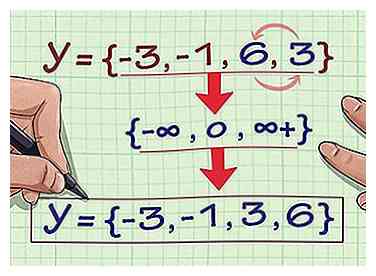 4 Schreiben Sie den Bereich der Beziehung in aufsteigender Reihenfolge. Ordnen Sie nun die Zahlen im Satz neu an, so dass Sie vom kleinsten zum größten übergehen und Ihre Reichweite haben. Der Bereich der Beziehung (2, -3), (4, 6), (3, -1), (6, 6), (2, 3) ist -3, -1, 3, 6 . Du bist fertig.[4]
4 Schreiben Sie den Bereich der Beziehung in aufsteigender Reihenfolge. Ordnen Sie nun die Zahlen im Satz neu an, so dass Sie vom kleinsten zum größten übergehen und Ihre Reichweite haben. Der Bereich der Beziehung (2, -3), (4, 6), (3, -1), (6, 6), (2, 3) ist -3, -1, 3, 6 . Du bist fertig.[4]  5 Stellen Sie sicher, dass die Beziehung ist eine Funktion. Damit eine Relation eine Funktion ist, muss die y-Koordinate bei jeder Eingabe einer x-Koordinate gleich sein. Zum Beispiel ist die Beziehung (2, 3) (2, 4) (6, 9) nicht eine Funktion, denn wenn du zum ersten Mal 2 als x eingibst, hast du eine 3, aber das zweite Mal, wenn du eine 2 eingibst, hast du eine Vier. Damit eine Beziehung eine Funktion ist, sollten Sie, wenn Sie dieselbe Eingabe eingeben, immer dieselbe Ausgabe erhalten. Wenn Sie eine -7 eingeben, sollten Sie jedes Mal die gleiche y-Koordinate erhalten (was auch immer es sein mag).[5]
5 Stellen Sie sicher, dass die Beziehung ist eine Funktion. Damit eine Relation eine Funktion ist, muss die y-Koordinate bei jeder Eingabe einer x-Koordinate gleich sein. Zum Beispiel ist die Beziehung (2, 3) (2, 4) (6, 9) nicht eine Funktion, denn wenn du zum ersten Mal 2 als x eingibst, hast du eine 3, aber das zweite Mal, wenn du eine 2 eingibst, hast du eine Vier. Damit eine Beziehung eine Funktion ist, sollten Sie, wenn Sie dieselbe Eingabe eingeben, immer dieselbe Ausgabe erhalten. Wenn Sie eine -7 eingeben, sollten Sie jedes Mal die gleiche y-Koordinate erhalten (was auch immer es sein mag).[5]  1 Lesen Sie das Problem. Nehmen wir an, Sie arbeiten mit folgendem Problem: "Becky verkauft Tickets für die Talentshow ihrer Schule für jeweils 5 Dollar. Die Menge an Geld, die sie sammelt, hängt davon ab, wie viele Tickets sie verkauft. Was ist der Umfang der Funktion?"
1 Lesen Sie das Problem. Nehmen wir an, Sie arbeiten mit folgendem Problem: "Becky verkauft Tickets für die Talentshow ihrer Schule für jeweils 5 Dollar. Die Menge an Geld, die sie sammelt, hängt davon ab, wie viele Tickets sie verkauft. Was ist der Umfang der Funktion?"  2 Schreiben Sie das Problem als eine Funktion. In diesem Fall, M stellt den Geldbetrag dar, den sie sammelt, und t stellt die Menge an Tickets dar, die sie verkauft.Da jedoch jedes Ticket 5 Dollar kostet, müssen Sie die Menge der verkauften Tickets mit 5 multiplizieren, um den Geldbetrag zu finden. Daher kann die Funktion als geschrieben werden M (t) = 5t.
2 Schreiben Sie das Problem als eine Funktion. In diesem Fall, M stellt den Geldbetrag dar, den sie sammelt, und t stellt die Menge an Tickets dar, die sie verkauft.Da jedoch jedes Ticket 5 Dollar kostet, müssen Sie die Menge der verkauften Tickets mit 5 multiplizieren, um den Geldbetrag zu finden. Daher kann die Funktion als geschrieben werden M (t) = 5t.  3 Ermitteln Sie die Domäne. Um den Bereich zu bestimmen, müssen Sie zuerst die Domäne finden. Die Domäne enthält alle möglichen Werte von t, die in der Gleichung funktionieren. In diesem Fall kann Becky 0 oder mehr Tickets verkaufen - sie kann keine negativen Tickets verkaufen. Da wir die Anzahl der Plätze in ihrem Schulsaal nicht kennen, können wir annehmen, dass sie theoretisch unendlich viele Karten verkaufen kann. Und sie kann nur ganze Tickets verkaufen; sie kann zum Beispiel 1/2 eines Tickets nicht verkaufen. Daher ist die Domäne der Funktion t = jede nicht negative ganze Zahl.
3 Ermitteln Sie die Domäne. Um den Bereich zu bestimmen, müssen Sie zuerst die Domäne finden. Die Domäne enthält alle möglichen Werte von t, die in der Gleichung funktionieren. In diesem Fall kann Becky 0 oder mehr Tickets verkaufen - sie kann keine negativen Tickets verkaufen. Da wir die Anzahl der Plätze in ihrem Schulsaal nicht kennen, können wir annehmen, dass sie theoretisch unendlich viele Karten verkaufen kann. Und sie kann nur ganze Tickets verkaufen; sie kann zum Beispiel 1/2 eines Tickets nicht verkaufen. Daher ist die Domäne der Funktion t = jede nicht negative ganze Zahl.  4 Bestimmen Sie den Bereich. Die Bandbreite ist die mögliche Menge an Geld, die Becky aus ihrem Verkauf machen kann. Sie müssen mit der Domäne arbeiten, um den Bereich zu finden. Wenn Sie wissen, dass die Domäne eine beliebige nicht negative Ganzzahl ist und dass die Formel lautet M (t) = 5tDann wissen Sie, dass Sie alle nicht negativen Ganzzahlen in diese Funktion einfügen können, um die Ausgabe oder den Bereich zu erhalten. Zum Beispiel, wenn sie 5 Tickets verkauft, dann M (5) = 5 x 5 oder 25 Dollar. Wenn sie 100 verkauft, dann M (100) = 5 x 100 oder 500 Dollar. Daher ist der Bereich der Funktion jede nicht negative ganze Zahl, die ein Vielfaches von fünf ist.
4 Bestimmen Sie den Bereich. Die Bandbreite ist die mögliche Menge an Geld, die Becky aus ihrem Verkauf machen kann. Sie müssen mit der Domäne arbeiten, um den Bereich zu finden. Wenn Sie wissen, dass die Domäne eine beliebige nicht negative Ganzzahl ist und dass die Formel lautet M (t) = 5tDann wissen Sie, dass Sie alle nicht negativen Ganzzahlen in diese Funktion einfügen können, um die Ausgabe oder den Bereich zu erhalten. Zum Beispiel, wenn sie 5 Tickets verkauft, dann M (5) = 5 x 5 oder 25 Dollar. Wenn sie 100 verkauft, dann M (100) = 5 x 100 oder 500 Dollar. Daher ist der Bereich der Funktion jede nicht negative ganze Zahl, die ein Vielfaches von fünf ist.