Die Domäne einer Funktion ist die Menge von Zahlen, die zu einer bestimmten Funktion gehören können. Mit anderen Worten, es ist die Menge von x-Werten, die Sie in eine gegebene Gleichung einfügen können. Die Menge möglicher y-Werte wird als Bereich bezeichnet. Wenn Sie wissen möchten, wie Sie die Domäne einer Funktion in verschiedenen Situationen finden, folgen Sie einfach diesen Schritten.
Methode eins von sechs:
Die Grundlagen lernen
-
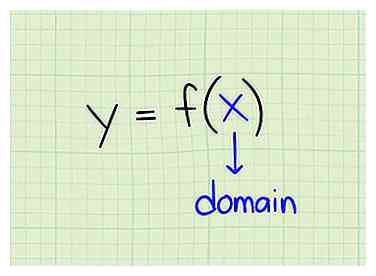 1 Lerne die Definition der Domain. Die Domäne ist definiert als die Menge von Eingabewerten, für die die Funktion einen Ausgabewert erzeugt. Mit anderen Worten, die Domäne ist die vollständige Menge von x-Werten, die in eine Funktion eingefügt werden können, um einen y-Wert zu erzeugen.
1 Lerne die Definition der Domain. Die Domäne ist definiert als die Menge von Eingabewerten, für die die Funktion einen Ausgabewert erzeugt. Mit anderen Worten, die Domäne ist die vollständige Menge von x-Werten, die in eine Funktion eingefügt werden können, um einen y-Wert zu erzeugen. -
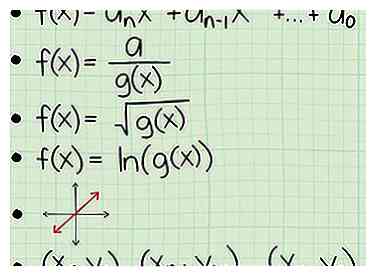 2 Erfahren Sie, wie Sie die Domäne einer Vielzahl von Funktionen finden. Die Art der Funktion bestimmt die beste Methode, um eine Domain zu finden. Hier sind die Grundlagen, die Sie über jede Art von Funktion wissen müssen, die im nächsten Abschnitt erklärt wird:
2 Erfahren Sie, wie Sie die Domäne einer Vielzahl von Funktionen finden. Die Art der Funktion bestimmt die beste Methode, um eine Domain zu finden. Hier sind die Grundlagen, die Sie über jede Art von Funktion wissen müssen, die im nächsten Abschnitt erklärt wird: - Eine Polynomfunktion ohne Radikale oder Variablen im Nenner. Für diese Art von Funktion sind die Domänen alle reellen Zahlen.
- Eine Funktion mit einem Bruchteil einer Variablen im Nenner. Um die Domäne dieses Funktionstyps zu finden, setzen Sie den unteren Wert auf Null und schließen Sie den x-Wert aus, den Sie beim Lösen der Gleichung finden.
- Eine Funktion mit einer Variablen innerhalb eines radikalen Zeichens. Um die Domäne dieses Funktionstyps zu finden, setzen Sie einfach die Terme innerhalb des Radikalzeichens auf> 0 und lösen Sie, um die Werte zu finden, die für x funktionieren würden.
- Eine Funktion, die den natürlichen Log (ln) verwendet. Stellen Sie einfach die Begriffe in Klammern auf> 0 und lösen Sie.
- Ein Graph. Sehen Sie sich das Diagramm an, um zu sehen, welche Werte für x gelten.
- Eine Relation. Dies wird eine Liste von X- und Y-Koordinaten sein. Ihre Domain wird einfach eine Liste von x Koordinaten sein.
-
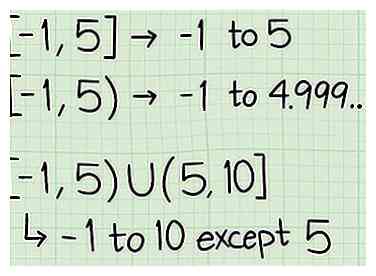 3 Geben Sie die Domäne richtig an. Die richtige Schreibweise für die Domäne ist leicht zu erlernen, aber es ist wichtig, dass Sie sie richtig schreiben, um die richtige Antwort auszudrücken und volle Punkte für Aufgaben und Tests zu erhalten. Hier sind ein paar Dinge, die Sie über das Schreiben der Domäne einer Funktion wissen müssen:
3 Geben Sie die Domäne richtig an. Die richtige Schreibweise für die Domäne ist leicht zu erlernen, aber es ist wichtig, dass Sie sie richtig schreiben, um die richtige Antwort auszudrücken und volle Punkte für Aufgaben und Tests zu erhalten. Hier sind ein paar Dinge, die Sie über das Schreiben der Domäne einer Funktion wissen müssen: - Das Format zum Ausdrücken der Domäne ist eine offene Klammer / Klammer, gefolgt von den 2 Endpunkten der Domäne, getrennt durch ein Komma, gefolgt von einer geschlossenen Klammer / Klammer.
- Zum Beispiel, [-1,5]. Dies bedeutet, dass die Domäne von -1 bis 5 reicht.
- Verwenden Sie Klammern wie z [ und ] um anzuzeigen, dass eine Nummer in der Domäne enthalten ist.
- In dem Beispiel [-1,5] enthält die Domäne -1.
- Verwenden Sie Klammern wie z ( und ) um anzuzeigen, dass eine Nummer nicht in der Domain enthalten ist.
- Also im Beispiel, [-1,5), ist 5 nicht in der Domäne enthalten. Die Domäne endet willkürlich kurz vor 5, d. H. 4.999 ...
- Verwenden Sie "U" ("Union"), um Teile der Domäne zu verbinden, die durch eine Lücke getrennt sind.
- Zum Beispiel, [-1,5) U (5,10]. Dies bedeutet, dass die Domäne von -1 bis einschließlich 10 reicht, aber dass es in der Domäne bei 5 eine Lücke gibt. Dies könnte das Ergebnis von sein, z Beispiel eine Funktion mit "x - 5" im Nenner.
- Sie können beliebig viele "U" -Symbole verwenden, wenn die Domäne mehrere Lücken enthält.
- Verwenden Sie Unendlichkeits- und negative Unendlichkeitszeichen, um auszudrücken, dass der Bereich unendlich in beiden Richtungen verläuft.
- Verwenden Sie immer (), nicht [], mit Unendlichkeitssymbolen.
- Das Format zum Ausdrücken der Domäne ist eine offene Klammer / Klammer, gefolgt von den 2 Endpunkten der Domäne, getrennt durch ein Komma, gefolgt von einer geschlossenen Klammer / Klammer.
Methode zwei von sechs:
Finden der Domäne einer Funktion mit einer Fraktion
-
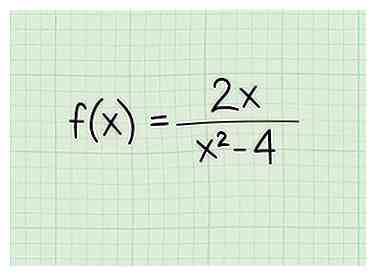 1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit folgendem Problem:
1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit folgendem Problem: - f (x) = 2x / (x2 - 4)
-
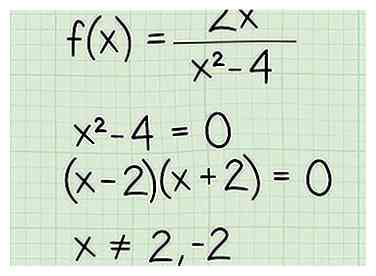 2 Setzen Sie den Nenner für Brüche mit einer Variablen im Nenner auf Null. Wenn Sie die Domäne einer Bruchfunktion finden, müssen Sie alle x-Werte ausschließen, die den Nenner gleich Null machen, da Sie niemals durch Null dividieren können. Schreiben Sie den Nenner als eine Gleichung und setzen Sie ihn gleich 0. So machen Sie das:
2 Setzen Sie den Nenner für Brüche mit einer Variablen im Nenner auf Null. Wenn Sie die Domäne einer Bruchfunktion finden, müssen Sie alle x-Werte ausschließen, die den Nenner gleich Null machen, da Sie niemals durch Null dividieren können. Schreiben Sie den Nenner als eine Gleichung und setzen Sie ihn gleich 0. So machen Sie das: - f (x) = 2x / (x2 - 4)
- x2 - 4 = 0
- (x - 2) (x + 2) = 0
- x ≠ (2, - 2)
-
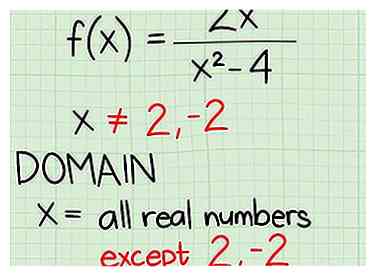 3 Geben Sie die Domäne an. Hier ist, wie Sie es tun:
3 Geben Sie die Domäne an. Hier ist, wie Sie es tun: - x = alle reellen Zahlen außer 2 und -2
Methode drei von sechs:
Finden der Domäne einer Funktion mit einer Quadratwurzel
-
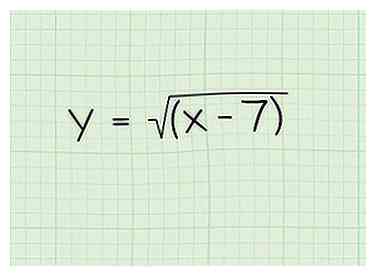 1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit folgendem Problem: Y = √ (x-7)
1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit folgendem Problem: Y = √ (x-7) -
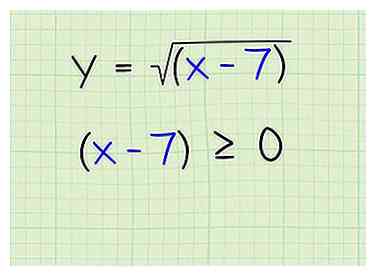 2 Setzen Sie die Begriffe innerhalb des Radikanden auf größer oder gleich 0. Sie können die Quadratwurzel einer negativen Zahl nicht verwenden, obwohl Sie die Quadratwurzel von 0 verwenden können. Stellen Sie also die Terme innerhalb des Radikanden auf größer als oder gleich 0. Beachten Sie, dass dies nicht nur für Quadratwurzeln gilt, sondern auch für alle geraden Wurzeln. Es gilt jedoch nicht für ungeradzahlige Wurzeln, da es völlig in Ordnung ist, unter ungeraden Wurzeln Negative zu haben. Hier ist wie:
2 Setzen Sie die Begriffe innerhalb des Radikanden auf größer oder gleich 0. Sie können die Quadratwurzel einer negativen Zahl nicht verwenden, obwohl Sie die Quadratwurzel von 0 verwenden können. Stellen Sie also die Terme innerhalb des Radikanden auf größer als oder gleich 0. Beachten Sie, dass dies nicht nur für Quadratwurzeln gilt, sondern auch für alle geraden Wurzeln. Es gilt jedoch nicht für ungeradzahlige Wurzeln, da es völlig in Ordnung ist, unter ungeraden Wurzeln Negative zu haben. Hier ist wie: - x-7 ≧ 0
-
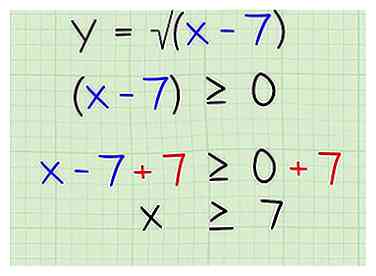 3 Isoliere die Variable. Nun, um x auf der linken Seite der Gleichung zu isolieren, füge einfach 7 zu beiden Seiten hinzu, so dass du das Folgende übrig hast:
3 Isoliere die Variable. Nun, um x auf der linken Seite der Gleichung zu isolieren, füge einfach 7 zu beiden Seiten hinzu, so dass du das Folgende übrig hast: - x ≧ 7
-
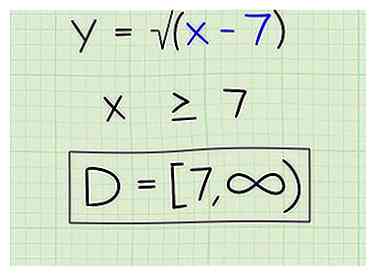 4 Geben Sie die Domäne korrekt an. Hier ist, wie Sie es schreiben würden:
4 Geben Sie die Domäne korrekt an. Hier ist, wie Sie es schreiben würden: - D = [7, ∞)
-
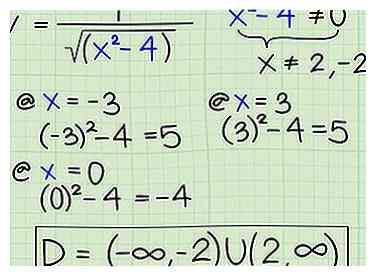 5 Suchen Sie die Domäne einer Funktion mit einer Quadratwurzel, wenn mehrere Lösungen vorhanden sind. Nehmen wir an, Sie arbeiten mit der folgenden Funktion: Y = 1 / √ (̅x2 -4). Wenn Sie den Nenner faktorisieren und ihn auf Null setzen, erhalten Sie x ≠ (2, - 2). Hier geht's von dort:
5 Suchen Sie die Domäne einer Funktion mit einer Quadratwurzel, wenn mehrere Lösungen vorhanden sind. Nehmen wir an, Sie arbeiten mit der folgenden Funktion: Y = 1 / √ (̅x2 -4). Wenn Sie den Nenner faktorisieren und ihn auf Null setzen, erhalten Sie x ≠ (2, - 2). Hier geht's von dort: - Überprüfen Sie nun den Bereich unter -2 (z. B. durch Einstecken von -3), um zu sehen, ob die Zahlen unter -2 in den Nenner eingesteckt werden können, um eine Zahl größer als 0 zu erhalten.
- (-3)2 - 4 = 5
- Überprüfen Sie nun den Bereich zwischen -2 und 2. Wählen Sie zum Beispiel 0 aus.
- 02 - 4 = -4, also wissen Sie, dass die Zahlen zwischen -2 und 2 nicht funktionieren.
- Versuchen Sie jetzt eine Zahl über 2, z. B. +3.
- 32 - 4 = 5, also funktionieren die Zahlen über 2.
- Schreiben Sie die Domäne, wenn Sie fertig sind. So würden Sie die Domain schreiben:
- D = (-∞, -2) U (2, ∞)
- Überprüfen Sie nun den Bereich unter -2 (z. B. durch Einstecken von -3), um zu sehen, ob die Zahlen unter -2 in den Nenner eingesteckt werden können, um eine Zahl größer als 0 zu erhalten.
Methode vier von sechs:
Finden der Domain einer Funktion mit einem Natural Log
-
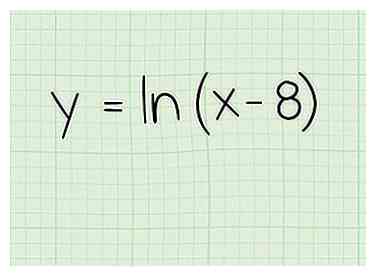 1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit diesem:
1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit diesem: - f (x) = ln (x-8)
-
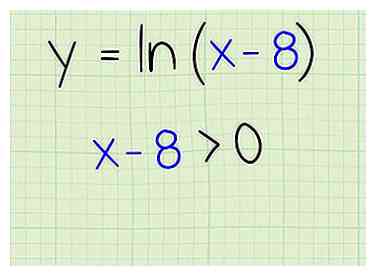 2 Legen Sie die Begriffe innerhalb der Klammern auf größer als null fest. Der natürliche Log muss eine positive Zahl sein, also setze die Begriffe innerhalb der Klammern auf größer als Null, um es zu machen. Hier ist was du tust:
2 Legen Sie die Begriffe innerhalb der Klammern auf größer als null fest. Der natürliche Log muss eine positive Zahl sein, also setze die Begriffe innerhalb der Klammern auf größer als Null, um es zu machen. Hier ist was du tust: - x - 8> 0
-
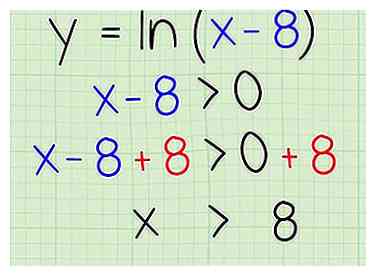 3 Lösen. Isolieren Sie einfach die Variable x, indem Sie beiden Seiten 8 hinzufügen. Hier ist wie:
3 Lösen. Isolieren Sie einfach die Variable x, indem Sie beiden Seiten 8 hinzufügen. Hier ist wie: - x - 8 + 8> 0 + 8
- x> 8
-
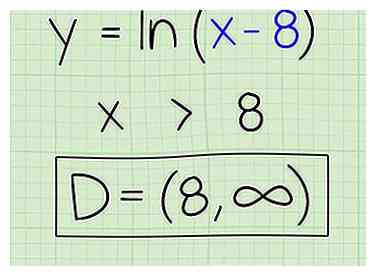 4 Geben Sie die Domäne an. Zeigen Sie, dass die Domäne für diese Gleichung allen Zahlen größer als 8 bis unendlich entspricht. Hier ist wie:
4 Geben Sie die Domäne an. Zeigen Sie, dass die Domäne für diese Gleichung allen Zahlen größer als 8 bis unendlich entspricht. Hier ist wie: - D = (8, ∞)
Methode fünf von sechs:
Suchen der Domäne einer Funktion mithilfe eines Diagramms
-
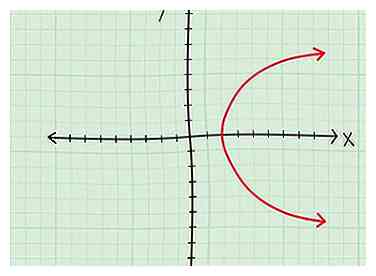 1 Schau dir das Diagramm an.
1 Schau dir das Diagramm an. -
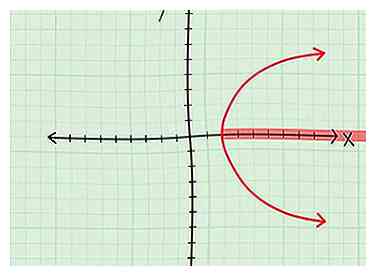 2 Überprüfen Sie die x-Werte, die in der Grafik enthalten sind. Das ist vielleicht einfacher gesagt als getan, aber hier sind einige Tipps:
2 Überprüfen Sie die x-Werte, die in der Grafik enthalten sind. Das ist vielleicht einfacher gesagt als getan, aber hier sind einige Tipps: - Eine Linie. Wenn Sie im Diagramm eine Linie sehen, die sich bis unendlich erstreckt, dann alle Versionen von x werden schließlich abgedeckt, so dass die Domain allen reellen Zahlen entspricht.
- Eine normale Parabel. Wenn Sie eine Parabel sehen, die nach oben oder unten zeigt, dann ist die Domäne alle reellen Zahlen, weil alle Zahlen auf der x-Achse schließlich bedeckt sein werden.
- Eine Seitparabel. Nun, wenn Sie eine Parabel mit einem Eckpunkt bei (4,0) haben, der sich unendlich nach rechts erstreckt, dann ist Ihre Domäne D = [4, ∞)
-
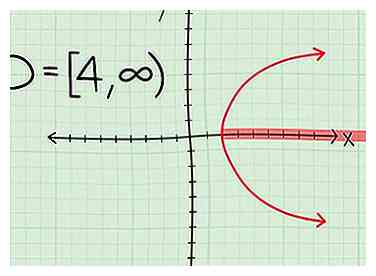 3 Geben Sie die Domäne an. Geben Sie die Domäne einfach basierend auf dem Grafiktyp an, mit dem Sie arbeiten. Wenn Sie unsicher sind und die Gleichung der Linie kennen, stecken Sie die X-Koordinaten wieder in die zu überprüfende Funktion.
3 Geben Sie die Domäne an. Geben Sie die Domäne einfach basierend auf dem Grafiktyp an, mit dem Sie arbeiten. Wenn Sie unsicher sind und die Gleichung der Linie kennen, stecken Sie die X-Koordinaten wieder in die zu überprüfende Funktion.
Methode sechs von sechs:
Finden der Domäne einer Funktion unter Verwendung einer Beziehung
-
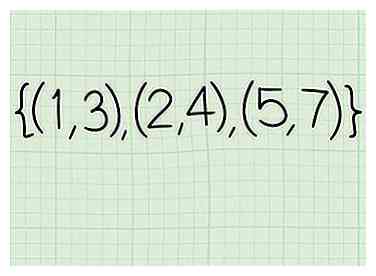 1 Schreiben Sie die Beziehung auf. Eine Beziehung ist nur eine Menge von x- und y-Koordinaten. Nehmen wir an, Sie arbeiten mit den folgenden Koordinaten: (1, 3), (2, 4), (5, 7)
1 Schreiben Sie die Beziehung auf. Eine Beziehung ist nur eine Menge von x- und y-Koordinaten. Nehmen wir an, Sie arbeiten mit den folgenden Koordinaten: (1, 3), (2, 4), (5, 7) -
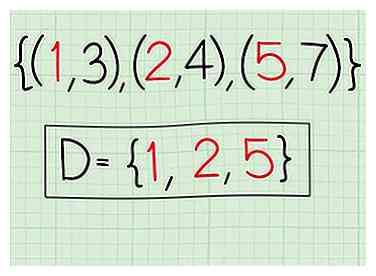 2 Schreiben Sie die x-Koordinaten auf. Sie sind: 1, 2, 5.
2 Schreiben Sie die x-Koordinaten auf. Sie sind: 1, 2, 5. -
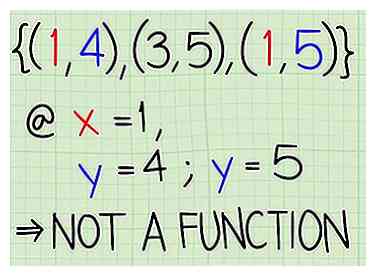 3 Geben Sie die Domäne an. D = 1, 2, 5
3 Geben Sie die Domäne an. D = 1, 2, 5 - 4 Stellen Sie sicher, dass die Beziehung eine Funktion ist. Damit eine Beziehung eine Funktion ist, sollten Sie bei jeder Eingabe einer numerischen x-Koordinate die gleiche y-Koordinate erhalten. Also, wenn Sie 3 für x eingeben, sollten Sie immer 6 für y bekommen, und so weiter. Die folgende Beziehung ist nicht eine Funktion, weil Sie für jeden Wert von "x" zwei verschiedene Werte von "y" erhalten: (1, 4), (3, 5), (1, 5).[1]
 Minotauromaquia
Minotauromaquia
 1 Lerne die Definition der Domain. Die Domäne ist definiert als die Menge von Eingabewerten, für die die Funktion einen Ausgabewert erzeugt. Mit anderen Worten, die Domäne ist die vollständige Menge von x-Werten, die in eine Funktion eingefügt werden können, um einen y-Wert zu erzeugen.
1 Lerne die Definition der Domain. Die Domäne ist definiert als die Menge von Eingabewerten, für die die Funktion einen Ausgabewert erzeugt. Mit anderen Worten, die Domäne ist die vollständige Menge von x-Werten, die in eine Funktion eingefügt werden können, um einen y-Wert zu erzeugen. 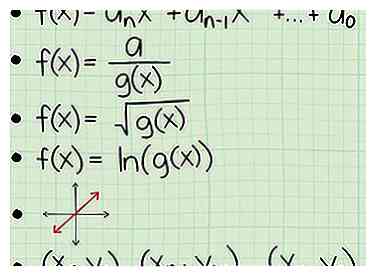 2 Erfahren Sie, wie Sie die Domäne einer Vielzahl von Funktionen finden. Die Art der Funktion bestimmt die beste Methode, um eine Domain zu finden. Hier sind die Grundlagen, die Sie über jede Art von Funktion wissen müssen, die im nächsten Abschnitt erklärt wird:
2 Erfahren Sie, wie Sie die Domäne einer Vielzahl von Funktionen finden. Die Art der Funktion bestimmt die beste Methode, um eine Domain zu finden. Hier sind die Grundlagen, die Sie über jede Art von Funktion wissen müssen, die im nächsten Abschnitt erklärt wird: 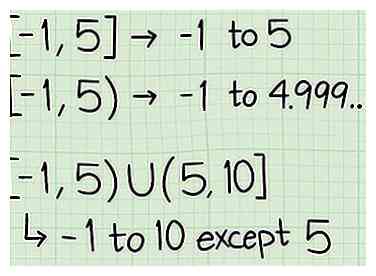 3 Geben Sie die Domäne richtig an. Die richtige Schreibweise für die Domäne ist leicht zu erlernen, aber es ist wichtig, dass Sie sie richtig schreiben, um die richtige Antwort auszudrücken und volle Punkte für Aufgaben und Tests zu erhalten. Hier sind ein paar Dinge, die Sie über das Schreiben der Domäne einer Funktion wissen müssen:
3 Geben Sie die Domäne richtig an. Die richtige Schreibweise für die Domäne ist leicht zu erlernen, aber es ist wichtig, dass Sie sie richtig schreiben, um die richtige Antwort auszudrücken und volle Punkte für Aufgaben und Tests zu erhalten. Hier sind ein paar Dinge, die Sie über das Schreiben der Domäne einer Funktion wissen müssen: 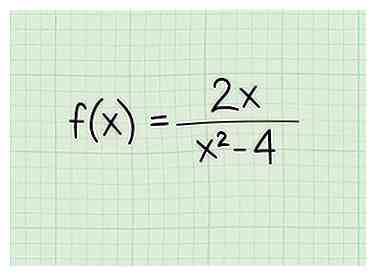 1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit folgendem Problem:
1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit folgendem Problem: 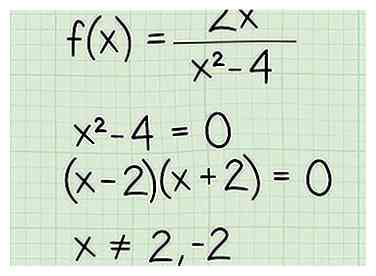 2 Setzen Sie den Nenner für Brüche mit einer Variablen im Nenner auf Null. Wenn Sie die Domäne einer Bruchfunktion finden, müssen Sie alle x-Werte ausschließen, die den Nenner gleich Null machen, da Sie niemals durch Null dividieren können. Schreiben Sie den Nenner als eine Gleichung und setzen Sie ihn gleich 0. So machen Sie das:
2 Setzen Sie den Nenner für Brüche mit einer Variablen im Nenner auf Null. Wenn Sie die Domäne einer Bruchfunktion finden, müssen Sie alle x-Werte ausschließen, die den Nenner gleich Null machen, da Sie niemals durch Null dividieren können. Schreiben Sie den Nenner als eine Gleichung und setzen Sie ihn gleich 0. So machen Sie das: 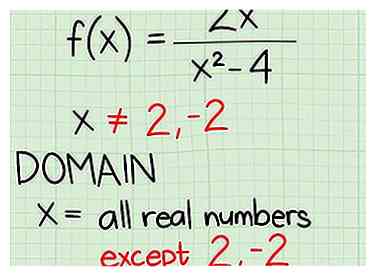 3 Geben Sie die Domäne an. Hier ist, wie Sie es tun:
3 Geben Sie die Domäne an. Hier ist, wie Sie es tun: 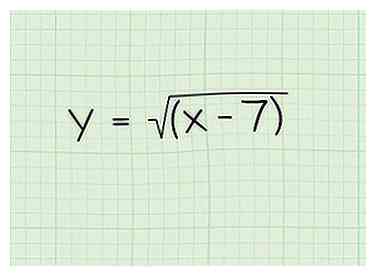 1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit folgendem Problem: Y = √ (x-7)
1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit folgendem Problem: Y = √ (x-7) 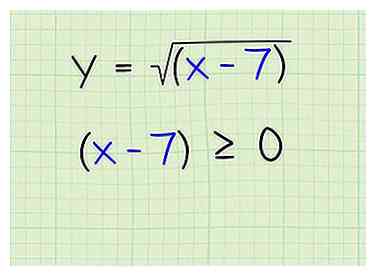 2 Setzen Sie die Begriffe innerhalb des Radikanden auf größer oder gleich 0. Sie können die Quadratwurzel einer negativen Zahl nicht verwenden, obwohl Sie die Quadratwurzel von 0 verwenden können. Stellen Sie also die Terme innerhalb des Radikanden auf größer als oder gleich 0. Beachten Sie, dass dies nicht nur für Quadratwurzeln gilt, sondern auch für alle geraden Wurzeln. Es gilt jedoch nicht für ungeradzahlige Wurzeln, da es völlig in Ordnung ist, unter ungeraden Wurzeln Negative zu haben. Hier ist wie:
2 Setzen Sie die Begriffe innerhalb des Radikanden auf größer oder gleich 0. Sie können die Quadratwurzel einer negativen Zahl nicht verwenden, obwohl Sie die Quadratwurzel von 0 verwenden können. Stellen Sie also die Terme innerhalb des Radikanden auf größer als oder gleich 0. Beachten Sie, dass dies nicht nur für Quadratwurzeln gilt, sondern auch für alle geraden Wurzeln. Es gilt jedoch nicht für ungeradzahlige Wurzeln, da es völlig in Ordnung ist, unter ungeraden Wurzeln Negative zu haben. Hier ist wie: 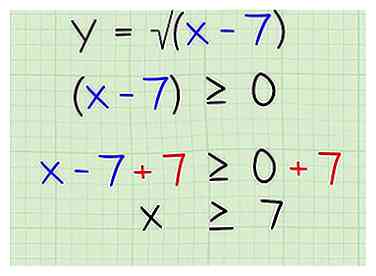 3 Isoliere die Variable. Nun, um x auf der linken Seite der Gleichung zu isolieren, füge einfach 7 zu beiden Seiten hinzu, so dass du das Folgende übrig hast:
3 Isoliere die Variable. Nun, um x auf der linken Seite der Gleichung zu isolieren, füge einfach 7 zu beiden Seiten hinzu, so dass du das Folgende übrig hast: 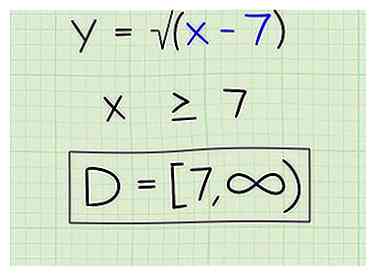 4 Geben Sie die Domäne korrekt an. Hier ist, wie Sie es schreiben würden:
4 Geben Sie die Domäne korrekt an. Hier ist, wie Sie es schreiben würden: 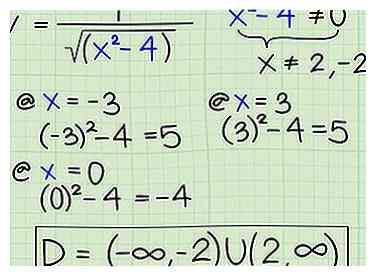 5 Suchen Sie die Domäne einer Funktion mit einer Quadratwurzel, wenn mehrere Lösungen vorhanden sind. Nehmen wir an, Sie arbeiten mit der folgenden Funktion: Y = 1 / √ (̅x2 -4). Wenn Sie den Nenner faktorisieren und ihn auf Null setzen, erhalten Sie x ≠ (2, - 2). Hier geht's von dort:
5 Suchen Sie die Domäne einer Funktion mit einer Quadratwurzel, wenn mehrere Lösungen vorhanden sind. Nehmen wir an, Sie arbeiten mit der folgenden Funktion: Y = 1 / √ (̅x2 -4). Wenn Sie den Nenner faktorisieren und ihn auf Null setzen, erhalten Sie x ≠ (2, - 2). Hier geht's von dort: 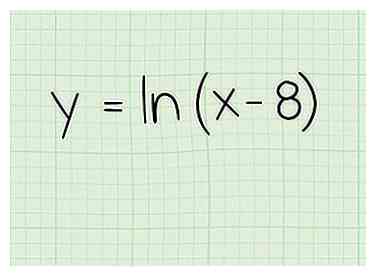 1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit diesem:
1 Schreibe das Problem auf. Nehmen wir an, Sie arbeiten mit diesem: 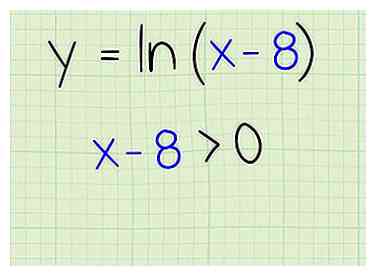 2 Legen Sie die Begriffe innerhalb der Klammern auf größer als null fest. Der natürliche Log muss eine positive Zahl sein, also setze die Begriffe innerhalb der Klammern auf größer als Null, um es zu machen. Hier ist was du tust:
2 Legen Sie die Begriffe innerhalb der Klammern auf größer als null fest. Der natürliche Log muss eine positive Zahl sein, also setze die Begriffe innerhalb der Klammern auf größer als Null, um es zu machen. Hier ist was du tust: 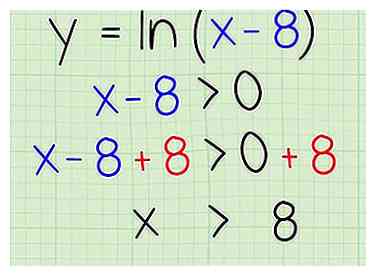 3 Lösen. Isolieren Sie einfach die Variable x, indem Sie beiden Seiten 8 hinzufügen. Hier ist wie:
3 Lösen. Isolieren Sie einfach die Variable x, indem Sie beiden Seiten 8 hinzufügen. Hier ist wie: 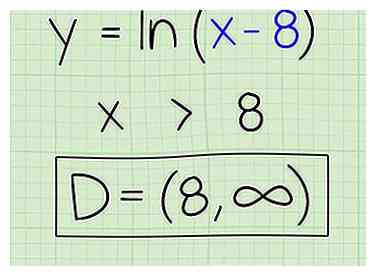 4 Geben Sie die Domäne an. Zeigen Sie, dass die Domäne für diese Gleichung allen Zahlen größer als 8 bis unendlich entspricht. Hier ist wie:
4 Geben Sie die Domäne an. Zeigen Sie, dass die Domäne für diese Gleichung allen Zahlen größer als 8 bis unendlich entspricht. Hier ist wie:  1 Schau dir das Diagramm an.
1 Schau dir das Diagramm an.  2 Überprüfen Sie die x-Werte, die in der Grafik enthalten sind. Das ist vielleicht einfacher gesagt als getan, aber hier sind einige Tipps:
2 Überprüfen Sie die x-Werte, die in der Grafik enthalten sind. Das ist vielleicht einfacher gesagt als getan, aber hier sind einige Tipps:  3 Geben Sie die Domäne an. Geben Sie die Domäne einfach basierend auf dem Grafiktyp an, mit dem Sie arbeiten. Wenn Sie unsicher sind und die Gleichung der Linie kennen, stecken Sie die X-Koordinaten wieder in die zu überprüfende Funktion.
3 Geben Sie die Domäne an. Geben Sie die Domäne einfach basierend auf dem Grafiktyp an, mit dem Sie arbeiten. Wenn Sie unsicher sind und die Gleichung der Linie kennen, stecken Sie die X-Koordinaten wieder in die zu überprüfende Funktion. 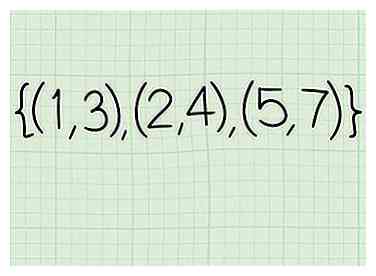 1 Schreiben Sie die Beziehung auf. Eine Beziehung ist nur eine Menge von x- und y-Koordinaten. Nehmen wir an, Sie arbeiten mit den folgenden Koordinaten: (1, 3), (2, 4), (5, 7)
1 Schreiben Sie die Beziehung auf. Eine Beziehung ist nur eine Menge von x- und y-Koordinaten. Nehmen wir an, Sie arbeiten mit den folgenden Koordinaten: (1, 3), (2, 4), (5, 7) 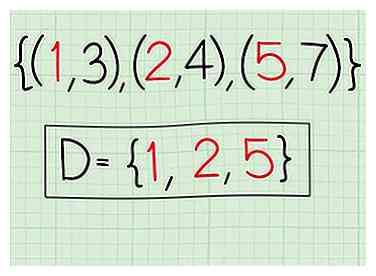 2 Schreiben Sie die x-Koordinaten auf. Sie sind: 1, 2, 5.
2 Schreiben Sie die x-Koordinaten auf. Sie sind: 1, 2, 5. 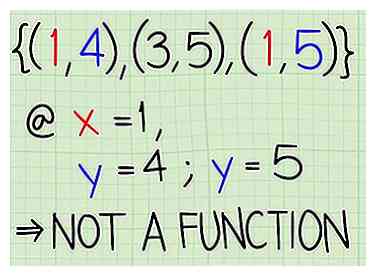 3 Geben Sie die Domäne an. D = 1, 2, 5
3 Geben Sie die Domäne an. D = 1, 2, 5