Ein rechteckiges Prisma ist ein Name für eine 6-seitige 3-dimensionale Figur, die jedem sehr vertraut ist - eine Box. Denken Sie an einen Ziegelstein oder einen Schuhkarton, und Sie wissen genau, was ein rechteckiges Prisma ist. Die Fläche ist die Menge an Platz auf der Außenseite des Objekts. "Wie viel Papier brauche ich, um diese Schuhschachtel zu wickeln" klingt viel weniger kompliziert, aber es ist genau das gleiche mathematische Problem.
Teil eins von zwei:
Die Oberfläche finden
-
 1 Beschriften Sie die Länge, Breite und Höhe Ihres rechteckigen Prismas. Jedes rechteckige Prisma hat eine Länge, eine Breite und eine Höhe. Zeichnen Sie ein Bild des Prismas und schreiben Sie die Symbole l, w, und h neben drei verschiedenen Kanten der Form.
1 Beschriften Sie die Länge, Breite und Höhe Ihres rechteckigen Prismas. Jedes rechteckige Prisma hat eine Länge, eine Breite und eine Höhe. Zeichnen Sie ein Bild des Prismas und schreiben Sie die Symbole l, w, und h neben drei verschiedenen Kanten der Form. - Wenn Sie nicht sicher sind, welche Seiten Sie beschriften sollen, wählen Sie eine beliebige Ecke. Beschrifte die drei Linien, die sich an dieser Ecke treffen.
- Zum Beispiel: Eine Box hat eine Basis, die 3 x 4 Zoll misst, und sie steht 5 Zoll hoch. Die lange Seite der Basis ist 4 Zoll, also l = 4, w = 3, und h = 5.
-
 2 Sieh dir die sechs Seiten des Prismas an. Um die gesamte Oberfläche abzudecken, müssten Sie sechs verschiedene "Gesichter" malen. Denken Sie an jeden einzelnen - oder finden Sie eine Schachtel Müsli und schauen Sie direkt an:
2 Sieh dir die sechs Seiten des Prismas an. Um die gesamte Oberfläche abzudecken, müssten Sie sechs verschiedene "Gesichter" malen. Denken Sie an jeden einzelnen - oder finden Sie eine Schachtel Müsli und schauen Sie direkt an: - Es gibt eine obere und eine untere Fläche. Beide sind gleich groß.[1]
- Es gibt eine Vorder- und eine Rückseite. Beide sind gleich groß.
- Es gibt ein linkes und rechtes Gesicht. Beide sind gleich groß.
- Wenn Sie Schwierigkeiten haben, sich das vorzustellen, schneiden Sie eine Kiste entlang der Kanten auseinander und legen Sie sie aus.[2]
-
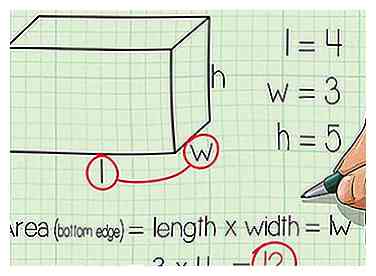 3 Finde den Bereich der unteren Fläche. Fangen wir an, die Oberfläche von nur einer Seite zu finden: die Unterseite. Dies ist ein Rechteck, genau wie jedes Gesicht. Eine Kante des Rechtecks ist als Länge und die andere als Breite bezeichnet. Um die Fläche des Rechtecks zu finden, multiplizieren Sie einfach die beiden Kanten. Fläche (Unterkante) = Länge mal Breite = lw.
3 Finde den Bereich der unteren Fläche. Fangen wir an, die Oberfläche von nur einer Seite zu finden: die Unterseite. Dies ist ein Rechteck, genau wie jedes Gesicht. Eine Kante des Rechtecks ist als Länge und die andere als Breite bezeichnet. Um die Fläche des Rechtecks zu finden, multiplizieren Sie einfach die beiden Kanten. Fläche (Unterkante) = Länge mal Breite = lw. - Zurück zu unserem Beispiel ist der Bereich der unteren Fläche 4 Zoll x 3 Zoll = 12 Quadratzoll.
-
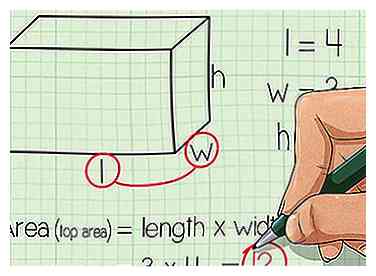 4 Finde den Bereich der oberen Fläche. Warten Sie eine Sekunde - wir haben bereits bemerkt, dass die oberen und unteren Flächen gleich groß sind. Dies muss auch eine Fläche von haben lw.
4 Finde den Bereich der oberen Fläche. Warten Sie eine Sekunde - wir haben bereits bemerkt, dass die oberen und unteren Flächen gleich groß sind. Dies muss auch eine Fläche von haben lw. - In unserem Beispiel ist der obere Bereich auch 12 Quadratzoll.
-
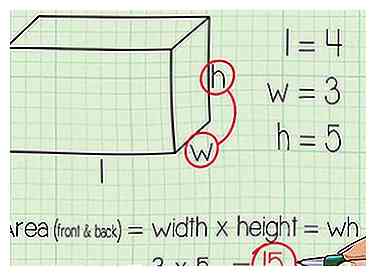 5 Finde die Fläche der Vorder- und Rückseite. Gehen Sie zurück zu Ihrem Diagramm und schauen Sie sich die Vorderseite an: die mit einer Kante, die als Breite und eine als Höhe bezeichnet wird. Die Fläche der Vorderseite = Breite mal Höhe = wh. Der Bereich der Rückseite ist auch wh.
5 Finde die Fläche der Vorder- und Rückseite. Gehen Sie zurück zu Ihrem Diagramm und schauen Sie sich die Vorderseite an: die mit einer Kante, die als Breite und eine als Höhe bezeichnet wird. Die Fläche der Vorderseite = Breite mal Höhe = wh. Der Bereich der Rückseite ist auch wh. - In unserem Beispiel ist w = 3 Zoll und h = 5 Zoll, also ist die Fläche der Vorderseite 3 Zoll x 5 Zoll =15 Quadratzoll. Der Bereich der Rückseite ist auch 15 Quadratzoll.
-
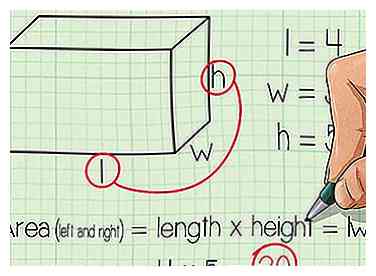 6 Finde die Fläche der linken und rechten Fläche. Wir haben nur noch zwei Gesichter, die alle gleich groß sind. Eine Kante ist die Länge des Prismas und eine Kante ist die Höhe des Prismas. Die Fläche des linken Gesichts ist lh und der Bereich des rechten Gesichts ist auch lh.
6 Finde die Fläche der linken und rechten Fläche. Wir haben nur noch zwei Gesichter, die alle gleich groß sind. Eine Kante ist die Länge des Prismas und eine Kante ist die Höhe des Prismas. Die Fläche des linken Gesichts ist lh und der Bereich des rechten Gesichts ist auch lh. - In unserem Beispiel ist l = 4 Zoll und h = 5 Zoll, also die Fläche der linken Fläche = 4 Zoll × 5 Zoll = 20 Quadratzoll. Die Fläche des rechten Gesichts ist auch 20 Quadratzoll.
-
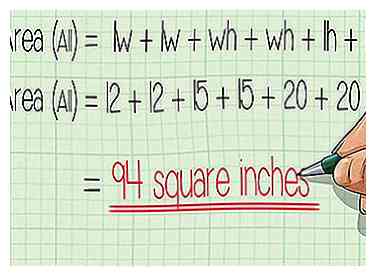 7 Fügen Sie die sechs Bereiche zusammen. Jetzt haben Sie die Fläche jedes der sechs Gesichter gefunden. Fügen Sie sie alle zusammen, um die Fläche der ganzen Form zu erhalten: lw + lw + wh + wh + lh + lh. Sie können diese Formel für jedes rechteckige Prisma verwenden, und Sie erhalten immer die Oberfläche.
7 Fügen Sie die sechs Bereiche zusammen. Jetzt haben Sie die Fläche jedes der sechs Gesichter gefunden. Fügen Sie sie alle zusammen, um die Fläche der ganzen Form zu erhalten: lw + lw + wh + wh + lh + lh. Sie können diese Formel für jedes rechteckige Prisma verwenden, und Sie erhalten immer die Oberfläche. - Um unser Beispiel zu beenden, addieren Sie einfach alle blauen Zahlen oben: 12 + 12 + 15 + 15 + 20 + 20 = 94 Quadratzoll.
Teil zwei von zwei:
Die Formel kürzer machen
-
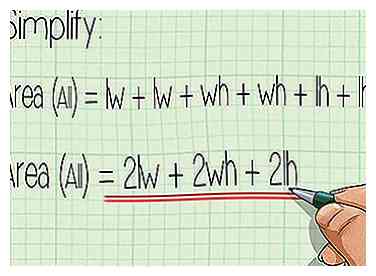 1 Vereinfachen Sie die Formel. Sie wissen jetzt genug, um die Oberfläche eines rechteckigen Prismas zu finden. Sie können es schneller machen, wenn Sie einige grundlegende Algebra gelernt haben. Beginnen Sie mit unserer obigen Gleichung: Fläche eines rechteckigen Prismas = lw + lw + wh + wh + lh + lh. Wenn wir alle Begriffe kombinieren, die gleich sind, erhalten wir:
1 Vereinfachen Sie die Formel. Sie wissen jetzt genug, um die Oberfläche eines rechteckigen Prismas zu finden. Sie können es schneller machen, wenn Sie einige grundlegende Algebra gelernt haben. Beginnen Sie mit unserer obigen Gleichung: Fläche eines rechteckigen Prismas = lw + lw + wh + wh + lh + lh. Wenn wir alle Begriffe kombinieren, die gleich sind, erhalten wir: - Fläche eines rechteckigen Prismas = 2lw + 2wh + 2lh
-
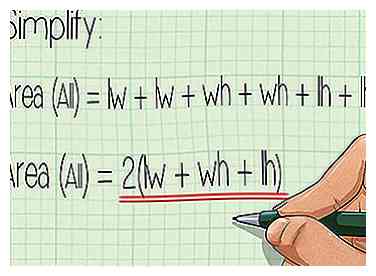 2 Faktor die beiden aus. Wenn Sie Algebra berücksichtigen können, können Sie es noch kürzer machen:
2 Faktor die beiden aus. Wenn Sie Algebra berücksichtigen können, können Sie es noch kürzer machen: - Fläche eines rechteckigen Prismas = 2lw + 2wh + 2lh = 2 (lw + wh + lh).
-
 3 Testen Sie es an einem Beispiel. Gehen wir zurück zu unserer Beispiel-Box mit den Längen 4, 3 und 5. Fügen Sie diese Zahlen in die Formel ein:
3 Testen Sie es an einem Beispiel. Gehen wir zurück zu unserer Beispiel-Box mit den Längen 4, 3 und 5. Fügen Sie diese Zahlen in die Formel ein: - Fläche = 2 (lw + wh + lh) = 2 × (lw + wh + lh) = 2 × (4 × 3 + 3 × 5 + 4 × 5) = 2 × (12 + 15 + 20) = 2 × (47) = 94 Quadratzoll . Das ist die gleiche Antwort wie zuvor. Sobald Sie diese Gleichungen geübt haben, können Sie die Oberfläche viel schneller finden.
Oberflächenhilfe
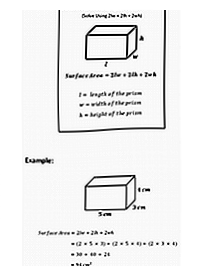 Oberfläche eines rechteckigen Prismas unter Verwendung von Spickzettel
Oberfläche eines rechteckigen Prismas unter Verwendung von Spickzettel  Oberfläche eines rechteckigen Prismas mit Flächenschummel
Oberfläche eines rechteckigen Prismas mit Flächenschummel  Oberfläche eines rechteckigen Prisma-Rechners
Oberfläche eines rechteckigen Prisma-Rechners
 Minotauromaquia
Minotauromaquia
 1 Beschriften Sie die Länge, Breite und Höhe Ihres rechteckigen Prismas. Jedes rechteckige Prisma hat eine Länge, eine Breite und eine Höhe. Zeichnen Sie ein Bild des Prismas und schreiben Sie die Symbole l, w, und h neben drei verschiedenen Kanten der Form.
1 Beschriften Sie die Länge, Breite und Höhe Ihres rechteckigen Prismas. Jedes rechteckige Prisma hat eine Länge, eine Breite und eine Höhe. Zeichnen Sie ein Bild des Prismas und schreiben Sie die Symbole l, w, und h neben drei verschiedenen Kanten der Form.  2 Sieh dir die sechs Seiten des Prismas an. Um die gesamte Oberfläche abzudecken, müssten Sie sechs verschiedene "Gesichter" malen. Denken Sie an jeden einzelnen - oder finden Sie eine Schachtel Müsli und schauen Sie direkt an:
2 Sieh dir die sechs Seiten des Prismas an. Um die gesamte Oberfläche abzudecken, müssten Sie sechs verschiedene "Gesichter" malen. Denken Sie an jeden einzelnen - oder finden Sie eine Schachtel Müsli und schauen Sie direkt an:  3 Finde den Bereich der unteren Fläche. Fangen wir an, die Oberfläche von nur einer Seite zu finden: die Unterseite. Dies ist ein Rechteck, genau wie jedes Gesicht. Eine Kante des Rechtecks ist als Länge und die andere als Breite bezeichnet. Um die Fläche des Rechtecks zu finden, multiplizieren Sie einfach die beiden Kanten. Fläche (Unterkante) = Länge mal Breite = lw.
3 Finde den Bereich der unteren Fläche. Fangen wir an, die Oberfläche von nur einer Seite zu finden: die Unterseite. Dies ist ein Rechteck, genau wie jedes Gesicht. Eine Kante des Rechtecks ist als Länge und die andere als Breite bezeichnet. Um die Fläche des Rechtecks zu finden, multiplizieren Sie einfach die beiden Kanten. Fläche (Unterkante) = Länge mal Breite = lw.  4 Finde den Bereich der oberen Fläche. Warten Sie eine Sekunde - wir haben bereits bemerkt, dass die oberen und unteren Flächen gleich groß sind. Dies muss auch eine Fläche von haben lw.
4 Finde den Bereich der oberen Fläche. Warten Sie eine Sekunde - wir haben bereits bemerkt, dass die oberen und unteren Flächen gleich groß sind. Dies muss auch eine Fläche von haben lw.  5 Finde die Fläche der Vorder- und Rückseite. Gehen Sie zurück zu Ihrem Diagramm und schauen Sie sich die Vorderseite an: die mit einer Kante, die als Breite und eine als Höhe bezeichnet wird. Die Fläche der Vorderseite = Breite mal Höhe = wh. Der Bereich der Rückseite ist auch wh.
5 Finde die Fläche der Vorder- und Rückseite. Gehen Sie zurück zu Ihrem Diagramm und schauen Sie sich die Vorderseite an: die mit einer Kante, die als Breite und eine als Höhe bezeichnet wird. Die Fläche der Vorderseite = Breite mal Höhe = wh. Der Bereich der Rückseite ist auch wh.  6 Finde die Fläche der linken und rechten Fläche. Wir haben nur noch zwei Gesichter, die alle gleich groß sind. Eine Kante ist die Länge des Prismas und eine Kante ist die Höhe des Prismas. Die Fläche des linken Gesichts ist lh und der Bereich des rechten Gesichts ist auch lh.
6 Finde die Fläche der linken und rechten Fläche. Wir haben nur noch zwei Gesichter, die alle gleich groß sind. Eine Kante ist die Länge des Prismas und eine Kante ist die Höhe des Prismas. Die Fläche des linken Gesichts ist lh und der Bereich des rechten Gesichts ist auch lh. 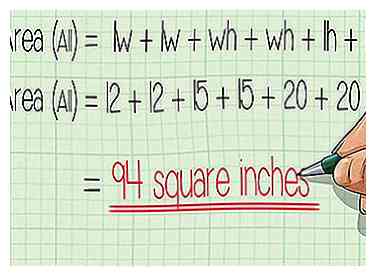 7 Fügen Sie die sechs Bereiche zusammen. Jetzt haben Sie die Fläche jedes der sechs Gesichter gefunden. Fügen Sie sie alle zusammen, um die Fläche der ganzen Form zu erhalten: lw + lw + wh + wh + lh + lh. Sie können diese Formel für jedes rechteckige Prisma verwenden, und Sie erhalten immer die Oberfläche.
7 Fügen Sie die sechs Bereiche zusammen. Jetzt haben Sie die Fläche jedes der sechs Gesichter gefunden. Fügen Sie sie alle zusammen, um die Fläche der ganzen Form zu erhalten: lw + lw + wh + wh + lh + lh. Sie können diese Formel für jedes rechteckige Prisma verwenden, und Sie erhalten immer die Oberfläche. 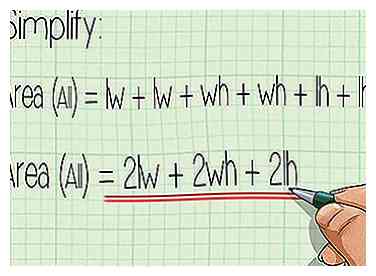 1 Vereinfachen Sie die Formel. Sie wissen jetzt genug, um die Oberfläche eines rechteckigen Prismas zu finden. Sie können es schneller machen, wenn Sie einige grundlegende Algebra gelernt haben. Beginnen Sie mit unserer obigen Gleichung: Fläche eines rechteckigen Prismas = lw + lw + wh + wh + lh + lh. Wenn wir alle Begriffe kombinieren, die gleich sind, erhalten wir:
1 Vereinfachen Sie die Formel. Sie wissen jetzt genug, um die Oberfläche eines rechteckigen Prismas zu finden. Sie können es schneller machen, wenn Sie einige grundlegende Algebra gelernt haben. Beginnen Sie mit unserer obigen Gleichung: Fläche eines rechteckigen Prismas = lw + lw + wh + wh + lh + lh. Wenn wir alle Begriffe kombinieren, die gleich sind, erhalten wir: 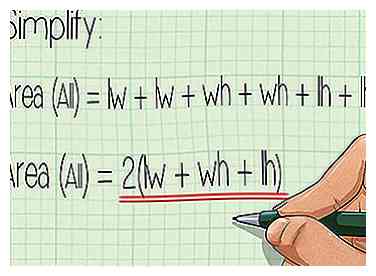 2 Faktor die beiden aus. Wenn Sie Algebra berücksichtigen können, können Sie es noch kürzer machen:
2 Faktor die beiden aus. Wenn Sie Algebra berücksichtigen können, können Sie es noch kürzer machen:  3 Testen Sie es an einem Beispiel. Gehen wir zurück zu unserer Beispiel-Box mit den Längen 4, 3 und 5. Fügen Sie diese Zahlen in die Formel ein:
3 Testen Sie es an einem Beispiel. Gehen wir zurück zu unserer Beispiel-Box mit den Längen 4, 3 und 5. Fügen Sie diese Zahlen in die Formel ein: