Anders als bei einer geraden Linie ändert sich die Steigung einer Kurve ständig, wenn Sie sich entlang der Grafik bewegen. Die Analysis führt die Schüler auf die Idee ein, dass jeder Punkt in diesem Graphen mit einer Steigung oder einer "augenblicklichen Änderungsrate" beschrieben werden könnte. Die Tangente ist eine gerade Linie mit dieser Steigung, die durch den genauen Punkt im Diagramm verläuft. Um die Gleichung für die Tangente zu finden, müssen Sie wissen, wie Sie die Ableitung der ursprünglichen Gleichung berechnen können.
Methode eins von zwei:
Die Gleichung einer Tangentenlinie finden
-
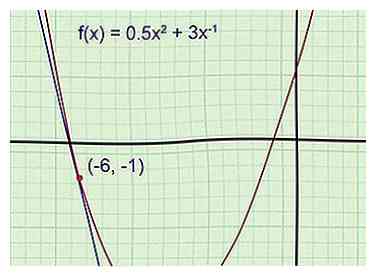 1 Skizzieren Sie die Funktion und die Tangente (empfohlen). Ein Graph erleichtert es, dem Problem zu folgen und zu prüfen, ob die Antwort sinnvoll ist. Skizzieren Sie die Funktion auf einem Millimeterpapier und verwenden Sie bei Bedarf einen grafischen Rechner als Referenz. Skizzieren Sie die Tangente durch den gegebenen Punkt. (Denken Sie daran, dass die Tangente durch diesen Punkt verläuft und dieselbe Neigung wie der Graph an diesem Punkt aufweist.)
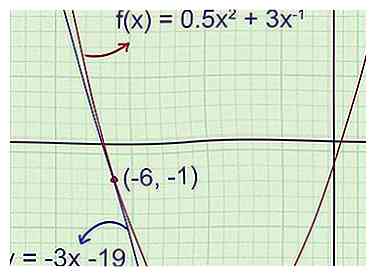
1 Skizzieren Sie die Funktion und die Tangente (empfohlen). Ein Graph erleichtert es, dem Problem zu folgen und zu prüfen, ob die Antwort sinnvoll ist. Skizzieren Sie die Funktion auf einem Millimeterpapier und verwenden Sie bei Bedarf einen grafischen Rechner als Referenz. Skizzieren Sie die Tangente durch den gegebenen Punkt. (Denken Sie daran, dass die Tangente durch diesen Punkt verläuft und dieselbe Neigung wie der Graph an diesem Punkt aufweist.) - Beispiel 1: Skizzieren Sie das Diagramm der Parabel . Zeichnen Sie den durchgehenden Tangentenpunkt (-6, -1).
Sie kennen die Tangentengleichung noch nicht, aber Sie können bereits sagen, dass ihre Steigung negativ ist und dass ihr y-Achsenabschnitt negativ ist (deutlich unterhalb des Parabolscheitelpunkts mit y-Wert -5.5). Wenn Ihre endgültige Antwort nicht mit diesen Details übereinstimmt, werden Sie Ihre Arbeit auf Fehler überprüfen.
- Beispiel 1: Skizzieren Sie das Diagramm der Parabel . Zeichnen Sie den durchgehenden Tangentenpunkt (-6, -1).
-
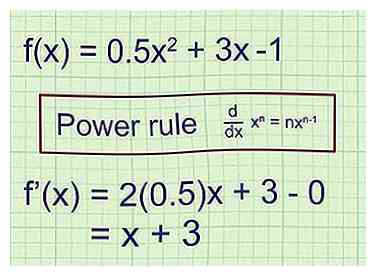 2 Nimm die erste Ableitung, um die Gleichung für die Gleichung zu finden Steigung der Tangente. Für die Funktion f (x) repräsentiert die erste Ableitung f '(x) die Gleichung für die Steigung der Tangente an irgendeinem Punkt auf f (x). Es gibt viele Möglichkeiten, Derivate zu verwenden. Hier ist ein einfaches Beispiel mit der Potenzregel:[1]
2 Nimm die erste Ableitung, um die Gleichung für die Gleichung zu finden Steigung der Tangente. Für die Funktion f (x) repräsentiert die erste Ableitung f '(x) die Gleichung für die Steigung der Tangente an irgendeinem Punkt auf f (x). Es gibt viele Möglichkeiten, Derivate zu verwenden. Hier ist ein einfaches Beispiel mit der Potenzregel:[1] - Beispiel 1 (Fortsetzung): Die Grafik wird durch die Funktion beschrieben .
Rufen Sie die Potenzregel beim Ableiten von Derivaten auf: .
Die erste Ableitung der Funktion = f '(x) = (2) (0,5) x + 3 - 0.
f '(x) = x + 3. Schließen Sie einen beliebigen Wert a für x in diese Gleichung ein, und das Ergebnis ist die Steigung der Tangente an f (x) an dem Punkt, an dem x = a ist.
- Beispiel 1 (Fortsetzung): Die Grafik wird durch die Funktion beschrieben .
-
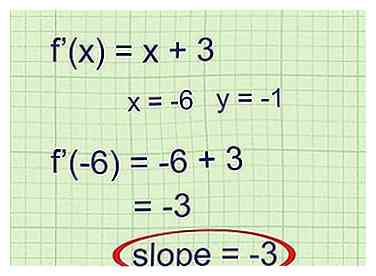 3 Geben Sie den x-Wert des zu untersuchenden Punktes ein. Lesen Sie das Problem, um die Koordinaten des Punkts zu ermitteln, für den Sie die Tangente finden. Geben Sie die x-Koordinate dieses Punktes in f '(x) ein. Die Ausgabe ist die Steigung der Tangente an diesem Punkt.
3 Geben Sie den x-Wert des zu untersuchenden Punktes ein. Lesen Sie das Problem, um die Koordinaten des Punkts zu ermitteln, für den Sie die Tangente finden. Geben Sie die x-Koordinate dieses Punktes in f '(x) ein. Die Ausgabe ist die Steigung der Tangente an diesem Punkt. - Beispiel 1 (Fortsetzung): Der in dem Problem erwähnte Punkt ist (-6, -1). Verwenden Sie die x-Koordinate -6 als Eingabe für f '(x):
f '(- 6) = -6 + 3 = -3
Die Steigung der Tangente ist -3.
- Beispiel 1 (Fortsetzung): Der in dem Problem erwähnte Punkt ist (-6, -1). Verwenden Sie die x-Koordinate -6 als Eingabe für f '(x):
-
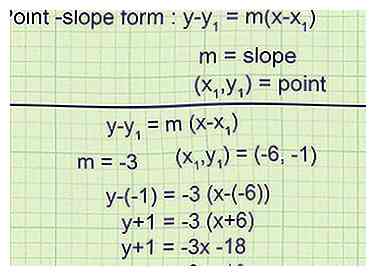 4 Schreiben Sie die Tangentengleichung in Punkt-Steigung-Form. Die Punktneigungsform einer linearen Gleichung ist , woher m ist die Steigung und ist ein Punkt auf der Linie.[2] Sie haben jetzt alle Informationen, die Sie benötigen, um die Gleichung der Tangente in dieser Form zu schreiben.
4 Schreiben Sie die Tangentengleichung in Punkt-Steigung-Form. Die Punktneigungsform einer linearen Gleichung ist , woher m ist die Steigung und ist ein Punkt auf der Linie.[2] Sie haben jetzt alle Informationen, die Sie benötigen, um die Gleichung der Tangente in dieser Form zu schreiben. - Beispiel 1 (Fortsetzung):
Die Steigung der Linie beträgt -3
Die Tangente verläuft durch (-6, -1), also ist die endgültige Gleichung
Vereinfachen zu
- Beispiel 1 (Fortsetzung):
-
 5 Bestätigen Sie die Gleichung in Ihrem Diagramm. Wenn Sie einen Grafikrechner haben, zeichnen Sie die Originalfunktion und die Tangente, um zu überprüfen, ob Sie die richtige Antwort haben. Wenn Sie auf Papier arbeiten, finden Sie in Ihrer früheren Grafik sicher, dass Ihre Antwort keine eklatanten Fehler enthält.
5 Bestätigen Sie die Gleichung in Ihrem Diagramm. Wenn Sie einen Grafikrechner haben, zeichnen Sie die Originalfunktion und die Tangente, um zu überprüfen, ob Sie die richtige Antwort haben. Wenn Sie auf Papier arbeiten, finden Sie in Ihrer früheren Grafik sicher, dass Ihre Antwort keine eklatanten Fehler enthält. - Beispiel 1 (Fortsetzung): Die anfängliche Skizze zeigte, dass die Steigung der Tangente negativ war und der y-Schnitt deutlich unter -5,5 lag. Die Tangentengleichung, die wir gefunden haben, ist y = -3x - 19 in der Form des Steigungsintercepts, was bedeutet, dass -3 die Steigung und -19 der y-Achsenabschnitt ist. Beide Attribute stimmen mit den anfänglichen Vorhersagen überein.
-
 6 Versuchen Sie ein schwierigeres Problem. Hier ist wieder ein Durchlauf des gesamten Prozesses. Dieses Mal ist es das Ziel, die Tangente an die Tangente zu finden bei x = 2:
6 Versuchen Sie ein schwierigeres Problem. Hier ist wieder ein Durchlauf des gesamten Prozesses. Dieses Mal ist es das Ziel, die Tangente an die Tangente zu finden bei x = 2: - Unter Verwendung der Potenzregel die erste Ableitung . Diese Funktion sagt uns die Steigung der Tangente.
- Da x = 2, finde . Dies ist die Steigung bei x = 2.
- Beachten Sie, dass wir diesmal keinen Punkt haben, nur eine x-Koordinate. Um die y-Koordinate zu finden, stecke x = 2 in die Anfangsfunktion: . Der Punkt ist (2,27).
- Schreiben Sie die Tangentengleichung in Punkt-Steigung-Form:
Falls erforderlich, vereinfachen Sie auf y = 25x - 23.
Methode zwei von zwei:
Verwandte Probleme lösen
-
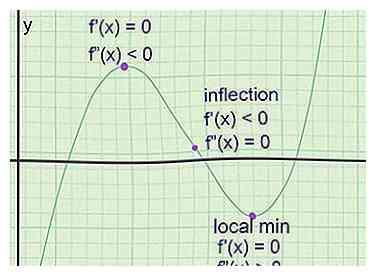 1 Finde die Extrempunkte in einem Graphen. Dies sind Punkte, an denen der Graph ein lokales Maximum erreicht (ein Punkt höher als die Punkte auf jeder Seite), oder ein lokales Minimum (niedriger als die Punkte auf jeder Seite). Die Tangente hat an diesen Punkten immer eine Steigung von 0 (eine horizontale Linie), aber eine Steigung von Null alleine garantiert keinen extremen Punkt. So finden Sie sie:[3]
1 Finde die Extrempunkte in einem Graphen. Dies sind Punkte, an denen der Graph ein lokales Maximum erreicht (ein Punkt höher als die Punkte auf jeder Seite), oder ein lokales Minimum (niedriger als die Punkte auf jeder Seite). Die Tangente hat an diesen Punkten immer eine Steigung von 0 (eine horizontale Linie), aber eine Steigung von Null alleine garantiert keinen extremen Punkt. So finden Sie sie:[3] - Nehmen Sie die erste Ableitung der Funktion, um f '(x) zu erhalten, die Gleichung für die Steigung der Tangente.
- Löse für f '(x) = 0, um zu finden möglich extreme Punkte.
- Nehmen Sie die zweite Ableitung, um f "(x) zu erhalten, die Gleichung, die Ihnen sagt, wie schnell sich die Steigung der Tangente ändert.
- Fügen Sie für jeden möglichen Extrempunkt die X-Koordinate ein ein in f "(x). Wenn f" (a) positiv ist, gibt es ein lokales Minimum bei ein. Wenn f "(a) negativ ist, gibt es ein lokales Maximum. Wenn f" (a) 0 ist, gibt es einen Wendepunkt, keinen Extrempunkt.
- Wenn es ein Maximum oder Minimum bei gibt ein, finde f (a), um die y-Koordinate zu erhalten.
-
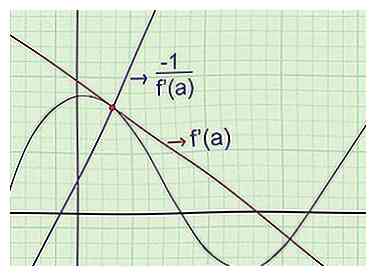 2 Finde die Gleichung des Normalen. Die "Normale" zu einer Kurve an einem bestimmten Punkt verläuft durch diesen Punkt, hat jedoch eine Neigung senkrecht zu einer Tangente. Um die Gleichung für die Normale zu finden, nutzen Sie die Tatsache, dass (Steigung der Tangente) (Steigung der Normalen) = -1, wenn sie beide durch den gleichen Punkt in der Grafik gehen.[4] Mit anderen Worten:
2 Finde die Gleichung des Normalen. Die "Normale" zu einer Kurve an einem bestimmten Punkt verläuft durch diesen Punkt, hat jedoch eine Neigung senkrecht zu einer Tangente. Um die Gleichung für die Normale zu finden, nutzen Sie die Tatsache, dass (Steigung der Tangente) (Steigung der Normalen) = -1, wenn sie beide durch den gleichen Punkt in der Grafik gehen.[4] Mit anderen Worten: - Finde f '(x), die Steigung der Tangente.
- Wenn der Punkt bei x = ist einFinden Sie f '(a), um die Steigung der Tangente an diesem Punkt zu finden.
- Berechnung um die Steigung der Normalen zu finden.
- Schreibe die normale Gleichung in Form eines Anstiegs.
 Minotauromaquia
Minotauromaquia
 1 Skizzieren Sie die Funktion und die Tangente (empfohlen). Ein Graph erleichtert es, dem Problem zu folgen und zu prüfen, ob die Antwort sinnvoll ist. Skizzieren Sie die Funktion auf einem Millimeterpapier und verwenden Sie bei Bedarf einen grafischen Rechner als Referenz. Skizzieren Sie die Tangente durch den gegebenen Punkt. (Denken Sie daran, dass die Tangente durch diesen Punkt verläuft und dieselbe Neigung wie der Graph an diesem Punkt aufweist.)
1 Skizzieren Sie die Funktion und die Tangente (empfohlen). Ein Graph erleichtert es, dem Problem zu folgen und zu prüfen, ob die Antwort sinnvoll ist. Skizzieren Sie die Funktion auf einem Millimeterpapier und verwenden Sie bei Bedarf einen grafischen Rechner als Referenz. Skizzieren Sie die Tangente durch den gegebenen Punkt. (Denken Sie daran, dass die Tangente durch diesen Punkt verläuft und dieselbe Neigung wie der Graph an diesem Punkt aufweist.) 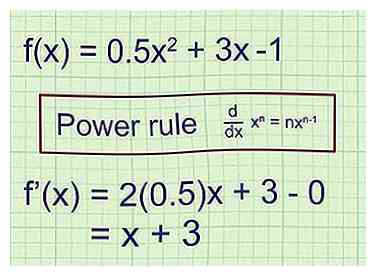 2 Nimm die erste Ableitung, um die Gleichung für die Gleichung zu finden Steigung der Tangente. Für die Funktion f (x) repräsentiert die erste Ableitung f '(x) die Gleichung für die Steigung der Tangente an irgendeinem Punkt auf f (x). Es gibt viele Möglichkeiten, Derivate zu verwenden. Hier ist ein einfaches Beispiel mit der Potenzregel:[1]
2 Nimm die erste Ableitung, um die Gleichung für die Gleichung zu finden Steigung der Tangente. Für die Funktion f (x) repräsentiert die erste Ableitung f '(x) die Gleichung für die Steigung der Tangente an irgendeinem Punkt auf f (x). Es gibt viele Möglichkeiten, Derivate zu verwenden. Hier ist ein einfaches Beispiel mit der Potenzregel:[1] 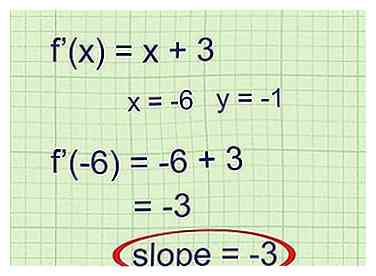 3 Geben Sie den x-Wert des zu untersuchenden Punktes ein. Lesen Sie das Problem, um die Koordinaten des Punkts zu ermitteln, für den Sie die Tangente finden. Geben Sie die x-Koordinate dieses Punktes in f '(x) ein. Die Ausgabe ist die Steigung der Tangente an diesem Punkt.
3 Geben Sie den x-Wert des zu untersuchenden Punktes ein. Lesen Sie das Problem, um die Koordinaten des Punkts zu ermitteln, für den Sie die Tangente finden. Geben Sie die x-Koordinate dieses Punktes in f '(x) ein. Die Ausgabe ist die Steigung der Tangente an diesem Punkt. 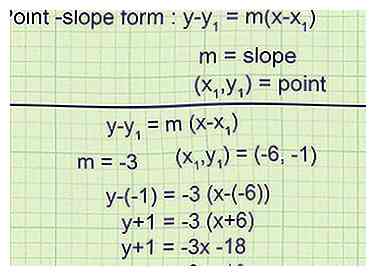 4 Schreiben Sie die Tangentengleichung in Punkt-Steigung-Form. Die Punktneigungsform einer linearen Gleichung ist
4 Schreiben Sie die Tangentengleichung in Punkt-Steigung-Form. Die Punktneigungsform einer linearen Gleichung ist  5 Bestätigen Sie die Gleichung in Ihrem Diagramm. Wenn Sie einen Grafikrechner haben, zeichnen Sie die Originalfunktion und die Tangente, um zu überprüfen, ob Sie die richtige Antwort haben. Wenn Sie auf Papier arbeiten, finden Sie in Ihrer früheren Grafik sicher, dass Ihre Antwort keine eklatanten Fehler enthält.
5 Bestätigen Sie die Gleichung in Ihrem Diagramm. Wenn Sie einen Grafikrechner haben, zeichnen Sie die Originalfunktion und die Tangente, um zu überprüfen, ob Sie die richtige Antwort haben. Wenn Sie auf Papier arbeiten, finden Sie in Ihrer früheren Grafik sicher, dass Ihre Antwort keine eklatanten Fehler enthält.  6 Versuchen Sie ein schwierigeres Problem. Hier ist wieder ein Durchlauf des gesamten Prozesses. Dieses Mal ist es das Ziel, die Tangente an die Tangente zu finden
6 Versuchen Sie ein schwierigeres Problem. Hier ist wieder ein Durchlauf des gesamten Prozesses. Dieses Mal ist es das Ziel, die Tangente an die Tangente zu finden  1 Finde die Extrempunkte in einem Graphen. Dies sind Punkte, an denen der Graph ein lokales Maximum erreicht (ein Punkt höher als die Punkte auf jeder Seite), oder ein lokales Minimum (niedriger als die Punkte auf jeder Seite). Die Tangente hat an diesen Punkten immer eine Steigung von 0 (eine horizontale Linie), aber eine Steigung von Null alleine garantiert keinen extremen Punkt. So finden Sie sie:[3]
1 Finde die Extrempunkte in einem Graphen. Dies sind Punkte, an denen der Graph ein lokales Maximum erreicht (ein Punkt höher als die Punkte auf jeder Seite), oder ein lokales Minimum (niedriger als die Punkte auf jeder Seite). Die Tangente hat an diesen Punkten immer eine Steigung von 0 (eine horizontale Linie), aber eine Steigung von Null alleine garantiert keinen extremen Punkt. So finden Sie sie:[3]  2 Finde die Gleichung des Normalen. Die "Normale" zu einer Kurve an einem bestimmten Punkt verläuft durch diesen Punkt, hat jedoch eine Neigung senkrecht zu einer Tangente. Um die Gleichung für die Normale zu finden, nutzen Sie die Tatsache, dass (Steigung der Tangente) (Steigung der Normalen) = -1, wenn sie beide durch den gleichen Punkt in der Grafik gehen.[4] Mit anderen Worten:
2 Finde die Gleichung des Normalen. Die "Normale" zu einer Kurve an einem bestimmten Punkt verläuft durch diesen Punkt, hat jedoch eine Neigung senkrecht zu einer Tangente. Um die Gleichung für die Normale zu finden, nutzen Sie die Tatsache, dass (Steigung der Tangente) (Steigung der Normalen) = -1, wenn sie beide durch den gleichen Punkt in der Grafik gehen.[4] Mit anderen Worten: