Perimeter ist ein Maß für die Fläche oder den Abstand um eine zweidimensionale Form. Bei einem Rechteck ist der Umfang beispielsweise die Gesamtlänge des Umrisses des Rechtecks, einschließlich der beiden Breitenbegrenzungen und der beiden Längsränder. Um den Umfang einer Form zu bestimmen, fügen Sie daher alle Dimensionen hinzu, aus denen die äußere Kante der Form besteht. Die Möglichkeit, den Umfang einer Form zu finden, hat viele Anwendungen in der realen Welt. Sagen Sie zum Beispiel, dass Sie einen Zaun um Ihren Hinterhof bauen wollten. Um Materialien zu kaufen, müssen Sie wissen, wie viel Zaun Sie benötigen, und um festzustellen, dass Sie den Umfang des Bereichs, den Sie eingrenzen möchten, herausfinden müssen.
Teil eins von zwei:
Den Umfang der meisten Formen finden
-
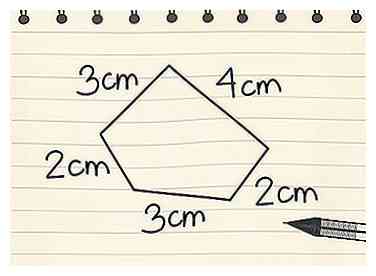 1 Bestimmen Sie die Länge jeder Seite. Da der Umfang nur ein Maß für den Umriss einer zweidimensionalen Figur ist, benötigen Sie normalerweise keine spezielle Formel, um den Umfang zu finden (obwohl es Gleichungen für bestimmte Formen gibt, um es einfacher zu machen). Sie müssen jedoch die Länge aller Seiten der Form kennen.[1]
1 Bestimmen Sie die Länge jeder Seite. Da der Umfang nur ein Maß für den Umriss einer zweidimensionalen Figur ist, benötigen Sie normalerweise keine spezielle Formel, um den Umfang zu finden (obwohl es Gleichungen für bestimmte Formen gibt, um es einfacher zu machen). Sie müssen jedoch die Länge aller Seiten der Form kennen.[1] - Zum Beispiel hat ein Fünfeck fünf Seiten, und Sie müssen die Länge jedes einzelnen wissen, um den Umfang zu bestimmen.
- Selbst mit einem unregelmäßigen Polygon, das 20 Seiten hat, können Sie immer noch den Umfang finden, solange Sie die Länge jeder Seite kennen.
-
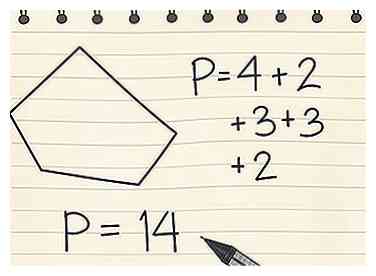 2 Fügen Sie die Länge aller Seiten zusammen. Um den Umfang von nicht kreisförmigen Objekten zu finden, ermitteln Sie die Summe aller Seitenlängen, um den Abstand um die Form zu bestimmen.[2]
2 Fügen Sie die Länge aller Seiten zusammen. Um den Umfang von nicht kreisförmigen Objekten zu finden, ermitteln Sie die Summe aller Seitenlängen, um den Abstand um die Form zu bestimmen.[2] - Nehmen wir an, das unregelmäßige Fünfeck hat die folgenden Längen: A = 4, B = 2, C = 3, D = 3 und E = 2
- Füge 4 + 2 + 3 + 3 + 2 = 14 hinzu, wobei P (Umfang) = 14 ist
-
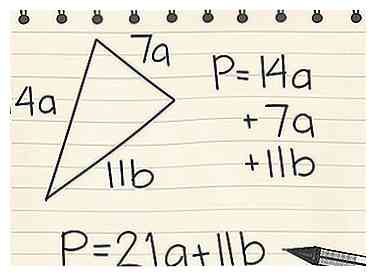 3 Umgang mit Variablen. Sie können Perimeter immer noch finden, wenn Sie mit Variablen arbeiten. Angenommen, Sie haben ein Dreieck mit den Seitenlängen 14a, 11b und 7a:[3]
3 Umgang mit Variablen. Sie können Perimeter immer noch finden, wenn Sie mit Variablen arbeiten. Angenommen, Sie haben ein Dreieck mit den Seitenlängen 14a, 11b und 7a:[3] - Finde die Summe aller Seiten: P = 14a + 11b + 7a
- Kombiniere die gleichen Ausdrücke: P = (14a + 7a) + 11b
- P = 21a + 11b
-
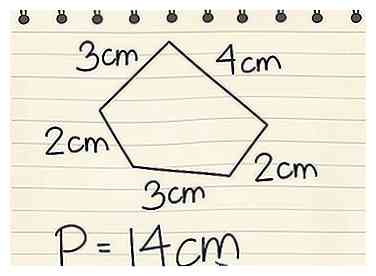 4 Achten Sie auf Maßeinheiten. In einer realen Anwendung reicht es nicht aus, den Umfang eines Objekts zu finden, wenn Sie nicht wissen, mit welcher Maßeinheit Sie arbeiten (z. B. Fuß, Kilometer oder Meter). Wenn mit dem Fünfeck jede Seite in Zentimetern gemessen wurde, dann wissen Sie, dass P = 14 cm ist.
4 Achten Sie auf Maßeinheiten. In einer realen Anwendung reicht es nicht aus, den Umfang eines Objekts zu finden, wenn Sie nicht wissen, mit welcher Maßeinheit Sie arbeiten (z. B. Fuß, Kilometer oder Meter). Wenn mit dem Fünfeck jede Seite in Zentimetern gemessen wurde, dann wissen Sie, dass P = 14 cm ist.
Teil zwei von zwei:
Perimeter-Formeln lernen
-
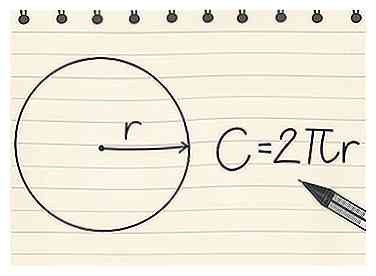 1 Finde den Umfang eines Kreises. Einige reguläre Formen haben Formeln, die es schneller machen, den Umfang der Figur zu finden. Aber es gibt andere Formen wie Kreise, die eine Formel benötigen, um den Umfang zu finden. Der Umfang eines Kreises wird Umfang genannt. Um den Umfang eines Kreises zu finden, verwenden Sie die Gleichung C (Umfang) = 2πr.[4]
1 Finde den Umfang eines Kreises. Einige reguläre Formen haben Formeln, die es schneller machen, den Umfang der Figur zu finden. Aber es gibt andere Formen wie Kreise, die eine Formel benötigen, um den Umfang zu finden. Der Umfang eines Kreises wird Umfang genannt. Um den Umfang eines Kreises zu finden, verwenden Sie die Gleichung C (Umfang) = 2πr.[4] - Um zu beginnen, suchen Sie den Radius des Kreises, der die Länge eines Liniensegments darstellt, das von der Mitte des Kreises bis zum Umfang verläuft.
- Verwenden Sie für einfachere Gleichungen die verkürzte Version π = 3.14
- Für einen Kreis mit einem Radius von 4 cm: C = 2 x 3,14 x 4 = 25,12 cm
-
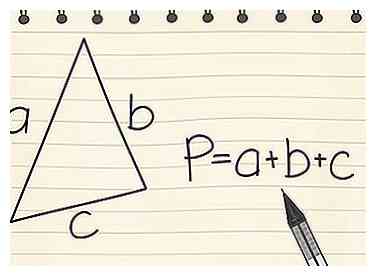 2 Finde den Umfang eines Dreiecks. Verwenden Sie die Gleichung P = a + b + c für ein Dreieck. Wenn beispielsweise ein Dreieck die Abmessungen a = 20 cm, b = 11 cm und c = 9 cm hat, dann ist P = 20 + 11 + 9 = 40 cm.
2 Finde den Umfang eines Dreiecks. Verwenden Sie die Gleichung P = a + b + c für ein Dreieck. Wenn beispielsweise ein Dreieck die Abmessungen a = 20 cm, b = 11 cm und c = 9 cm hat, dann ist P = 20 + 11 + 9 = 40 cm. -
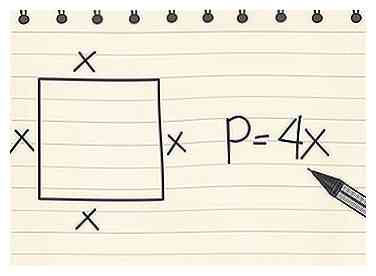 3 Finde den Umfang eines Quadrats. Da ein Quadrat vier Seiten gleicher Länge hat, können Sie die einfache Gleichung P = 4x verwenden, wobei x der Länge einer Seite entspricht.
3 Finde den Umfang eines Quadrats. Da ein Quadrat vier Seiten gleicher Länge hat, können Sie die einfache Gleichung P = 4x verwenden, wobei x der Länge einer Seite entspricht. - Auf einem Quadrat mit x = 3 cm, dann P = 4 x 3 = 12 cm
-
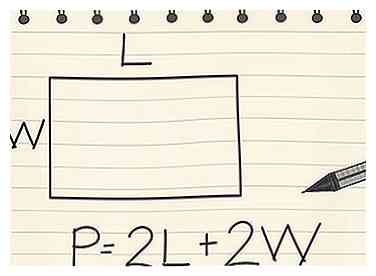 4 Finde den Umfang eines Rechtecks. Da die Längsseiten die gleichen sind und die Breitenseiten auf einem Rechteck gleich sind, können Sie die Gleichung P = 2l + 2w verwenden, wobei l die Länge einer Seite und w die Breite einer Seite ist. Für ein Rechteck mit l = 8cm und w = 5cm:
4 Finde den Umfang eines Rechtecks. Da die Längsseiten die gleichen sind und die Breitenseiten auf einem Rechteck gleich sind, können Sie die Gleichung P = 2l + 2w verwenden, wobei l die Länge einer Seite und w die Breite einer Seite ist. Für ein Rechteck mit l = 8cm und w = 5cm: - P = (2 x 8) + (2 x 5)
- P = 16 + 10
- P = 26 cm
- Die Gleichung P = 2 (l + h) gibt Ihnen auch das gleiche Ergebnis: 2 (8 + 5) = 2 (13) = 26 cm[5]
-
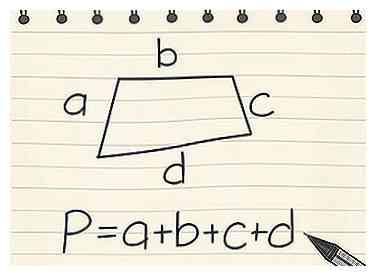 5 Finde den Umfang anderer Vierecke. Ein Viereck bezieht sich auf jede zweidimensionale Form mit vier geschlossenen, geraden Seiten. Dazu gehören Rechtecke, Quadrate, Trapeze, Parallelogramme, Drachen und Rhomben.[6] Je nach den Seiten gibt es drei Gleichungen für ein Viereck:
5 Finde den Umfang anderer Vierecke. Ein Viereck bezieht sich auf jede zweidimensionale Form mit vier geschlossenen, geraden Seiten. Dazu gehören Rechtecke, Quadrate, Trapeze, Parallelogramme, Drachen und Rhomben.[6] Je nach den Seiten gibt es drei Gleichungen für ein Viereck: - Für ein Viereck ohne gleiche Seiten, wie ein unregelmäßiges Trapez, verwenden Sie die Gleichung P = a + b + c + d
- Verwenden Sie für ein Viereck mit vier gleichen Seiten dieselbe Gleichung wie ein Quadrat: P = 4x.
- Für Vierecke, bei denen die Längsseiten gleich sind und die Breitenseiten gleich sind (wie ein Rechteck), verwenden Sie die Gleichungen P = 2a + 2b oder P = 2 (a + b)
 Minotauromaquia
Minotauromaquia
 1 Bestimmen Sie die Länge jeder Seite. Da der Umfang nur ein Maß für den Umriss einer zweidimensionalen Figur ist, benötigen Sie normalerweise keine spezielle Formel, um den Umfang zu finden (obwohl es Gleichungen für bestimmte Formen gibt, um es einfacher zu machen). Sie müssen jedoch die Länge aller Seiten der Form kennen.[1]
1 Bestimmen Sie die Länge jeder Seite. Da der Umfang nur ein Maß für den Umriss einer zweidimensionalen Figur ist, benötigen Sie normalerweise keine spezielle Formel, um den Umfang zu finden (obwohl es Gleichungen für bestimmte Formen gibt, um es einfacher zu machen). Sie müssen jedoch die Länge aller Seiten der Form kennen.[1]  2 Fügen Sie die Länge aller Seiten zusammen. Um den Umfang von nicht kreisförmigen Objekten zu finden, ermitteln Sie die Summe aller Seitenlängen, um den Abstand um die Form zu bestimmen.[2]
2 Fügen Sie die Länge aller Seiten zusammen. Um den Umfang von nicht kreisförmigen Objekten zu finden, ermitteln Sie die Summe aller Seitenlängen, um den Abstand um die Form zu bestimmen.[2]  3 Umgang mit Variablen. Sie können Perimeter immer noch finden, wenn Sie mit Variablen arbeiten. Angenommen, Sie haben ein Dreieck mit den Seitenlängen 14a, 11b und 7a:[3]
3 Umgang mit Variablen. Sie können Perimeter immer noch finden, wenn Sie mit Variablen arbeiten. Angenommen, Sie haben ein Dreieck mit den Seitenlängen 14a, 11b und 7a:[3]  4 Achten Sie auf Maßeinheiten. In einer realen Anwendung reicht es nicht aus, den Umfang eines Objekts zu finden, wenn Sie nicht wissen, mit welcher Maßeinheit Sie arbeiten (z. B. Fuß, Kilometer oder Meter). Wenn mit dem Fünfeck jede Seite in Zentimetern gemessen wurde, dann wissen Sie, dass P = 14 cm ist.
4 Achten Sie auf Maßeinheiten. In einer realen Anwendung reicht es nicht aus, den Umfang eines Objekts zu finden, wenn Sie nicht wissen, mit welcher Maßeinheit Sie arbeiten (z. B. Fuß, Kilometer oder Meter). Wenn mit dem Fünfeck jede Seite in Zentimetern gemessen wurde, dann wissen Sie, dass P = 14 cm ist. 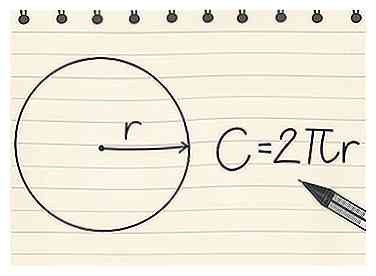 1 Finde den Umfang eines Kreises. Einige reguläre Formen haben Formeln, die es schneller machen, den Umfang der Figur zu finden. Aber es gibt andere Formen wie Kreise, die eine Formel benötigen, um den Umfang zu finden. Der Umfang eines Kreises wird Umfang genannt. Um den Umfang eines Kreises zu finden, verwenden Sie die Gleichung C (Umfang) = 2πr.[4]
1 Finde den Umfang eines Kreises. Einige reguläre Formen haben Formeln, die es schneller machen, den Umfang der Figur zu finden. Aber es gibt andere Formen wie Kreise, die eine Formel benötigen, um den Umfang zu finden. Der Umfang eines Kreises wird Umfang genannt. Um den Umfang eines Kreises zu finden, verwenden Sie die Gleichung C (Umfang) = 2πr.[4]  2 Finde den Umfang eines Dreiecks. Verwenden Sie die Gleichung P = a + b + c für ein Dreieck. Wenn beispielsweise ein Dreieck die Abmessungen a = 20 cm, b = 11 cm und c = 9 cm hat, dann ist P = 20 + 11 + 9 = 40 cm.
2 Finde den Umfang eines Dreiecks. Verwenden Sie die Gleichung P = a + b + c für ein Dreieck. Wenn beispielsweise ein Dreieck die Abmessungen a = 20 cm, b = 11 cm und c = 9 cm hat, dann ist P = 20 + 11 + 9 = 40 cm. 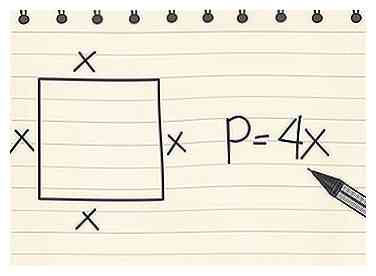 3 Finde den Umfang eines Quadrats. Da ein Quadrat vier Seiten gleicher Länge hat, können Sie die einfache Gleichung P = 4x verwenden, wobei x der Länge einer Seite entspricht.
3 Finde den Umfang eines Quadrats. Da ein Quadrat vier Seiten gleicher Länge hat, können Sie die einfache Gleichung P = 4x verwenden, wobei x der Länge einer Seite entspricht.  4 Finde den Umfang eines Rechtecks. Da die Längsseiten die gleichen sind und die Breitenseiten auf einem Rechteck gleich sind, können Sie die Gleichung P = 2l + 2w verwenden, wobei l die Länge einer Seite und w die Breite einer Seite ist. Für ein Rechteck mit l = 8cm und w = 5cm:
4 Finde den Umfang eines Rechtecks. Da die Längsseiten die gleichen sind und die Breitenseiten auf einem Rechteck gleich sind, können Sie die Gleichung P = 2l + 2w verwenden, wobei l die Länge einer Seite und w die Breite einer Seite ist. Für ein Rechteck mit l = 8cm und w = 5cm:  5 Finde den Umfang anderer Vierecke. Ein Viereck bezieht sich auf jede zweidimensionale Form mit vier geschlossenen, geraden Seiten. Dazu gehören Rechtecke, Quadrate, Trapeze, Parallelogramme, Drachen und Rhomben.[6] Je nach den Seiten gibt es drei Gleichungen für ein Viereck:
5 Finde den Umfang anderer Vierecke. Ein Viereck bezieht sich auf jede zweidimensionale Form mit vier geschlossenen, geraden Seiten. Dazu gehören Rechtecke, Quadrate, Trapeze, Parallelogramme, Drachen und Rhomben.[6] Je nach den Seiten gibt es drei Gleichungen für ein Viereck: