Dieses Tutorial enthält Schritt für Schritt Anweisungen zum Schreiben eines Skripts, das eine stückweise Funktion grafisch darstellt. Während die Programmierung für diejenigen, die neu darin sind, wie eine entmutigende Aufgabe erscheinen kann, werden diese Anweisungen sicherstellen, dass Sie keine Probleme haben werden, einen Code zu programmieren, der eine stückweise Funktion in MATLAB darstellt. Für dieses Tutorial nehmen wir die Gleichungen x ^ 2 - 3x + 12 (0 <= x <= 2), x ^ 3 + 5 (3 <= x <5), x ^ 2 - 22 (6 <= x <8), x ^ 2 + 12 (8
Schritte
- 1 Öffnen Sie MATLAB.
- 2
 Bewegen Sie die Maus ganz nach links in der Editorleiste und klicken Sie auf das Symbol mit dem neuen Skript.
Bewegen Sie die Maus ganz nach links in der Editorleiste und klicken Sie auf das Symbol mit dem neuen Skript. - Dies öffnet ein Fenster namens Skript direkt über Ihrem Befehlsmenü, das sich in der Mitte Ihres Bildschirms befindet.
- 3 Beginnen Sie Ihr Skript, indem Sie den Benutzer auffordern, einen numerischen Wert für das Zeichen x einzugeben (wir können diesem Wert ein beliebiges Zeichen zuweisen, aber wir verwenden x). Dieser Wert wird in die Funktionen eingehen, die grafisch dargestellt werden.
- 4 Geben Sie x = input () in Ihrem Skript als Ihre erste Zeile ein. Dies verwendet den Eingabebefehl von MATLAB, der es dem Benutzer erlaubt, nach dem Aufruf des Skripts eine beliebige Zahl im Befehlsmenü einzugeben (dies wird später in dieser Anleitung gezeigt).
- 5 Schreiben Sie einen numerischen Wert für x in die Klammern Ihres Eingabebefehls. Es sollte wie folgt aussehen: x = Eingabe ('Typ numerischer Wert für x:'). Wenn der Benutzer das Skript aufruft, wird dies im Befehlsmenü angezeigt, was den Benutzer auffordert, dem Zeichen x einen numerischen Wert zuzuweisen. Ihre erste Zeile ist nun vollständig.
- 6 Definieren Sie alle vier Gleichungen als anonyme Funktion für die Zeichen f1, f2, f3 und f4 in separaten Zeilen, beginnend mit "f1" als Zeile zwei und endend mit "f4" als Zeile fünf. Nur so können die Gleichungen innerhalb des Skripts liegen und ordnungsgemäß ausgeführt werden.
- Beim Schreiben Ihrer Funktion oder Gleichung ist es wichtig, dass Sie die arithmetischen Äquivalente in MATLAB kennen, damit MATLAB Ihren Code lesen kann. Addition ist +, Subtraktion ist -, Multiplikation ist *, Division ist / und Exponentiation ist ^.
- Es ist nicht nur wichtig, dass Sie die richtigen Symbole haben, sondern Sie müssen einen Punktoperator verwenden, wenn Sie einen Vektor von Werten innerhalb Ihrer Gleichung multiplizieren, dividieren oder potenzieren. Der Punktoperator ist ein Punkt Damit Sie ihn verwenden können, müssen Sie ihn vor Ihrer Multiplikation, Division und Potenzierung platzieren. Es sollte wie 2. * 2 + 5-2. ^ 2 aussehen
- 7 Wählen Sie das Zeichen aus, das Sie Ihrer Funktion oder Gleichung zuweisen möchten. Es sollte der Reihenfolge von character = function folgen. Die erste Funktion sollte als Beispiel aussehen wie "f1 = x. ^ 2 - 3. * x + 12"
-
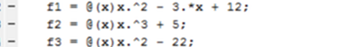 8 Fügen Sie ein "@ (Eingabezeichen)" vor Ihrer Funktion hinzu. Es sollte aussehen wie "character = @ (input character) function". Die erste Funktion sollte wie folgt aussehen: "f1 = @ (x) x. ^ 2 - 3. * x + 12".
8 Fügen Sie ein "@ (Eingabezeichen)" vor Ihrer Funktion hinzu. Es sollte aussehen wie "character = @ (input character) function". Die erste Funktion sollte wie folgt aussehen: "f1 = @ (x) x. ^ 2 - 3. * x + 12". - 9 Erstellen Sie in Zeile 6 in Ihrem Skript eine bedingte if-Anweisung. Auf diese Weise können Sie Bedingungen erstellen, die der Domäne jeder Ihrer stückweisen Funktionen entsprechen. Wenn die Bedingungen erfüllt sind, führt das Programm den Zeilencode aus, der unmittelbar auf Ihre Bedingung folgt. Wenn die Bedingungen nicht erfüllt sind, prüft MATLAB die Bedingungen in der nächsten Zeile mit bedingten Anweisungen und setzt fort, bis alle Bedingungen erfüllt sind oder keine Bedingungen mehr bestehen.
- 10 Folgen Sie Ihrer if-bedingten Anweisung in Zeile sechs, Sie müssen die Bedingungen mit den logischen Operatoren von MATLAB schreiben. Die logischen Operatoren dafür sind &,>, <,> =, <=. Um den Operator & zu überspringen, haben Sie größer als, kleiner als, größer als oder gleich und kleiner als oder gleich. Der Operator & ist ein Sonderfall, da er MATLAB mitteilt, dass alle bedingten Anweisungen in der Zeile für den manuell eingegebenen x-Wert wahr sein müssen, um den Code auszuführen, andernfalls geht MATLAB weiter, um den Wert in der nächsten Zeile mit Bedingung zu testen Aussagen.
- 11 Schreibe x> = 0 & x <2 nach der if-Anweisung, um Zeile sechs zu vervollständigen. Dies geschieht, weil die Funktion f1 = @ (x) x. ^ 2 - 3 ist. * X + 12 Domäne ist zwischen null und zwei, zwei ausgeschlossen, und der bedingte Zustand erfüllt die Domäne.
- 12In den Zeilen sieben und acht müssen Sie den Code schreiben, der ausgeführt werden soll, wenn die Bedingungen in Zeile sechs erfüllt sind.
- 13 Schreibe y = f1 (x) in Zeile sieben. Dies teilt dem Skript die Gleichung mit, die grafisch dargestellt werden soll, abhängig vom x-Wert, den der Benutzer manuell eingibt.
- 14
 Schreibe fplot (f1, [0,2]) in Zeile acht. Dies verwendet den fplot-Befehl in MATLAB, der es dem Benutzer ermöglicht, anonyme Funktionen zu zeichnen. f1 ist die grafisch dargestellte Funktion, während [0,2] die Domäne des Graphen ist.
Schreibe fplot (f1, [0,2]) in Zeile acht. Dies verwendet den fplot-Befehl in MATLAB, der es dem Benutzer ermöglicht, anonyme Funktionen zu zeichnen. f1 ist die grafisch dargestellte Funktion, während [0,2] die Domäne des Graphen ist. - 15 Verwenden Sie die bedingte Anweisung von elseif in Zeile 9. Dies ist im Wesentlichen das Gleiche wie die if-Anweisung, aber Sie verwenden elseif, damit MATLAB den Code vollständig durchläuft. Wenn Sie if anstelle von elseif verwenden, sieht MATLAB innerhalb eines Skripts zwei separate Codezweige, was sich nachteilig auswirkt, da wir sie als eine Einheit verwenden müssen.
- 16 Folgen Sie Ihrer bedingten elseif-Anweisung in Zeile 9. Schreiben Sie die Bedingungen ähnlich wie nach der if-Anweisung.
- 17 Schreibe x> = 3 & x <5 nach der elsif-Anweisung, um Zeile neun zu vervollständigen. Dies geschieht, weil die Funktion f2 = @ (x) x. ^ 3 + 5; Domäne ist zwischen drei bis fünf, fünf ausgeschlossen, und die bedingte Anweisung erfüllt die Domäne.
- 18Schreiben Sie den Code, der ausgeführt werden soll, wenn die Bedingungen in Zeile 9 in den Zeilen 10 und 11 erfüllt sind.
- 19 Schreibe y = f2 (x) in Zeile zehn. Dies teilt dem Skript die Gleichung mit, die grafisch dargestellt werden soll, abhängig vom x-Wert, den der Benutzer manuell eingibt.
- 20
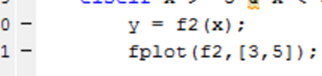 Schreibe fplot (f2, [3,5]) auf Zeile elf. Dies verwendet den fplot-Befehl in MATLAB.f2 ist die grafisch dargestellte Funktion, während [3,5] die Domäne des Graphen ist.
Schreibe fplot (f2, [3,5]) auf Zeile elf. Dies verwendet den fplot-Befehl in MATLAB.f2 ist die grafisch dargestellte Funktion, während [3,5] die Domäne des Graphen ist. - 21Verwenden Sie die bedingte Anweisung von elseif in Zeile 12.
- 22Folgen Sie Ihrer bedingten elseif-Anweisung in Zeile zwölf, Sie müssen die Bedingungen schreiben.
- 23 Schreibe x> = 6 & x <8 nach der elseif-Anweisung, um Zeile zwölf zu vervollständigen. Dies geschieht, weil die Funktion "f3 = @ (x) x. ^ 2 - 22" Domäne zwischen sechs und acht, acht ausgeschlossen ist, und die bedingte Anweisung erfüllt die Domäne.
- 24 Schreiben Sie den Code, der ausgeführt werden soll, wenn die Bedingungen in Zeile 12 erfüllt sind. Am 12. und 13.
- 25 Schreibe y = f3 (x) in Zeile dreizehn. Dies teilt dem Skript die Gleichung mit, die grafisch dargestellt werden soll, abhängig vom x-Wert, den der Benutzer manuell eingibt.
- 26
 Schreibe fplot (f3, [6,8]) in Zeile 14. Dies verwendet den fplot-Befehl in MATLAB. f3 ist die grafisch dargestellte Funktion, während [6,8] die Domäne des Graphen ist.
Schreibe fplot (f3, [6,8]) in Zeile 14. Dies verwendet den fplot-Befehl in MATLAB. f3 ist die grafisch dargestellte Funktion, während [6,8] die Domäne des Graphen ist. - 27Verwenden Sie die bedingte Anweisung von elseif in Zeile 15.
- 28Folgen Sie Ihrer eilif bedingten Anweisung in Zeile 15 Sie müssen die Bedingungen schreiben.
- 29 Schreibe x> 8 & x <= 10 nach der elseif-Anweisung, um Zeile 15 zu vervollständigen. Dies geschieht, weil die Funktion f4 = @ (x) x. ^ 2 + 12 Domäne zwischen acht und zehn, acht ausgeschlossen ist, und die bedingte Anweisung die Domäne erfüllt.
- 30 Schreiben Sie den Code, der ausgeführt werden soll, wenn die Bedingungen in Zeile 15 erfüllt sind. In den Zeilen 16 und 17.
- 31 Schreibe y = f4 (x) in Zeile 16. Dies teilt dem Skript die Gleichung mit, die grafisch dargestellt werden soll, abhängig vom x-Wert, den der Benutzer manuell eingibt.
- 32
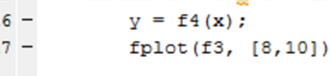 Schreibe fplot (f3, [8,10]) in Zeile 17. Dies verwendet den fplot-Befehl in MATLAB. f4 ist die grafisch dargestellte Funktion, während [8,10] die Domäne des Graphen ist.
Schreibe fplot (f3, [8,10]) in Zeile 17. Dies verwendet den fplot-Befehl in MATLAB. f4 ist die grafisch dargestellte Funktion, während [8,10] die Domäne des Graphen ist. - 33 Verwenden Sie die Else-Bedingungsanweisung. Dies entspricht im Wesentlichen den bedingten Anweisungen für if und elseif. Dies ist jedoch die letzte bedingte Anweisung, die MATLAB nach dem Testen aller anderen Anweisungen liest. Im Wesentlichen sind die Codes, die dieser Anweisung folgen, die letzten, die ausgeführt werden.
- 34Weisen Sie das Skript an, außerhalb des Bereichs anzuzeigen, indem Sie in Zeile 19 den Befehl display in MATLAB verwenden.
- 35Schreibe disp (außerhalb des Bereichs).
- 36
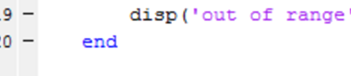 In Zeile 20 beenden Sie das Skript, indem Sie das Ende schreiben.
In Zeile 20 beenden Sie das Skript, indem Sie das Ende schreiben. - 37 Klicken Sie mit der rechten Maustaste auf den Speicherbereich mit einer Diskette als Symbol. Es befindet sich auf der Registerkarte "Editoren" und befindet sich einen Platz vom Symbol ganz links entfernt, das als neu bezeichnet wird und ein Kreuz für ein Symbol aufweist.
- Es sollte eine Dropdown-Box angezeigt werden. Wenn dies nicht der Fall ist, können Sie die Tastenkombination "Strg + S" verwenden. Klicken Sie auf Speichern unter.
- 38 Geben Sie den Namen, unter dem Sie Ihre Skriptdatei gespeichert haben, in das Befehlsfenster ein, um Ihr Skript aufzurufen (um ein Skript aufzurufen, müssen Sie den Skriptcode verwenden oder initiieren).). Nachdem Sie Ihr Skript aufgerufen haben, sollten Sie aufgefordert werden, im Befehlsfenster einen x-Wert einzugeben, der den numerischen Wert für x angibt.
-
 39 Geben Sie einen beliebigen Wert ein, der x sein soll. Jede Zahl zwischen null und zehn gibt Ihnen eine Grafik mit einer der Funktionen, außer zwei, fünf und acht. Zwei, fünf, acht und jede Zahl außerhalb von Null bis Zehn werden Ihnen außerhalb des Bereichs im Befehlsfenster sagen. Sie haben jetzt einen Arbeitscode für ein stückweises Diagramm. Oben ist ein Beispiel dafür, wie Sie Ihr Skript aufrufen können. Der verwendete Name ist Callscript und der numerische Wert für x ist drei.
39 Geben Sie einen beliebigen Wert ein, der x sein soll. Jede Zahl zwischen null und zehn gibt Ihnen eine Grafik mit einer der Funktionen, außer zwei, fünf und acht. Zwei, fünf, acht und jede Zahl außerhalb von Null bis Zehn werden Ihnen außerhalb des Bereichs im Befehlsfenster sagen. Sie haben jetzt einen Arbeitscode für ein stückweises Diagramm. Oben ist ein Beispiel dafür, wie Sie Ihr Skript aufrufen können. Der verwendete Name ist Callscript und der numerische Wert für x ist drei.
 Minotauromaquia
Minotauromaquia
 Bewegen Sie die Maus ganz nach links in der Editorleiste und klicken Sie auf das Symbol mit dem neuen Skript.
Bewegen Sie die Maus ganz nach links in der Editorleiste und klicken Sie auf das Symbol mit dem neuen Skript. 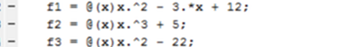 8 Fügen Sie ein "@ (Eingabezeichen)" vor Ihrer Funktion hinzu. Es sollte aussehen wie "character = @ (input character) function". Die erste Funktion sollte wie folgt aussehen: "f1 = @ (x) x. ^ 2 - 3. * x + 12".
8 Fügen Sie ein "@ (Eingabezeichen)" vor Ihrer Funktion hinzu. Es sollte aussehen wie "character = @ (input character) function". Die erste Funktion sollte wie folgt aussehen: "f1 = @ (x) x. ^ 2 - 3. * x + 12".  Schreibe fplot (f1, [0,2]) in Zeile acht. Dies verwendet den fplot-Befehl in MATLAB, der es dem Benutzer ermöglicht, anonyme Funktionen zu zeichnen. f1 ist die grafisch dargestellte Funktion, während [0,2] die Domäne des Graphen ist.
Schreibe fplot (f1, [0,2]) in Zeile acht. Dies verwendet den fplot-Befehl in MATLAB, der es dem Benutzer ermöglicht, anonyme Funktionen zu zeichnen. f1 ist die grafisch dargestellte Funktion, während [0,2] die Domäne des Graphen ist. 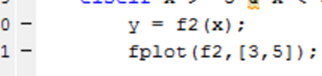 Schreibe fplot (f2, [3,5]) auf Zeile elf. Dies verwendet den fplot-Befehl in MATLAB.f2 ist die grafisch dargestellte Funktion, während [3,5] die Domäne des Graphen ist.
Schreibe fplot (f2, [3,5]) auf Zeile elf. Dies verwendet den fplot-Befehl in MATLAB.f2 ist die grafisch dargestellte Funktion, während [3,5] die Domäne des Graphen ist.  Schreibe fplot (f3, [6,8]) in Zeile 14. Dies verwendet den fplot-Befehl in MATLAB. f3 ist die grafisch dargestellte Funktion, während [6,8] die Domäne des Graphen ist.
Schreibe fplot (f3, [6,8]) in Zeile 14. Dies verwendet den fplot-Befehl in MATLAB. f3 ist die grafisch dargestellte Funktion, während [6,8] die Domäne des Graphen ist. 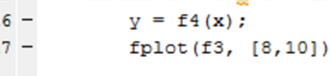 Schreibe fplot (f3, [8,10]) in Zeile 17. Dies verwendet den fplot-Befehl in MATLAB. f4 ist die grafisch dargestellte Funktion, während [8,10] die Domäne des Graphen ist.
Schreibe fplot (f3, [8,10]) in Zeile 17. Dies verwendet den fplot-Befehl in MATLAB. f4 ist die grafisch dargestellte Funktion, während [8,10] die Domäne des Graphen ist.  In Zeile 20 beenden Sie das Skript, indem Sie das Ende schreiben.
In Zeile 20 beenden Sie das Skript, indem Sie das Ende schreiben.  39 Geben Sie einen beliebigen Wert ein, der x sein soll. Jede Zahl zwischen null und zehn gibt Ihnen eine Grafik mit einer der Funktionen, außer zwei, fünf und acht. Zwei, fünf, acht und jede Zahl außerhalb von Null bis Zehn werden Ihnen außerhalb des Bereichs im Befehlsfenster sagen. Sie haben jetzt einen Arbeitscode für ein stückweises Diagramm. Oben ist ein Beispiel dafür, wie Sie Ihr Skript aufrufen können. Der verwendete Name ist Callscript und der numerische Wert für x ist drei.
39 Geben Sie einen beliebigen Wert ein, der x sein soll. Jede Zahl zwischen null und zehn gibt Ihnen eine Grafik mit einer der Funktionen, außer zwei, fünf und acht. Zwei, fünf, acht und jede Zahl außerhalb von Null bis Zehn werden Ihnen außerhalb des Bereichs im Befehlsfenster sagen. Sie haben jetzt einen Arbeitscode für ein stückweises Diagramm. Oben ist ein Beispiel dafür, wie Sie Ihr Skript aufrufen können. Der verwendete Name ist Callscript und der numerische Wert für x ist drei.