Einfach Ordnung Magische Quadrate sind die, die durch 2 teilbar sind, aber nicht durch 4. Das früheste Quadrat wäre 6x6 Ordnung Quadrat, dann haben wir 10x10, 14x14, 18x18 etc.
Schritte
-
 1 SINGLY AUCH ORDEN - 6X6 SQUARE.
1 SINGLY AUCH ORDEN - 6X6 SQUARE. -
 2 Jetzt sehen wir uns 6x6 Quadrate an. 6x6 Quadrat wird Zahlen von 1 bis 36 haben, während 4x4 Quadrat Zahlen von 1 bis 16 hatte. 36-16 = 20/2 = 10. Lassen Sie uns 10 zu allen Zahlen von jedem 4x4 Quadrat hinzufügen, um ein 4x4 Quadrat mit einer Gesamtheit von 74 zu erhalten. Dieses 4x4 Quadrat werden wir als 2x2 Quadrate in den 4 Ecken auf dem linken 6x6 Quadrat setzen. Wir haben jetzt Zahlen von 1 bis 10 und 27 bis 36, um die leeren Plätze zu füllen.
2 Jetzt sehen wir uns 6x6 Quadrate an. 6x6 Quadrat wird Zahlen von 1 bis 36 haben, während 4x4 Quadrat Zahlen von 1 bis 16 hatte. 36-16 = 20/2 = 10. Lassen Sie uns 10 zu allen Zahlen von jedem 4x4 Quadrat hinzufügen, um ein 4x4 Quadrat mit einer Gesamtheit von 74 zu erhalten. Dieses 4x4 Quadrat werden wir als 2x2 Quadrate in den 4 Ecken auf dem linken 6x6 Quadrat setzen. Wir haben jetzt Zahlen von 1 bis 10 und 27 bis 36, um die leeren Plätze zu füllen. - 11 16 xx xx 21 26 'xx' steht für Orte, die noch gefüllt werden müssen.
- 25 22 xx xx 15 12
- xx xx xx xx xx xx
- xx xx xx xx xx xx
- 18 13 xx xx 24 19
- 20 23 xx xx 17 17
-
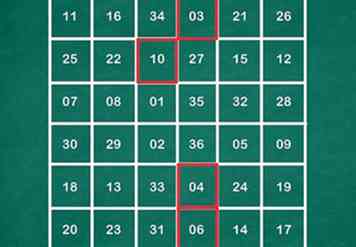
 3 Wir werden nun zuerst die Diagonalen vervollständigen, indem wir 1 und 36 in eins und 2 und 35 in das andere einfügen. Der Rest der Zahlen ist so gefüllt, dass wir insgesamt 37 in den restlichen 2 Stellen in Zeilen und Spalten mit insgesamt 111 in jeder der dritten und vierten Spalten und Zeilen haben.
3 Wir werden nun zuerst die Diagonalen vervollständigen, indem wir 1 und 36 in eins und 2 und 35 in das andere einfügen. Der Rest der Zahlen ist so gefüllt, dass wir insgesamt 37 in den restlichen 2 Stellen in Zeilen und Spalten mit insgesamt 111 in jeder der dritten und vierten Spalten und Zeilen haben. -
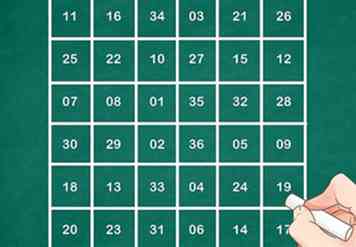 4 Das fertige 6x6 Quadrat wäre wie folgt:
4 Das fertige 6x6 Quadrat wäre wie folgt: - 11 16 34 03 21 26
- 25 22 10 27 15 12
- 07 08 01 35 32 28
- 30 29 02 36 05 09
- 18 13 33 04 24 19
- 20 23 31 06 14 17
-
 5
5 -
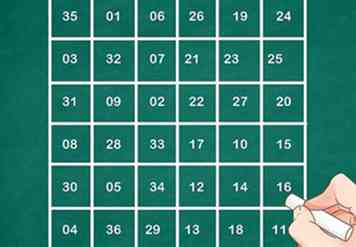 6 Wir haben 880 Quadrate zur Auswahl, und für die Platzierung von 3,4,6 und 10 haben wir 24 Auswahlmöglichkeiten. Dies liegt daran, dass wir 4 Möglichkeiten haben, die erste Nummer zu platzieren, 3 Optionen für die nächste Nummer und 2 Optionen für die nächste Nummer. Ähnlich haben wir für die Platzierung von 5, 7, 8 und 9 24 Möglichkeiten, so dass wir leicht 880x24x24 alle verschiedenen Quadrate erhalten. Weiter für die Diagonalen haben wir die Möglichkeit, die Nummern zu wählen. Anstelle von 1 und 2 hätten wir 9 und 10 wählen können. Eine verfügbare Kombination wäre 1,9,10 für eine Spalte und 5,7,8 für die andere und 3,4,10 für eine Zeile und 2,6 , 9 für die andere Reihe. Erarbeiten Sie andere Kombinationen und jeder wird 880x24x24 neue 6x6 Quadrate ergeben?
6 Wir haben 880 Quadrate zur Auswahl, und für die Platzierung von 3,4,6 und 10 haben wir 24 Auswahlmöglichkeiten. Dies liegt daran, dass wir 4 Möglichkeiten haben, die erste Nummer zu platzieren, 3 Optionen für die nächste Nummer und 2 Optionen für die nächste Nummer. Ähnlich haben wir für die Platzierung von 5, 7, 8 und 9 24 Möglichkeiten, so dass wir leicht 880x24x24 alle verschiedenen Quadrate erhalten. Weiter für die Diagonalen haben wir die Möglichkeit, die Nummern zu wählen. Anstelle von 1 und 2 hätten wir 9 und 10 wählen können. Eine verfügbare Kombination wäre 1,9,10 für eine Spalte und 5,7,8 für die andere und 3,4,10 für eine Zeile und 2,6 , 9 für die andere Reihe. Erarbeiten Sie andere Kombinationen und jeder wird 880x24x24 neue 6x6 Quadrate ergeben? -
 7
7 -
 8 Natürlich gibt es andere Methoden, die 6x6-Quadrate auszuarbeiten, um uns viel mehr 6x6-Quadrate zu geben. Wir hätten das 4x4-Quadrat mit insgesamt 74 als Mittelfeld platzieren können und die Zahlen von 1 bis 10 und 27 bis 36 in den leeren Plätzen auf den Plätzen der 1. 2., 5. und 6. Spalte und 1. 2., 5. gefüllt und 6. Reihen. Es gibt auch andere Methoden, versuchen Sie, das 4x4-Quadrat mit insgesamt 74 in den ersten bis vierten Reihen und Spalten zu setzen und die 5. und 6. Spalte und Reihen mit den verfügbaren Zahlen aufzufüllen? Versuchen Sie es auch anders.
8 Natürlich gibt es andere Methoden, die 6x6-Quadrate auszuarbeiten, um uns viel mehr 6x6-Quadrate zu geben. Wir hätten das 4x4-Quadrat mit insgesamt 74 als Mittelfeld platzieren können und die Zahlen von 1 bis 10 und 27 bis 36 in den leeren Plätzen auf den Plätzen der 1. 2., 5. und 6. Spalte und 1. 2., 5. gefüllt und 6. Reihen. Es gibt auch andere Methoden, versuchen Sie, das 4x4-Quadrat mit insgesamt 74 in den ersten bis vierten Reihen und Spalten zu setzen und die 5. und 6. Spalte und Reihen mit den verfügbaren Zahlen aufzufüllen? Versuchen Sie es auch anders. -
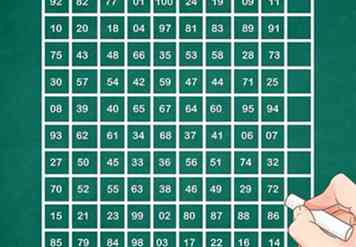
 9 Ein 10x10-Bestellplatz wird Zahlen von 1 bis 100 mit insgesamt 505 haben. 6x6 Ordnung Quadrat hatte Zahlen von 1 bis 36. 100-36 = 64, 64/2 ist 32. Also fügen wir 32 zu allen Zahlen im Quadrat der Ordnung 6x6 hinzu, um eins mit einer Summe von 303 zu erhalten. Dieses wird in der Mitte gelegt und leere Felder werden zuerst mit drei 4x4 Quadraten gefüllt, ein Quadrat hat die Nummern 9 bis 16 und 85 bis 92, 2. von 17 bis 24 und 77 bis 84 und das 3. von 25 bis 32 und 69 bis 76. Jetzt wird es sein 16 Felder sind zu füllen, 8 in den Spalten 5, 6, und Zeilen 1, 2, 9 und 10, und 8 in den Zeilen 5, 6 und den Spalten 1, 2, 9 und 10. Wir müssen sicherstellen, dass die Menge der Zahlen sind so, dass in dem ersten Fall die Zeilen 101 und in dem zweiten Fall die Spalten 101 insgesamt sind, zusammen mit dem Sicherstellen, dass die Spaltensumme 202 in der ersten Zeile ist und die Zeilensumme 202 in dem zweiten Fall ist. Wenn wir die kleineren Zahlen mit den gleichen Summen in den Spalten und Zeilen auswählen, erhalten wir die richtigen Summen. Aus diesem Grund wurden 1 & 4, 2 & 3, 5 & 8 und 6 & 7 ausgewählt.
9 Ein 10x10-Bestellplatz wird Zahlen von 1 bis 100 mit insgesamt 505 haben. 6x6 Ordnung Quadrat hatte Zahlen von 1 bis 36. 100-36 = 64, 64/2 ist 32. Also fügen wir 32 zu allen Zahlen im Quadrat der Ordnung 6x6 hinzu, um eins mit einer Summe von 303 zu erhalten. Dieses wird in der Mitte gelegt und leere Felder werden zuerst mit drei 4x4 Quadraten gefüllt, ein Quadrat hat die Nummern 9 bis 16 und 85 bis 92, 2. von 17 bis 24 und 77 bis 84 und das 3. von 25 bis 32 und 69 bis 76. Jetzt wird es sein 16 Felder sind zu füllen, 8 in den Spalten 5, 6, und Zeilen 1, 2, 9 und 10, und 8 in den Zeilen 5, 6 und den Spalten 1, 2, 9 und 10. Wir müssen sicherstellen, dass die Menge der Zahlen sind so, dass in dem ersten Fall die Zeilen 101 und in dem zweiten Fall die Spalten 101 insgesamt sind, zusammen mit dem Sicherstellen, dass die Spaltensumme 202 in der ersten Zeile ist und die Zeilensumme 202 in dem zweiten Fall ist. Wenn wir die kleineren Zahlen mit den gleichen Summen in den Spalten und Zeilen auswählen, erhalten wir die richtigen Summen. Aus diesem Grund wurden 1 & 4, 2 & 3, 5 & 8 und 6 & 7 ausgewählt. - 92 82 77 01 100 24 19 09 11
- 10 20 18 04 097 81 83 89 91
- 75 43 48 66 035 53 58 28 73
- 30 57 54 42 059 47 44 71 25
- 08 39 40 65 067 64 60 95 94
- 93 62 61 34 068 37 41 06 07
- 27 50 45 33 036 56 51 74 32
- 70 52 55 63 038 46 49 29 72
- 15 21 23 99 002 80 78 88 86
- 85 79 84 98 003 17 22 16 14
- 10 Wir haben die Wahl, Zahlen von 1 bis 8 zu platzieren, wie es uns gefällt. So kann die Anzahl der 6x6 Quadrate mit 8x6x4x2 multipliziert werden, um die Anzahl der Quadrate für das 10x10 Quadrat zu erhalten. Natürlich gibt es andere Möglichkeiten, die 10x10 Quadrate zu konstruieren, so dass die Anzahl der möglichen Quadrate nur vorstellbar ist.
- 11 Für das Quadrat 14x14 können wir dasselbe Verfahren befolgen, indem wir mit einem Quadrat 10x10 beginnen, in dem 196-100 = 96, 96/2 = 48, zu allen Zahlen addiert wurden, um insgesamt 985 zu ergeben. Benötigt wird insgesamt 14 (1 + 196) / 2 = 1379. Wir müssen sieben 4x4 Quadrate mit insgesamt 394 einfügen und die restlichen 16 Felder mit Zahlen von 1 bis 8 und 189 bis 196 füllen. Wir können die Zahlen platzieren von 1 bis 8 wie auf dem 10x10 Quadrat. Ähnlich können wir von 14x14 Quadrat zu dem 18x18 Quadrat und so weiter gehen.
 Minotauromaquia
Minotauromaquia
 1 SINGLY AUCH ORDEN - 6X6 SQUARE.
1 SINGLY AUCH ORDEN - 6X6 SQUARE.  2 Jetzt sehen wir uns 6x6 Quadrate an. 6x6 Quadrat wird Zahlen von 1 bis 36 haben, während 4x4 Quadrat Zahlen von 1 bis 16 hatte. 36-16 = 20/2 = 10. Lassen Sie uns 10 zu allen Zahlen von jedem 4x4 Quadrat hinzufügen, um ein 4x4 Quadrat mit einer Gesamtheit von 74 zu erhalten. Dieses 4x4 Quadrat werden wir als 2x2 Quadrate in den 4 Ecken auf dem linken 6x6 Quadrat setzen. Wir haben jetzt Zahlen von 1 bis 10 und 27 bis 36, um die leeren Plätze zu füllen.
2 Jetzt sehen wir uns 6x6 Quadrate an. 6x6 Quadrat wird Zahlen von 1 bis 36 haben, während 4x4 Quadrat Zahlen von 1 bis 16 hatte. 36-16 = 20/2 = 10. Lassen Sie uns 10 zu allen Zahlen von jedem 4x4 Quadrat hinzufügen, um ein 4x4 Quadrat mit einer Gesamtheit von 74 zu erhalten. Dieses 4x4 Quadrat werden wir als 2x2 Quadrate in den 4 Ecken auf dem linken 6x6 Quadrat setzen. Wir haben jetzt Zahlen von 1 bis 10 und 27 bis 36, um die leeren Plätze zu füllen.  3 Wir werden nun zuerst die Diagonalen vervollständigen, indem wir 1 und 36 in eins und 2 und 35 in das andere einfügen. Der Rest der Zahlen ist so gefüllt, dass wir insgesamt 37 in den restlichen 2 Stellen in Zeilen und Spalten mit insgesamt 111 in jeder der dritten und vierten Spalten und Zeilen haben.
3 Wir werden nun zuerst die Diagonalen vervollständigen, indem wir 1 und 36 in eins und 2 und 35 in das andere einfügen. Der Rest der Zahlen ist so gefüllt, dass wir insgesamt 37 in den restlichen 2 Stellen in Zeilen und Spalten mit insgesamt 111 in jeder der dritten und vierten Spalten und Zeilen haben.  4 Das fertige 6x6 Quadrat wäre wie folgt:
4 Das fertige 6x6 Quadrat wäre wie folgt:  5
5  6 Wir haben 880 Quadrate zur Auswahl, und für die Platzierung von 3,4,6 und 10 haben wir 24 Auswahlmöglichkeiten. Dies liegt daran, dass wir 4 Möglichkeiten haben, die erste Nummer zu platzieren, 3 Optionen für die nächste Nummer und 2 Optionen für die nächste Nummer. Ähnlich haben wir für die Platzierung von 5, 7, 8 und 9 24 Möglichkeiten, so dass wir leicht 880x24x24 alle verschiedenen Quadrate erhalten. Weiter für die Diagonalen haben wir die Möglichkeit, die Nummern zu wählen. Anstelle von 1 und 2 hätten wir 9 und 10 wählen können. Eine verfügbare Kombination wäre 1,9,10 für eine Spalte und 5,7,8 für die andere und 3,4,10 für eine Zeile und 2,6 , 9 für die andere Reihe. Erarbeiten Sie andere Kombinationen und jeder wird 880x24x24 neue 6x6 Quadrate ergeben?
6 Wir haben 880 Quadrate zur Auswahl, und für die Platzierung von 3,4,6 und 10 haben wir 24 Auswahlmöglichkeiten. Dies liegt daran, dass wir 4 Möglichkeiten haben, die erste Nummer zu platzieren, 3 Optionen für die nächste Nummer und 2 Optionen für die nächste Nummer. Ähnlich haben wir für die Platzierung von 5, 7, 8 und 9 24 Möglichkeiten, so dass wir leicht 880x24x24 alle verschiedenen Quadrate erhalten. Weiter für die Diagonalen haben wir die Möglichkeit, die Nummern zu wählen. Anstelle von 1 und 2 hätten wir 9 und 10 wählen können. Eine verfügbare Kombination wäre 1,9,10 für eine Spalte und 5,7,8 für die andere und 3,4,10 für eine Zeile und 2,6 , 9 für die andere Reihe. Erarbeiten Sie andere Kombinationen und jeder wird 880x24x24 neue 6x6 Quadrate ergeben?  7
7  8 Natürlich gibt es andere Methoden, die 6x6-Quadrate auszuarbeiten, um uns viel mehr 6x6-Quadrate zu geben. Wir hätten das 4x4-Quadrat mit insgesamt 74 als Mittelfeld platzieren können und die Zahlen von 1 bis 10 und 27 bis 36 in den leeren Plätzen auf den Plätzen der 1. 2., 5. und 6. Spalte und 1. 2., 5. gefüllt und 6. Reihen. Es gibt auch andere Methoden, versuchen Sie, das 4x4-Quadrat mit insgesamt 74 in den ersten bis vierten Reihen und Spalten zu setzen und die 5. und 6. Spalte und Reihen mit den verfügbaren Zahlen aufzufüllen? Versuchen Sie es auch anders.
8 Natürlich gibt es andere Methoden, die 6x6-Quadrate auszuarbeiten, um uns viel mehr 6x6-Quadrate zu geben. Wir hätten das 4x4-Quadrat mit insgesamt 74 als Mittelfeld platzieren können und die Zahlen von 1 bis 10 und 27 bis 36 in den leeren Plätzen auf den Plätzen der 1. 2., 5. und 6. Spalte und 1. 2., 5. gefüllt und 6. Reihen. Es gibt auch andere Methoden, versuchen Sie, das 4x4-Quadrat mit insgesamt 74 in den ersten bis vierten Reihen und Spalten zu setzen und die 5. und 6. Spalte und Reihen mit den verfügbaren Zahlen aufzufüllen? Versuchen Sie es auch anders.  9 Ein 10x10-Bestellplatz wird Zahlen von 1 bis 100 mit insgesamt 505 haben. 6x6 Ordnung Quadrat hatte Zahlen von 1 bis 36. 100-36 = 64, 64/2 ist 32. Also fügen wir 32 zu allen Zahlen im Quadrat der Ordnung 6x6 hinzu, um eins mit einer Summe von 303 zu erhalten. Dieses wird in der Mitte gelegt und leere Felder werden zuerst mit drei 4x4 Quadraten gefüllt, ein Quadrat hat die Nummern 9 bis 16 und 85 bis 92, 2. von 17 bis 24 und 77 bis 84 und das 3. von 25 bis 32 und 69 bis 76. Jetzt wird es sein 16 Felder sind zu füllen, 8 in den Spalten 5, 6, und Zeilen 1, 2, 9 und 10, und 8 in den Zeilen 5, 6 und den Spalten 1, 2, 9 und 10. Wir müssen sicherstellen, dass die Menge der Zahlen sind so, dass in dem ersten Fall die Zeilen 101 und in dem zweiten Fall die Spalten 101 insgesamt sind, zusammen mit dem Sicherstellen, dass die Spaltensumme 202 in der ersten Zeile ist und die Zeilensumme 202 in dem zweiten Fall ist. Wenn wir die kleineren Zahlen mit den gleichen Summen in den Spalten und Zeilen auswählen, erhalten wir die richtigen Summen. Aus diesem Grund wurden 1 & 4, 2 & 3, 5 & 8 und 6 & 7 ausgewählt.
9 Ein 10x10-Bestellplatz wird Zahlen von 1 bis 100 mit insgesamt 505 haben. 6x6 Ordnung Quadrat hatte Zahlen von 1 bis 36. 100-36 = 64, 64/2 ist 32. Also fügen wir 32 zu allen Zahlen im Quadrat der Ordnung 6x6 hinzu, um eins mit einer Summe von 303 zu erhalten. Dieses wird in der Mitte gelegt und leere Felder werden zuerst mit drei 4x4 Quadraten gefüllt, ein Quadrat hat die Nummern 9 bis 16 und 85 bis 92, 2. von 17 bis 24 und 77 bis 84 und das 3. von 25 bis 32 und 69 bis 76. Jetzt wird es sein 16 Felder sind zu füllen, 8 in den Spalten 5, 6, und Zeilen 1, 2, 9 und 10, und 8 in den Zeilen 5, 6 und den Spalten 1, 2, 9 und 10. Wir müssen sicherstellen, dass die Menge der Zahlen sind so, dass in dem ersten Fall die Zeilen 101 und in dem zweiten Fall die Spalten 101 insgesamt sind, zusammen mit dem Sicherstellen, dass die Spaltensumme 202 in der ersten Zeile ist und die Zeilensumme 202 in dem zweiten Fall ist. Wenn wir die kleineren Zahlen mit den gleichen Summen in den Spalten und Zeilen auswählen, erhalten wir die richtigen Summen. Aus diesem Grund wurden 1 & 4, 2 & 3, 5 & 8 und 6 & 7 ausgewählt.