Primzahlen, die einst als mathematische Neuheit galten, sind mit dem Aufkommen des Internets und moderner Verschlüsselungstechniken in die Blütezeit eingetreten. Bei der Entscheidung, ob eine 1024-stellige Primzahl rechnerisch schwierig sein kann, können Sie selbst mit etwas Übung die Primzahl einer 3-stelligen Zahl in Ihrem Kopf bestimmen!
Und wie bei allen mentalen Mathetricks, wie Jonglieren und Einradfahren, ist es die Kunst des Angeberns. Wenn Sie diese Erklärung lesen und ihre Prinzipien anwenden, wird Ihre Geist-Auge-Koordination sicherlich einen großen Schritt nach vorne machen, aber vor allem werden Sie Ihre Freunde mit Ihrer Fähigkeit zur Berechnung verblüffen können!
Schritte
-
 1 Besorge Bleistift und Papier. Wie bei jedem mathematischen Prinzip werden Sie sich besser daran erinnern, wenn Sie gleichzeitig auf dem Papier üben.
1 Besorge Bleistift und Papier. Wie bei jedem mathematischen Prinzip werden Sie sich besser daran erinnern, wenn Sie gleichzeitig auf dem Papier üben. -
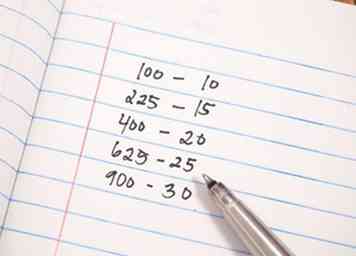 2 Schätzen Sie die Quadratwurzel der Zahl. Dies wird Ihre Prüfung beschleunigen, da nur versucht werden muss, die mögliche Primzahl durch die Primzahlen zu dividieren, die kleiner sind als die Quadratwurzel dieser Zahl. Ein kurzer Hinweis könnte helfen: Die Quadratwurzel von 100 ist 10, von 225 ist 15, von 400 ist 20, von 625 ist 25 und von 900 ist 30.
2 Schätzen Sie die Quadratwurzel der Zahl. Dies wird Ihre Prüfung beschleunigen, da nur versucht werden muss, die mögliche Primzahl durch die Primzahlen zu dividieren, die kleiner sind als die Quadratwurzel dieser Zahl. Ein kurzer Hinweis könnte helfen: Die Quadratwurzel von 100 ist 10, von 225 ist 15, von 400 ist 20, von 625 ist 25 und von 900 ist 30. -
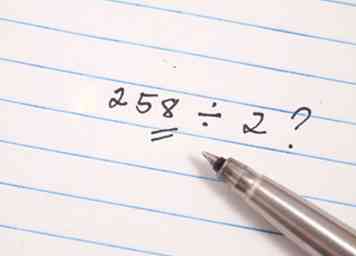 3 Erfahren Sie, wie Sie schnell erkennen können, ob eine Zahl durch 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 oder 31 teilbar ist. Da die Quadratwurzel von 1000 ungefähr 33 ist, müssen Sie nie eine Zahl höher als 31 testen. Indem Sie die Anzahl der Tests auf 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 verringern, und 31 hast du schon die halbe Miete gewonnen.
3 Erfahren Sie, wie Sie schnell erkennen können, ob eine Zahl durch 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 oder 31 teilbar ist. Da die Quadratwurzel von 1000 ungefähr 33 ist, müssen Sie nie eine Zahl höher als 31 testen. Indem Sie die Anzahl der Tests auf 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 verringern, und 31 hast du schon die halbe Miete gewonnen. - Hier sind die Teilbarkeitsregeln für diese Primzahlen:
- Teilbar durch 2 - Wenn die Nummer in 2, 4, 6 oder 8 endet
- Teilbar durch 3 - Wenn die addierten Ziffern durch 3 teilbar sind
- Teilbar durch 5 - Wenn die Nummer in 0 oder 5 endet
- Teilbar durch 7 - Nimm die letzte Ziffer und multipliziere sie mit zwei. Subtrahiere diese Zahl von den restlichen Ziffern. Die ursprüngliche Zahl ist durch 7 teilbar, wenn die neue Zahl durch 7 teilbar ist.
- Teilbar bis 11 - Nimm die letzte Ziffer. Subtrahiere diese Zahl von den restlichen Ziffern. Die ursprüngliche Zahl ist durch 11 teilbar, wenn diese neue Zahl durch 11 teilbar ist.
- Teilbar bis 13 - Nimm die letzte Ziffer und multipliziere sie mit vier. Fügen Sie diese Nummer zu den restlichen Ziffern hinzu. Die ursprüngliche Zahl ist durch 13 teilbar, wenn die neue Zahl durch 13 teilbar ist.
- Teilbar bis 17 - Nimm die letzte Ziffer und multipliziere sie mit fünf. Subtrahiere diese Zahl von den restlichen Ziffern. Die ursprüngliche Zahl ist durch 17 teilbar, wenn die neue Zahl durch 17 teilbar ist. (Dies klingt härter als es aussieht. Ein Beispiel unten veranschaulicht dies.)
- Teilbar bis 19 - Nimm die letzte Ziffer und multipliziere sie mit zwei. Fügen Sie diese Nummer zu den restlichen Ziffern hinzu. Die ursprüngliche Zahl ist durch 19 teilbar, wenn die neue Zahl durch 19 teilbar ist.
- Teilbar bis 23 - Nimm die letzte Ziffer und multipliziere sie mit sieben. Fügen Sie diese Nummer zu den restlichen Ziffern hinzu. Die ursprüngliche Zahl ist durch 23 teilbar, wenn die neue Zahl durch 23 teilbar ist.
- Teilbar bis 29 - Nimm die letzte Ziffer und multipliziere sie mit drei. Fügen Sie diese Nummer zu den restlichen Ziffern hinzu. Die ursprüngliche Zahl ist durch 29 teilbar, wenn die neue Zahl durch 29 teilbar ist.
- Teilbar bis 31 - Nimm die letzte Ziffer und multipliziere sie mit drei. Subtrahiere diese Zahl von den restlichen Ziffern. Die ursprüngliche Zahl ist durch 31 teilbar, wenn die neue Zahl durch 31 teilbar ist.
- Hier sind die Teilbarkeitsregeln für diese Primzahlen:
-
 4 Versuchen Sie, die mögliche Primzahl durch Primzahlen zu dividieren, die kleiner als die Quadratwurzel dieser Zahl sind.
4 Versuchen Sie, die mögliche Primzahl durch Primzahlen zu dividieren, die kleiner als die Quadratwurzel dieser Zahl sind. -
 5 Mit einem selbstsicheren Grinsen proklamieren, ob es Prime ist und was es teilbar ist!
5 Mit einem selbstsicheren Grinsen proklamieren, ob es Prime ist und was es teilbar ist! - Beispiel Lass uns 781 machen.
- Bleistift und Papier. Prüfen.
- Schätzen Sie die Quadratwurzel. 787 liegt zwischen 625 und 900, also weiß ich aus der obigen Tabelle, dass die Quadratwurzel von 787 zwischen 25 und 30 liegt, wahrscheinlich etwa 27. Also müssen die Primzahlen, auf die ich testen muss, 2, 3, 5, 7 sein. 11, 13, 17, 19 und 23. Die nächste Primzahl ist 29, und meine mentale Mathematik sagt mir, dass die Quadratwurzel von 787 wahrscheinlich nicht 29 ist, da sie nicht sehr nahe bei 900 liegt.
- Prüfen Sie die Teilbarkeit nach 2, 3, 5, 7, 11, 13, 17, 19 und 23.
- Um zwei: 781 endet nicht in 2, 4, 6 oder 8. So weit so gut.
- Um drei: Füge die Ziffern hinzu; 7 + 8 + 1 = 16. 16 ist nicht durch 3 teilbar, also auch nicht 781.
- Um fünf: 781 endet nicht in 0 oder 5. Noch Prime.
- Um sieben: Multiplizieren Sie die letzte Ziffer mit zwei; 1 * 2 = 2. Subtrahiere es von den restlichen Ziffern; 78 - 2 = 76. 76 ist nicht durch 7 teilbar (erinnere dich, dass 70 ist und 77 ist), also auch nicht 781.
- Bis elf: Subtrahiere die letzte Ziffer von den restlichen Ziffern; 78 - 1 = 77. 77 ist durch 11 teilbar, also auch 781.
- Also, 781 ist nicht prim. Es ist mindestens durch 11 teilbar.
- Beispiel # 2. Lass uns 527 machen.
- Bleistift und Papier. Prüfen.
- Schätzen Sie die Quadratwurzel. 527 liegt zwischen 400 und 625. Wenn ich also meine Tabelle betrachte, ist die Quadratwurzel von 527 wahrscheinlich etwa 23. Also die Primzahlen, die ich testen muss, sind wieder 2 bis 23.
- Prüfen Sie die Teilbarkeit nach 2, 3, 5, 7, 11, 13, 17, 19 und 23.
- Um zwei: 527 endet nicht in 2, 4, 6 oder 8. So weit, so gut.
- Um drei: Füge die Ziffern hinzu; 5 + 2 + 7 = 14. 14 ist nicht durch 3 teilbar, also auch nicht 527.
- Um fünf: 527 endet nicht in 0 oder 5. Weiter geht's.
- Um sieben: Multiplizieren Sie die letzte Ziffer mit zwei; 2 * 7 = 14. Subtrahiere es von den restlichen Ziffern; 52 - 14 = 38. 38 ist nicht durch 7 teilbar, also auch nicht 527.
- Bis elf: Subtrahiere die letzte Ziffer von den restlichen Ziffern; 52 - 7 = 45. 45 ist nicht durch 11 teilbar, also auch nicht 527.
- Um dreizehn: Multiplizieren Sie die letzte Ziffer mit vier; 7 * 4 = 28. Fügen Sie auch die restlichen Ziffern hinzu; 52 + 28 = 80. 80 ist nicht durch 13 teilbar, also auch nicht 527.
- Um 17: Multiplizieren Sie die letzte Ziffer mit fünf; 7 * 5 = 35. Subtrahiere es von den restlichen Ziffern; 52 - 35 = 17. 17 ist durch 17 teilbar, also auch 527.
- Also, 527 ist nicht prim. Es ist mindestens durch 17 teilbar.
- Beispiel Lass uns 781 machen.
 Minotauromaquia
Minotauromaquia
 1 Besorge Bleistift und Papier. Wie bei jedem mathematischen Prinzip werden Sie sich besser daran erinnern, wenn Sie gleichzeitig auf dem Papier üben.
1 Besorge Bleistift und Papier. Wie bei jedem mathematischen Prinzip werden Sie sich besser daran erinnern, wenn Sie gleichzeitig auf dem Papier üben. 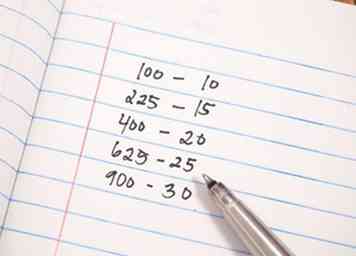 2 Schätzen Sie die Quadratwurzel der Zahl. Dies wird Ihre Prüfung beschleunigen, da nur versucht werden muss, die mögliche Primzahl durch die Primzahlen zu dividieren, die kleiner sind als die Quadratwurzel dieser Zahl. Ein kurzer Hinweis könnte helfen: Die Quadratwurzel von 100 ist 10, von 225 ist 15, von 400 ist 20, von 625 ist 25 und von 900 ist 30.
2 Schätzen Sie die Quadratwurzel der Zahl. Dies wird Ihre Prüfung beschleunigen, da nur versucht werden muss, die mögliche Primzahl durch die Primzahlen zu dividieren, die kleiner sind als die Quadratwurzel dieser Zahl. Ein kurzer Hinweis könnte helfen: Die Quadratwurzel von 100 ist 10, von 225 ist 15, von 400 ist 20, von 625 ist 25 und von 900 ist 30. 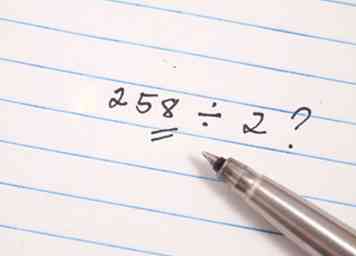 3 Erfahren Sie, wie Sie schnell erkennen können, ob eine Zahl durch 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 oder 31 teilbar ist. Da die Quadratwurzel von 1000 ungefähr 33 ist, müssen Sie nie eine Zahl höher als 31 testen. Indem Sie die Anzahl der Tests auf 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 verringern, und 31 hast du schon die halbe Miete gewonnen.
3 Erfahren Sie, wie Sie schnell erkennen können, ob eine Zahl durch 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 oder 31 teilbar ist. Da die Quadratwurzel von 1000 ungefähr 33 ist, müssen Sie nie eine Zahl höher als 31 testen. Indem Sie die Anzahl der Tests auf 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 verringern, und 31 hast du schon die halbe Miete gewonnen.  4 Versuchen Sie, die mögliche Primzahl durch Primzahlen zu dividieren, die kleiner als die Quadratwurzel dieser Zahl sind.
4 Versuchen Sie, die mögliche Primzahl durch Primzahlen zu dividieren, die kleiner als die Quadratwurzel dieser Zahl sind.  5 Mit einem selbstsicheren Grinsen proklamieren, ob es Prime ist und was es teilbar ist!
5 Mit einem selbstsicheren Grinsen proklamieren, ob es Prime ist und was es teilbar ist!