Euklid, in seinem berühmten 13 Buch Abhandlung über Geometrie, "Elemente", gibt in Buch I Proposition 2, die Lösung und Demonstration von, wie "Von einem gegebenen Punkt (A) eine rechte Linie gleich einer gegebenen endlichen rechten Linie (BC ) ". Dieser Artikel zeigt Ihnen, wie er die Lösung und Demonstration und somit den Beweis für das Problem erreicht hat. Außerdem wird die Verwendung der Excel-Medienbrowser-Werkzeugoption "Shapes" demonstriert, mit der ein geometrischer Proof simuliert werden kann.
Erster Teil von Drei:
Das Tutorial
-

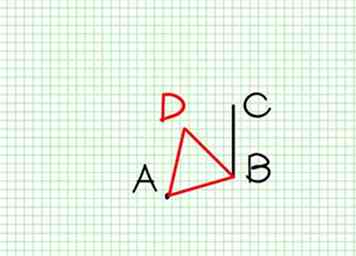
 1
1
Lösung --- Join AB (Post.I.); auf AB beschreiben das gleichseitige Dreieck ABD [I.1] - (siehe den Artikel, wie man eine Linie = zur Quadratwurzel von 3 geometrisch bestimmt, auf, wie man ein gleichseitiges Dreieck richtig baut, wenn Sie nicht wie wissen). Um dies mit dem Medienbrowser zu tun, folgen Sie den Unterschritten in diesen Bildern aus Excel und konvertiert über die Preview App in PNG-Dateien. -
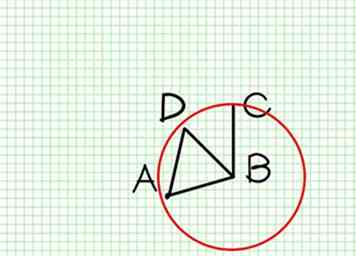 2 Mit B als Mittelpunkt und BC als Radius beschreiben Sie den Kreis ECH (Post. III.).
2 Mit B als Mittelpunkt und BC als Radius beschreiben Sie den Kreis ECH (Post. III.). -
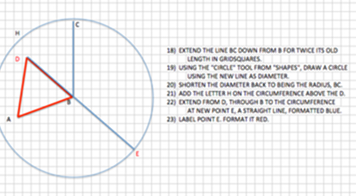
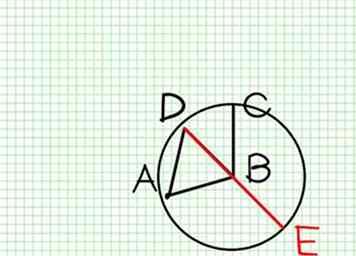 3 Produziere DB, um den Kreis ECH in E zu treffen (Post. II).
3 Produziere DB, um den Kreis ECH in E zu treffen (Post. II). -

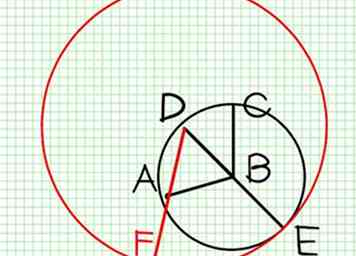 4 Mit D als Mittelpunkt und DE als Radius beschreiben Sie den Kreis EFG (Post. III.). Produziere DA, um diesen Kreis in AF zu treffen.
4 Mit D als Mittelpunkt und DE als Radius beschreiben Sie den Kreis EFG (Post. III.). Produziere DA, um diesen Kreis in AF zu treffen. -
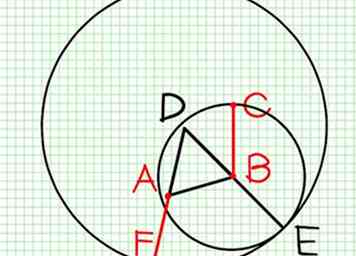 5 Erkenne, dass AF gleich BC ist.
5 Erkenne, dass AF gleich BC ist. -
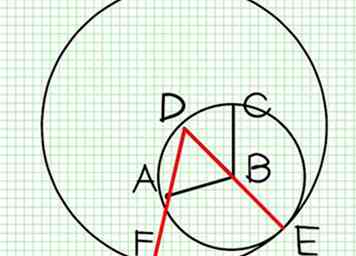 6 Demonstrieren --- Da D der Mittelpunkt des Kreises EFG ist, ist DF gleich DE (Def. XXXII.).
6 Demonstrieren --- Da D der Mittelpunkt des Kreises EFG ist, ist DF gleich DE (Def. XXXII.).
Zweiter Teil von Drei:
Erläuterungsdiagramme, Diagramme, Fotos
-
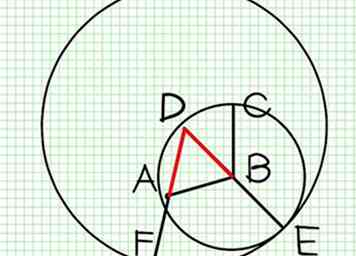 1 Da DAB ein gleichseitiges Dreieck ist, wissen Sie, dass DA gleich DB ist (Def. XXI.). Daher haben wir DF = DE und DA = DB; und die letztere von der ersteren nehmend, ist der Rest AF gleich dem Rest BE (Axiom III). Da B der Mittelpunkt des Kreises ECH ist, ist BC gleichbedeutend mit BE; und es ist bewiesen, dass AF gleich BE ist; und Dinge, die dem gleichen gleich sind, sind einander gleich (Axiom I.)
1 Da DAB ein gleichseitiges Dreieck ist, wissen Sie, dass DA gleich DB ist (Def. XXI.). Daher haben wir DF = DE und DA = DB; und die letztere von der ersteren nehmend, ist der Rest AF gleich dem Rest BE (Axiom III). Da B der Mittelpunkt des Kreises ECH ist, ist BC gleichbedeutend mit BE; und es ist bewiesen, dass AF gleich BE ist; und Dinge, die dem gleichen gleich sind, sind einander gleich (Axiom I.) -
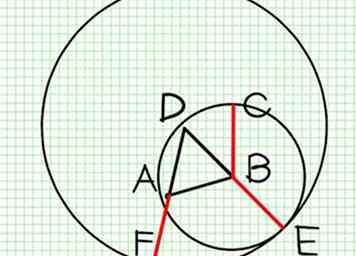 2 Daher ist AF gleich BC. Daher wurde von dem gegebenen Punkt A die Linie AF gleich der Linie BC gezeichnet.
2 Daher ist AF gleich BC. Daher wurde von dem gegebenen Punkt A die Linie AF gleich der Linie BC gezeichnet. -
 3 Es ist üblich mit Kommentatoren auf Euklid zu sagen, dass er die Verwendung der Regel und des Kompasses erlaubt. Wäre dies der Fall, wäre dieser Vorschlag unnötig gewesen. Tatsache ist, dass Euklids Ziel es war, theoretische und nicht praktische Geometrie zu lehren, und die einzigen Dinge, die er postuliert, sind das Zeichnen von geraden Linien und das Beschreiben von Kreisen. Wenn er den mechanischen Gebrauch der Regel und des Kompasses erlaubte, konnte er Methoden zur Lösung vieler Probleme geben, die über die Grenzen der "Geometrie des Punktes, der Linie und des Kreises" hinausgehen. Siehe Anmerkungen D, F am Ende dieser Arbeit (unter Bezugnahme auf Archives.org oder die Publikation der Royal University of Ireland). .
3 Es ist üblich mit Kommentatoren auf Euklid zu sagen, dass er die Verwendung der Regel und des Kompasses erlaubt. Wäre dies der Fall, wäre dieser Vorschlag unnötig gewesen. Tatsache ist, dass Euklids Ziel es war, theoretische und nicht praktische Geometrie zu lehren, und die einzigen Dinge, die er postuliert, sind das Zeichnen von geraden Linien und das Beschreiben von Kreisen. Wenn er den mechanischen Gebrauch der Regel und des Kompasses erlaubte, konnte er Methoden zur Lösung vieler Probleme geben, die über die Grenzen der "Geometrie des Punktes, der Linie und des Kreises" hinausgehen. Siehe Anmerkungen D, F am Ende dieser Arbeit (unter Bezugnahme auf Archives.org oder die Publikation der Royal University of Ireland). .
Teil drei von drei:
Hilfreiche Anleitung
- 1 Verwenden Sie Hilfsartikel, wenn Sie dieses Tutorial durcharbeiten:
- Eine Liste von Artikeln zu Excel, Geometrischer und / oder Trigonometrischer Kunst, Diagrammerstellung und algebraischer Formulierung finden Sie im Artikel Erstellen eines spiralförmigen Spinpartikel-Pfads oder einer Kettenform oder eines sphärischen Rahmens.
- Für weitere Diagramme und Diagramme, klicken Sie auf Kategorie: Microsoft Excel Bilder, Kategorie: Mathematik, Kategorie: Tabellenkalkulation oder Kategorie: Grafiken, um viele Excel Arbeitsblätter und Diagramme zu sehen, in denen Trigonometrie, Geometrie und Kalkül in Kunst umgewandelt wurden, oder klicken Sie einfach auf die Kategorie wie oben rechts auf der Seite oder links unten auf der Seite.
 Minotauromaquia
Minotauromaquia

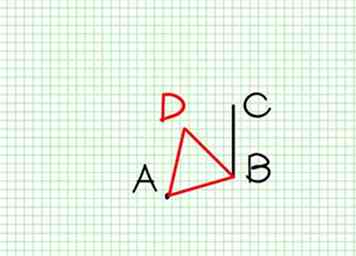
 1
1  2 Mit B als Mittelpunkt und BC als Radius beschreiben Sie den Kreis ECH (Post. III.).
2 Mit B als Mittelpunkt und BC als Radius beschreiben Sie den Kreis ECH (Post. III.). 
 3 Produziere DB, um den Kreis ECH in E zu treffen (Post. II).
3 Produziere DB, um den Kreis ECH in E zu treffen (Post. II). 
 4 Mit D als Mittelpunkt und DE als Radius beschreiben Sie den Kreis EFG (Post. III.). Produziere DA, um diesen Kreis in AF zu treffen.
4 Mit D als Mittelpunkt und DE als Radius beschreiben Sie den Kreis EFG (Post. III.). Produziere DA, um diesen Kreis in AF zu treffen.  5 Erkenne, dass AF gleich BC ist.
5 Erkenne, dass AF gleich BC ist.  6 Demonstrieren --- Da D der Mittelpunkt des Kreises EFG ist, ist DF gleich DE (Def. XXXII.).
6 Demonstrieren --- Da D der Mittelpunkt des Kreises EFG ist, ist DF gleich DE (Def. XXXII.).  1 Da DAB ein gleichseitiges Dreieck ist, wissen Sie, dass DA gleich DB ist (Def. XXI.). Daher haben wir DF = DE und DA = DB; und die letztere von der ersteren nehmend, ist der Rest AF gleich dem Rest BE (Axiom III). Da B der Mittelpunkt des Kreises ECH ist, ist BC gleichbedeutend mit BE; und es ist bewiesen, dass AF gleich BE ist; und Dinge, die dem gleichen gleich sind, sind einander gleich (Axiom I.)
1 Da DAB ein gleichseitiges Dreieck ist, wissen Sie, dass DA gleich DB ist (Def. XXI.). Daher haben wir DF = DE und DA = DB; und die letztere von der ersteren nehmend, ist der Rest AF gleich dem Rest BE (Axiom III). Da B der Mittelpunkt des Kreises ECH ist, ist BC gleichbedeutend mit BE; und es ist bewiesen, dass AF gleich BE ist; und Dinge, die dem gleichen gleich sind, sind einander gleich (Axiom I.)  2 Daher ist AF gleich BC. Daher wurde von dem gegebenen Punkt A die Linie AF gleich der Linie BC gezeichnet.
2 Daher ist AF gleich BC. Daher wurde von dem gegebenen Punkt A die Linie AF gleich der Linie BC gezeichnet.  3 Es ist üblich mit Kommentatoren auf Euklid zu sagen, dass er die Verwendung der Regel und des Kompasses erlaubt. Wäre dies der Fall, wäre dieser Vorschlag unnötig gewesen. Tatsache ist, dass Euklids Ziel es war, theoretische und nicht praktische Geometrie zu lehren, und die einzigen Dinge, die er postuliert, sind das Zeichnen von geraden Linien und das Beschreiben von Kreisen. Wenn er den mechanischen Gebrauch der Regel und des Kompasses erlaubte, konnte er Methoden zur Lösung vieler Probleme geben, die über die Grenzen der "Geometrie des Punktes, der Linie und des Kreises" hinausgehen. Siehe Anmerkungen D, F am Ende dieser Arbeit (unter Bezugnahme auf Archives.org oder die Publikation der Royal University of Ireland). .
3 Es ist üblich mit Kommentatoren auf Euklid zu sagen, dass er die Verwendung der Regel und des Kompasses erlaubt. Wäre dies der Fall, wäre dieser Vorschlag unnötig gewesen. Tatsache ist, dass Euklids Ziel es war, theoretische und nicht praktische Geometrie zu lehren, und die einzigen Dinge, die er postuliert, sind das Zeichnen von geraden Linien und das Beschreiben von Kreisen. Wenn er den mechanischen Gebrauch der Regel und des Kompasses erlaubte, konnte er Methoden zur Lösung vieler Probleme geben, die über die Grenzen der "Geometrie des Punktes, der Linie und des Kreises" hinausgehen. Siehe Anmerkungen D, F am Ende dieser Arbeit (unter Bezugnahme auf Archives.org oder die Publikation der Royal University of Ireland). .